Institutul de Matematică şi Informatică "Vladimir Andrunachievici"
Universitatea de Stat din MoldovaRO EN
Lie algebras of operators and invariant GL(2, ℜ)-integrals for Darboux type differential systems.
Authors: Diaconescu Oxana, Popa Mihail
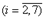degree with respect to the phase variables are considered. For every such system the admitted Lie algebra is constructed. With the aid of these algebras particular invariant GL(2, ℜ) -integrals as well as first integrals of considered systems are constructed. These integrals represent the algebraic curves of the (i-1)th 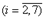degree. It is showed that the Darboux type systems with nonlinearities of the 2nd, the 4th and the 6th degree with respect to the phase variables do not have limit cycles.
– 0.16 Mb
Abstract
In this article two-dimensional autonomous Darboux type differential systems with nonlinearities of the ith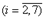 degree with respect to the phase variables are considered. For every such system the admitted Lie algebra is constructed. With the aid of these algebras particular invariant GL(2, ℜ) -integrals as well as first integrals of considered systems are constructed. These integrals represent the algebraic curves of the (i-1)th 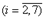degree. It is showed that the Darboux type systems with nonlinearities of the 2nd, the 4th and the 6th degree with respect to the phase variables do not have limit cycles.
E-mails: ,
Fulltext
– 0.16 Mb
Contents
- Lie algebras of operators and invariant GL(2, ℜ)-integrals for Darboux type differential systems.
- Measure of stability for a finite cooperative game with a generalized concept of equilibrium.
- Collocation and Quadrature Methods for Solving Singular Integral Equations with Piecewise Continuous Coefficients.
- Criterion of parametrical completeness in the 6-element non-chain extension of Intuitionistic logic of A. Heyting.
- Linear stability bounds in a convection problem for variable gravity field.
- A new method for computing the number of n-quasigroups.
- The GL(2, ℜ)-orbits of polynomial differential systems of degree four.
- A Linear Parametrical Programming Approach for Studying and Solving Bilinear Programming Problem.
- On topological torsion LCA groups with commutative ring of continuous endomorphisms.
- Natural classes and torsion free classes in categories of modules.
- Finite difference schemes for problems of mixture of two component elastic materials.
- Characteristic functions of Markovian random evolutions in ℜm.
- Nearly simple elementary divisor domains.
- Factorization theorems for some spaces of analytic functions.
