Sustinerea tezei de doctor
Se anunţă susţinerea tezei de doctor în științe matematice:
Pretendent: Alioşcenco Svetlana, lector superior universitar, Universitatea Transnistreană "Şevcenco T. G."
Conducător ştiinţific: Arnautov Vladimir, academician AŞM, profesor universitar, Institutul de Matematică şi Informatică al AŞM
Tema tezei: "Izomorfismul semiizometric al inelelor pseudonormate şi proprietăţile lui"
Specialitatea: 111.03 – Logică matematică, algebră şi teoria numerelor
Data: 17 mai 2016
Ora: 14:00
Local: Institutul de Matematică şi Informatică al Academiei de Ştiinţe a Moldovei (of. 340), str. Academiei 5, Chişinău, MD-2028, Republica Moldova.Consiliul ştiinţific specializat: D 01. 111.03 - 07 din cadrul Institutului de Matematică şi Informatică al AŞM
Membrii:- Reabuhin Iurie, preşedinte, doctor habilitat în ştiinţe fizico-matematice, profesor universitar, academician al AŞM, IMI.
- Izbaş Vladimir, secretar ştiinţific, doctor în ştiinţe fizico-matematice, conferenţiar cercetător, IMI.
- Chiriac Liubomir, doctor habilitat în ştiinţe fizico-matematice, profesor universitar, UST.
- Şcerbacov Victor, doctor habilitat în ştiinţe fizico-matematice, conferenţiar cercetător, IMI.
- Pavel Dorin, doctor în ştiinţe fizico-matematice, conferenţiar universitar, UST.
Referenți științifici oficiali:
- Cioban Mitrofan, doctor habilitat în stiinţe fizico-matematice, professor universitar, academician al AŞM., UST.
- Popa Valeriu, doctor în stiinţe fizico-matematice, conferenţiar universitar, IMI.
Principalele publicaţii ştiinţifice la tema tezei ale autorului:
- Aleschenko S. A., Arnautov V. I. Quotient rings of pseudonormed rings. Buletinul Academiei de Ştiinţe a Republicii Moldova, 2006, V. 1(44), p. 3 – 16.
- Aleschenko S. A., Arnautov V. I. Properties of one-sided ideals of pseudonormed rings when taking the quotient rings. Buletinul Academiei de Ştiinţe a Republicii Moldova, 2008, V. 3(58), p. 3 – 8.
- Aleschenko S. A semi-isometric isomorphism on a ring of matrices. Buletinul Academiei de Ştiinţe a Republicii Moldova, 2014, V. 2(75), p. 74 – 84.
- Алещенко С. А. Конструкции псевдонормированных колец, сохраняющие полуизометрический изоморфизм. În: Studia Universitatis Moldaviae. Ştiinţe Exacte şi Economice, 2013, т. 67, № 7, с. 19–27.
- Алещенко С. А. Некоторые конструкции псевдонормированных колец. В: Вестник науки Приднестровья, 2012, № 2, с. 147–155.
Rezumatul tezei
Problematica abordată. În teză este abordată problema identificării claselor de izomorfisme ale inelelor pseudonormate pentru care există analoage ale celei de a doua teoreme de izomorfism. În teză sunt considerate izomorfismele semiizometrice (semiizometrice la stânga, semiizometrice la dreapta) de inele pseudonormate, analoagele celei de a doua teoreme de izomorfism pentru inelele pseudonormate, construcţiile cu inele pseudonormate care păstrează aceste izomorfisme.
Conţinutul de bază al tezei. Teza constă din introducere, trei capitole, concluzii generale şi recomandări, bibliografie din 85 titluri, 127 pagini de text de bază. Rezultatele principale ale tezei au fost publicate în 15 lucrări ştiinţifice: 5 articole şi 10 comunicări la conferinţe ştiinţifice. În primul capitol al tezei se face o trecere în revistă a lucrărilor ştiinţifice în domeniul cercetării omomorfismelor şi izomorfismelor inelelor topologice. In capitolul doi se defineşte conceptele de izomorfism semiizometric (semiizometric la stânga, semiizometric la dreapta), se studiază analoagele teoremei de izomorfism pentru inelele pseudonormate. În capitolul trei se demonstrează teoremele despre păstrarea izomorfismului semiizometric bilateral şi unilateral pentru unele construcţii cu inele pseudonormate.
Principalele rezultate obţinute:
- Un izomorfismul de inele
 este izomorfism semiizometric dacă şi numai dacă pentru orice
este izomorfism semiizometric dacă şi numai dacă pentru orice 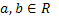 sunt îndeplinite inegalităţile
sunt îndeplinite inegalităţile 
 şi
şi  ;
; -
Un izomorfismul de inele
 este restricţie a unui omomorfism izometric de inele pseudonormate la un subinel accesibil de treaptă cel mult
este restricţie a unui omomorfism izometric de inele pseudonormate la un subinel accesibil de treaptă cel mult 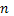 dacă şi numai dacă
dacă şi numai dacă 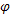 este o superpoziţie a
este o superpoziţie a 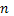 izomorfisme semiizometrice;
izomorfisme semiizometrice;
-
Dacă
 este un izomorfism semiizometric, iar
este un izomorfism semiizometric, iar 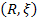 are un element care nu este divizor generalizat al lui zero, atunci izomorfismul
are un element care nu este divizor generalizat al lui zero, atunci izomorfismul 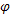 poate fi prelungit până la un izomorfism semiizometric
poate fi prelungit până la un izomorfism semiizometric  , unde
, unde 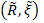 şi
şi  sunt completatele inelelor pseudonormate
sunt completatele inelelor pseudonormate 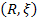 şi
şi  , respectiv;
, respectiv;
-
Dacă
 este un izomorfism semiizometric pentru fiecare
este un izomorfism semiizometric pentru fiecare  , atunci pentru orice
, atunci pentru orice  izomorfismul
izomorfismul  este semiizomorfic, unde
este semiizomorfic, unde  )),
)),  şi
şi