Institutul de Matematică şi Informatică "Vladimir Andrunachievici"
Universitatea de Stat din MoldovaRO EN
An approximate solution of the Fredholm type equation of the second kind for any λ ≠ 0
Authors: Alexander Kouleshoff
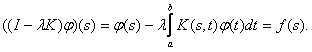
Assume that the complex-valued kernel K(s,t) is defined on
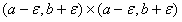for some ε > 0 and
, 
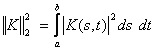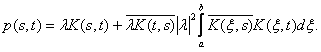
Consider the following mapping
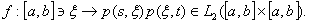
If the function f is integrable according to definition of the Riemann integral (as the function with values in the space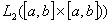
, then the kernel of the square of the integral operator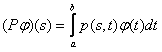 
can be approximated by a finite dimensional kernel. The formula (I - P)+ = (I - P2)+(I + P) and the persistency of the operator (I - P2)+ with respect to perturbations of special type are proved. For any λ≠0 we find approximations of the function φ which minimizes functional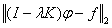
and has the least norm in L2[a, b] among all functions minimizing the above mentioned functional. Simultaneously we find approximations of the kernel and orthocomplement to the image of the operator I - λK if λ≠0 is a characteristic number.
The corresponding approximation errors are obtained.
– 0.17 Mb
Abstract
Consider the following equation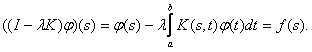Assume that the complex-valued kernel K(s,t) is defined on
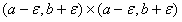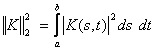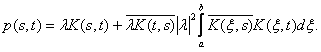
for some ε > 0 and, Consider the following mapping
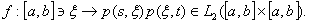
If the function f is integrable according to definition of the Riemann integral (as the function with values in the space
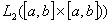, then the kernel of the square of the integral operator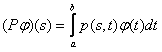 can be approximated by a finite dimensional kernel. The formula (I - P)+ = (I - P2)+(I + P) and the persistency of the operator (I - P2)+ with respect to perturbations of special type are proved. For any λ≠0 we find approximations of the function φ which minimizes functional
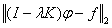and has the least norm in L2[a, b] among all functions minimizing the above mentioned functional. Simultaneously we find approximations of the kernel and orthocomplement to the image of the operator I - λK if λ≠0 is a characteristic number.
The corresponding approximation errors are obtained.
E-mail: ;
Fulltext
– 0.17 Mb
Contents
- On orthogonality of binary operations and squares.
- On the lattice of closed classes of modules.
- Lie algebras of the operators and three-dimensional polynomial differential systems.
- On a Functional Equation with a Group Isotopy Property.
- Left exact radicals in module categories over principal ideal domains.
- An approximate solution of the Fredholm type equation of the second kind for any λ ≠ 0
- On a criterion of normality for mappings.
- Strong Stability of Linear Symplectic Actions and the Orbit Method.
