Examenul de bacalaureat la matematica, 2000
Profilurile: fizica-matematica, economie, informatica-matematica
1. Stabiliti carei multimi de numere ii apartine valoarea expresiei
(5 puncte)
2. Fie functiile f : R ®
R, f(x) = x2 - 3x + 2; g :
R ® R, g(x) = 2x -
3. Determinati f(g(x)).
3. Determinati valorile parametrului real a pentru care
ecuatia 
admite
radacini. (6 puncte)
4. Determinati lungimea liniei definita de ecuatia x2 + 5x + y2 = 0. (7 puncte)
5. Rezolvati inecuatia D(x) ≥ 0, unde
| D(x) = |
|
6. Determinati exponentul puterii la care trebuie ridicat
folosind formula binomului, astfel incat
(8 puncte)
7. Calculati integrala
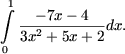
8. Centrul cercului inscris intr-un triunghi isoscel imparte inaltimea lui in segmente de lungime, respectiv de, 5 cm si 3 cm. Aflati lungimile laturilor triunghiului. (9 puncte)
9. Sa se determine pentru ce valori ale parametrului real m
functia f : R ® R,
10. Descompuneti in factori ireductibili polinomul P(X)
= X 4 + 13X 2 + 36 peste multimea C.
11. Aria sectiunii diagonale a unei piramide patrulatere regulate este S. O muchie laterala a ei formeaza cu planul bazei piramidei un unghi de masura b. Aflati volumul piramidei. (12 puncte)
12. Determinati toate valorile parametrului real a, pentru care sistemul:
1. Se observa ca
si se obtine
Nota: N Ì Z Ì Q Ì R Ì C ... (a se vedea si sesiunea 1999).
2. Se utilizeaza definitia functiei compuse si se obtine
3. Ecuatia asinx + bcosx = c are
solutii daca si numai daca 
(a se vedea Ecuatii
trigonimetrice, metoda unghiului auxiliar). Prin urmare, ecuatia data
are solutii doar pentru 
de unde a Î [-2,2].
4. Cum 
rezulta ca linia data este o circumferinta de raza
cu centrul in
punctul M
.
Se aplica formula pentru determinarea lungimii circumferintei si se obtine
= 5p(un.lungime).
5. Se utilizeaza proprietatile determinantilor si se obtine
| D(x) = |
|
= |
|
= (2x - 1) |
|
= |
| = 2(x - 1) |
|
= (2x - 1)(x + 1)2 |
|
= (2x - 1)(x + 1)2. |
Inecuatia D(x) ≥ 0 devine (2x - 1)(x +
1)2 ≥ 0. Se rezolva utilizand metoda intervalelor
si se obtine x Î
{-1}È[1/2;+¥).
6. Se utilizeaza formula pentru termenul de rang k din dezvoltarea binomului lui Newton (a + b)n:
7. Cum integrantul reprezinta o functie rationala, il descompunem in fractii simple (tinand seama ca radacinile trinomului din numitor sunt reale si de multiplicitatea unu):
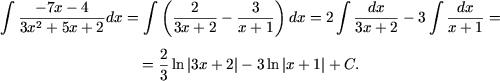
Conform formulei Newton-Leibniz
8. Fie ABC - tringhiul isoscel (AB = BC),
BD - inaltimea (BD^AC)
O Î BD - centrul cercului inscris in
DABC, OB = 5 cm, OD = 3 cm, si
prin urmare BD = 8(cm). Fie E - punctul de tangenta a laturii
AB cu cercul. Atunci OE^AB si
prin urmare DBOE - dreptunghic. Cum
OE = OD = 3,
Cum triunghiurile dreptunghice BOE si ABD sunt asemenea (ÐB - comun), rezulta:
Cum BD - inaltimea coborata pe baza tringhiului isoscel ABC,
rezulta BD - mediana si
Asadar AB = BC = 10cm, AC = 12cm.
9. Functia f : X ® R,
X Ì R este
monoton descrescatoare pe X daca
f ¢(x) ≤ 0 pentru orice
Cum ex > 0 pentru orice x Î R, inecuatia devine
Asadar: 25 - 4(3 - m) ≤ 0, de unde
10. Se considera ecuatia bipatrata
11.
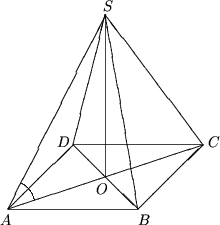
Fie SABCD - piramida patrulaterala regulata (ABCD - patrat),
aria DSAC = S,
ÐSAC =
b,
Prin urmare
AB2 = a2 + a2 =
2a2 = 2Sctgb (aria bazei
piramidei), 
(inaltimea piramidei) si
12. Din prima ecuatie a sistemului rezulta y = x si
x > 0 (expresia 
este definita doar pentru
 |
a2 - a - 2 < 0, | ||
|
Asadar, a Î
{-2}È[-1,2).