Экзамен по математике на соискание звания бакалавра, 2000
Профиль: физика-математика, экономика, информатика-математика
1. Определить, какому числовому множеству принадлежит значение
выражения
(5 очков)
2. Пусть даны функции f : R ®
R, f(x) = x2 - 3x + 2; g :
R ® R, g(x) =
2x - 3.
Найдите
3. При каких значениях действительного параметра a уравнение
имеет
решения? (6 очков)
4. Вычислить длину кривой x2 + 5x + y2 = 0. (7 очков)
5. Решить неравенство D(x) ≥ 0 где
| D(x) = |
|
6. Определить показатель степени, в котором нужно возвести
используя формулу бинома Ньютона, так чтобы
(8 очков)
7. Вычислить интеграл
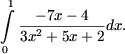
8. Центр вписанной в равнобедренный треугольник окружности делит его высоту на отрезки длины 5 см и 3 см. Найдите длины сторон треугольника. (9 очков)
9. При каких значениях действительного параметра m,
функция f : R ® R,
10. Разложить на простые множители в C многочлен P(X) = X 4 + 13X 2 + 36. (9 очков)
11. Площадь диагонального сечения правильной прямоугольной пирамиды равна S. Боковое ребро пирамиды образует с плоскостью основания угол b. Найдите объем пирамиды. (12 очков)
12. При каких значениях действительного параметра a, система
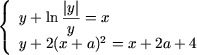
1. Заметим, что
и получим
Замечание: N М Z М Q М R М C ... (см. и варианты 1999 года).
2. Используя определение сложной функции получим
3. Уравнение asinx + bcosx = c
имеет решения если и только если
(следует из метода вспомогательного угла). Следовательно, данное уравнение
имеет решения лишь при
откуда a
О [-2,2].
4. Так как
то данная кривая есть окружность радиуса
с центром в точке
M
.
Используя формулу для определения длины окружности, получим
= 5p(ед.длины).
5. Используя свойство определителей, получим
| D(x) = |
|
= |
|
= (2x - 1) |
|
= |
| = 2(x - 1) |
|
= (2x - 1)(x + 1)2 |
|
= (2x - 1)(x + 1)2. |
Неравенство D(x) ≥ 0 примет вид (2x - 1)(x +
1)2 ≥ 0. Используя метод интервалов
получим x О
{-1}И[1/2;+Ґ).
6. Используя формулу для k-го слагаемого в разложении бинома Ньютона (a + b)n:
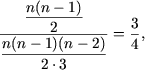
7. Подинтегральная функция есть дробно-рациональная функция. Учитывая что корни трехчлена знаменателя есть действительные числа кратности один, разложим функцию на простые дроби
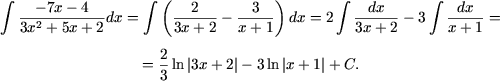
Согласно формуле Ньютона-Лейбница
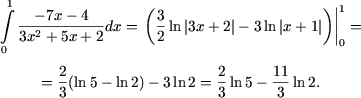
8. Пусть ABC - равнобедренный треугольник
(AB = BC), BD - высота
(BD^AC)
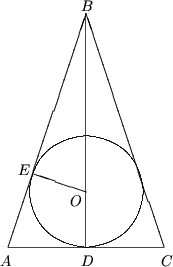
Так как прямоугольные треугольники BOE и ABD подобны (РB - общий), то
Поскольку BD - высота опущенная на основание равнобедренного тркугольника ABC, то BD - медиана и AC = 2AD = 12(см).
Таким образом AB = BC = 10 см, AC = 12 см.
9. Функция f : X ® R, X М R монотонно убывает на X если f ў(x) ≤ 0 для любого x О X. Следовательно
Поскольку ex > 0 для любого x О R, неравенство примет вид
Следовательно: 25 - 4(3 - m) ≤ 0, откуда
10. Рассмотрим биквадратное уравнение
11.
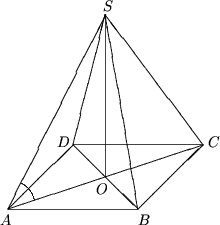
Пусть SABCD - правильная четырехугольная пирамида (ABCD
квадрат), площадь DSAC = S,
РSAC =
b, O - центр квадрата ABCD.
Пусть AO = a. Тогда AC = 2a;
Следовательно
AB2 = a2 + a2 =
2a2 = 2Sctgb (площадь
основания пирамиды),
(высота пирамиды) и
(куб.ед.)
12. Из первого уравнения системы следует y = x и
x > 0 (выражение 
определено лишь для y > 0 - см. Формулы, Словари,
Модуль). Тогда второе уравнение примет вид
 |
a2 - a - 2 < 0, | ||
|
Таким образом, a О
{-2}И[-1,2).