| Pagina principala | Ghidul utilizatorului | Rubrica candidatului | Curriculumurile scolare |
| Matematica competitiva | Matematica distractiva| Formule, dictionare | Avizuri |
|Pagini din istorie | Examene, teste | Bibliografie | Link-uri | Site map |

Metoda principala de rezolvare a inecuatiilor trigonometrice consta in reducerea lor la inecuatii de forma

sinx Ú a,     cosx Ú a,     tgx Ú a,     ctgx Ú a,

(1)

unde a Î R, semnul "Ú" desemneaza semnul compararii si inlocuieste oricare din semnele ">",   " ³ ",   "<",  " £" si utilizarea afirmatiilor ce urmeaza.

Afirmatia 1. Multimea solutiilor inecuatiei

sinx > a

(2)

este

1. R, daca a < -1;
2. (arcsina + 2pk; p - arcsina + 2pk), daca -1 £ a < 1;
3. Multimea vida, daca a ³ 1.

Afirmatia 2. Multimea solutiilor inecuatiei

sinx < a

(3)

este

1. R, daca a > 1;
2. (-p - arcsina + 2pk; arcsina + 2pk), daca -1 < a £ 1;
3. Multimea vida, daca a £ -1.

Afirmatia 3. Multimea solutiilor inecuatiei

cosx > a

(4)

este

1. R, daca a < -1;
2. (2pk - arccosa; 2pk + arccosa), daca -1 £ a < 1;
3. Multimea vida, daca a ³ 1.

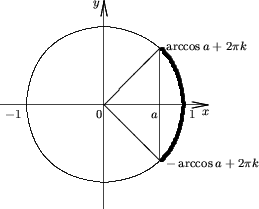
Afirmatia 4. Multimea solutiilor inecuatiei

cosx < av

(5)

este

1. R, daca a > 1;
2. (2pk + arccosa; 2p(k + 1) - arccosa), daca -1 < a £ 1;
3. Multimea vida, daca a £ -1.

Afirmatia 5. Multimea solutiilor inecuatiei

tgx > a

(6)

este

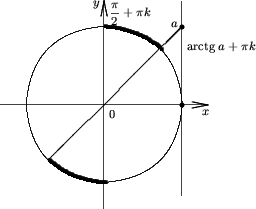
Afirmatia 6. Multimea solutiilor inecuatiei

tgx < a

(7)

este

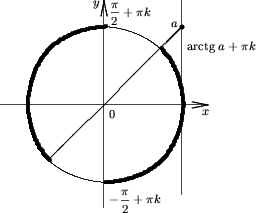
Afirmatia 7. Multimea solutiilor inecuatiei

ctgx > a

(8)

este (pk; arcctga + pk).

Afirmatia 8. Multimea solutiilor inecuatiei

ctgx < a

(9)

este (arcctga + pk; p(k + 1))

Nota. 1. Daca semnul inegalitatii in (2 )-(9 ) nu este strict, in multimea solutiilor inecuatiilor se includ si solutiile ecuatiei respective.

2. Afirmatiile 1-8 se obtin nemijlocit analizand graficul functiilor trigonometrice respective.

Exemplul 1. Sa se rezolve inecuatiile

1)	7) ctg2x - ctgx - 2 £ 0;
2)	8)
3)	9)
4) -2 £ tgx < 1;	10) 4sinxcosx(cos2x - sin2x) < sin6x;
5) 2sin2x - 5sinx + 2 > 0;	11) sinxsin3x ³ sin5xsin7x;
6)	12) sinx + sin2x + sin3x > 0.

Rezolvare. 1) Se noteaza 2x = t si se obtine inecuatia sint < ¹/₂ care, conform afirmatiei 2 are solutiile

Asadar, solutiile inecuatiei enuntate formeaza multimea

2) Cum functia sinus este impara,

3) Cum inecuatia devine sau Se aplica afirmatia 3 si se obtine

Altfel,

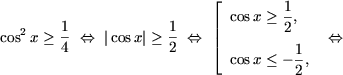
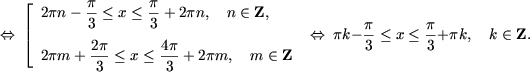
4) Se aplica afirmatiile 5 si 6 si se obtine

-2 £ tgx < 1   Û

tgx < 1, tgx ³ -2,

Û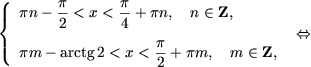

5) Se noteaza t = sinx si se obtine inecuatia de gradul al doilea

	t < 1/2,
	t > 2,

	sinx > 2,
	sinx < 1/2.

6) Cum

7) Se noteaza t = ctgx si se obtine inecuatia patrata

-1 £ ctgx £ 2   Û

ctgx £ 2, ctgx ³ -1,

Û

pk + arcctg2 £ x < p + pn,     n Î Z

Û

8) Se utilizeaza metoda unghiului auxiliar si se obtine

9) Se noteaza tgx = t si se rezolva inecuatia in t utilizand metoda intervalelor:

Asadar, se obtine totalitatea de inecuatii

	0 < tgx £ 1,
	tgx < -1,

0 < tgx £ 1, tgx < -1,

Û

tgx £ 1, tgx > 0,

Û

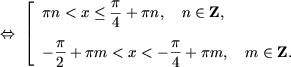
10) Se utilizeaza formulele sinusului si cosinusului argumentului dublu si se obtine

Se tine seama ca 2p este o perioada a functiei f(x) = sinxcos5x si se utilizeaza metoda generalizata a intervalelor pentru un interval de lungime 2p:

Astfel multimea solutiilor inecuatiei date este reuniunea multimilor

11) sinxsin3x ³ sin2xsin4x   Û   ¹/₂(cos2x - cos4x) ³ ¹/₂(cos2x - cos6x)   Û   -cos4x ³ -cos6x   Û   cos6x - cos4x ³ 0   Û   -2sinxsin5x ³ 0   Û   sinxsin5x £ 0.

Ultima inecuatie se rezolva similar exemplului precedent si se obtine multimea solutiilor

12) sinx + sin2x + sin3x > 0   Û   (sinx + sin3x) + sin2x > 0   Û   2sin2xcosx + sin2x > 0   Û

Û   sin2x(2cosx + 1) > 0   Û

sin2x > 0, cosx > -1/2, sin2x < 0, cosx < -1/2,

Û

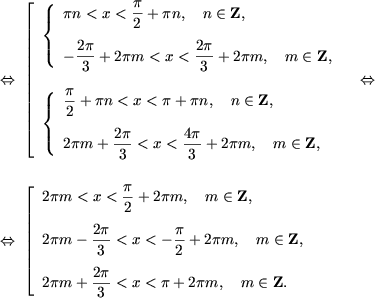
Sa se rezolve inecuatiile:

1. tg³x + tg²x - tgx - 1 > 0;

2. tgx + ctgx £ 2;

3. sin2x < cosx;

4. cosx + cos2x + cos3x ³ 0;

5. 6sin²x - 5sinx + 1 > 0;

6. 

7. 

8. 

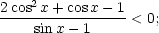
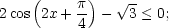
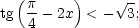
9. 2sin²x + 9cosx - 6 ³ 0;

10. 

11. 

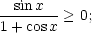
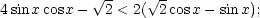
12. cos2x + sinx ³ 0.

| Pagina principala | Ghidul utilizatorului | Rubrica candidatului | Curriculumurile scolare |
| Matematica competitiva | Matematica distractiva| Formule, dictionare | Avizuri |
|Pagini din istorie | Examene, teste | Bibliografie | Link-uri | Site map |

---