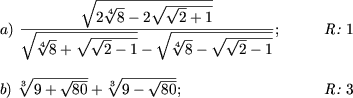Definitie. Vom numi expresie algebrica expresia, ce se obtine din constante si variabile prin intermediul operatiilor de adunare, scadere, inmultire, impartire, ridicare la o putere intreaga si extragerea radacinii.
Exemple de expresii algebrice:
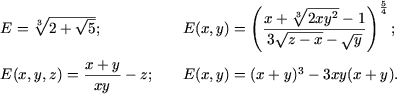
Definitie. Domeniu al valorilor admisibile (concis DVA) al expresiei algebrice E(x1, x2, ..., xn) (D(E)) se numeste multimea tuturor cortegiilor (x1, x2, ..., xn) pentru care expresia E(x1, x2, ..., xn) are sens.
De exemplu, DVA al expresiei
![]() este multimea
D(E) = {(x,y) |
x Î R,
y Î R,
xy ¹ 0}, iar DVA al
expresiei
este multimea
D(E) = {(x,y) |
x Î R,
y Î R,
xy ¹ 0}, iar DVA al
expresiei ![]() este multimea
tripletelor {(x,y,z) |
x, y, z Î R,
xy ³ 0}.
este multimea
tripletelor {(x,y,z) |
x, y, z Î R,
xy ³ 0}.
Definitie. Expresiile algebrice E1 si E2 se numesc identic egale pe multimea M Ì D(E1)ÇD(E2), daca valorile numerice ale acestor expresii sunt egale pentru orice valori ale variabilelor din M.
De exemplu ![]() pe multimea
[0;+¥),
pe multimea
[0;+¥),
![]() pe multimea
(-¥;0],
pe multimea
(-¥;0],
![]() pe multimea R\{-1},
(x + y)2 = x2 +
2xy + y2 pe multimea
{(x,y) | x Î R,
y Î R}.
pe multimea R\{-1},
(x + y)2 = x2 +
2xy + y2 pe multimea
{(x,y) | x Î R,
y Î R}.
Definitie. Vom numi transformare identica a expresiei algebrice pe multimea M Í D(E) inlocuirea acestei expresii cu o expresie identic egala cu ea.
Nota. Tinem sa mentionam, ca uneori multimea M pe care expresiile algebrice sunt identic egale nu se evidentiaza, avandu-se in vedere egalitatea identica a acestor expresii pe intersectia domeniilor lor de definitie.
De exemplu
In procesul transformarilor identice sunt utile urmatoarele formule:
- 1.
- (a ± b)2 = a2 ± 2ab + b2,
- 2.
- (a ± b)3 = a3 ± 3a2b + 3ab2 ± b3,
- 3.
- a2 - b2 = (a - b)(a + b),
- 4.
- a3 ± b3 =
(a ±
b)(a2
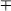 ab + b2).
ab + b2).
Aceste formule se obtin ca consecinte ale urmatoarelor formule generale:
- 5.
- an - bn = (a - b)(an-1 + an-2b + ... + abn-2 + bn-1) (n Î N),
- 6.
- a2n+1 + b2n+1 = (a + b)(a2n - a2n-1b + ... - ab2n-1 + b2n) (n Î N),
- 7.
- (binomul lui Newton)
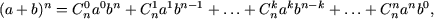
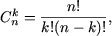 n! = 1·2·3·...·n, 0! = 1.
n! = 1·2·3·...·n, 0! = 1.
Egalitatile ce urmeaza sunt juste pentru orice numere pozitive a si b si orice numere reale a si b.
- a0 = 1;
- aa + b =
aa · ab;
-
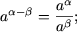
- (aa)b = aab;
- (ab)a =
aa · ba;
-
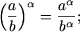
-
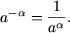
Nota 1. Tinem sa mentionam, ca numerele negative la fel pot fi ridicate
la anumite puteri (intregi, sau mai general, rationale de tipul
![]() unde m - intreg,
unde m - intreg,
Nota 2. 0a = 0, pentru orice a > 0.
-
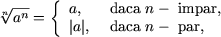
-
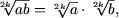 daca a
³ 0, b ³ 0,
k Î N,
daca a
³ 0, b ³ 0,
k Î N,
-
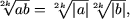 daca ab
³ 0, k Î N.
daca ab
³ 0, k Î N.
-
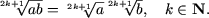
-
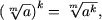 a ³ 0, daca m este par, a
Î R daca m este impar.
a ³ 0, daca m este par, a
Î R daca m este impar.
-
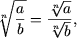 daca a ³ 0, b > 0,
n - par sau b ¹ 0,
a Î R, daca n - impar.
daca a ³ 0, b > 0,
n - par sau b ¹ 0,
a Î R, daca n - impar.
-
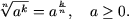
-
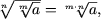 a ³ 0 daca m par sau n par,
a Î R daca m·n - impar.
a ³ 0 daca m par sau n par,
a Î R daca m·n - impar.
-
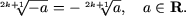
-
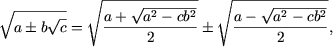 unde a > 0,
b > 0, c > 0 si a2
³ b2c.
unde a > 0,
b > 0, c > 0 si a2
³ b2c.
Exemplul 1. Sa se determine DVA al expresiilor algebrice:
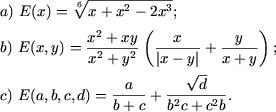
Rezolvare. a) DVA al expresiei enuntate se determina rezolvand inecuatia x + x2 - 2x3 ³ 0 cu ajutorul metodei intervalelor:
Asadar D(E) = (-¥;-1/2]È[0;1].
b) Se tine seama ca expresia are sens, daca
| x2 + y2 ¹ 0, | |
| |x - y| ¹ 0, | |
| x + y ¹ 0, |
c) Cum numitorii fractiilor rationale urmeaza a fi diferiti de zero, iar radacina de ordinul doi exista numai din expresii nenegative, se obtine sistemul
|
Û |
|
Û |
|
Asadar DVA al expresiei date este multimea {(a,b,c,d) | b + c ¹ 0, b ¹ 0, c ¹ 0, d ³ 0}.
Exemplul 2. Sa se determine daca expresiile A si B sunt identic egale pe multimea M.
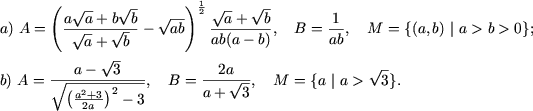
Rezolvare. a) Cum ![]()
![]()
![]()
![]() pe mulitmea M, se aplica formulele inmultirii prescurtate si se obtine:
pe mulitmea M, se aplica formulele inmultirii prescurtate si se obtine:
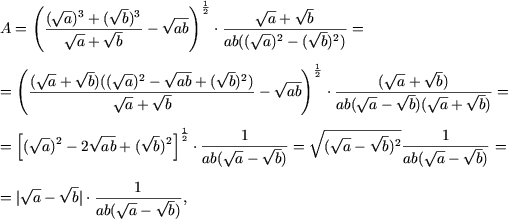
b) Similar exemplului precedent
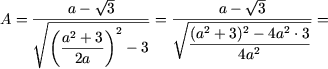
S-a tinut seama ca daca ![]() atunci
atunci ![]() si
si
![]()
Exemplul 3. Sa se aduca la o forma mai simpla expresiile:
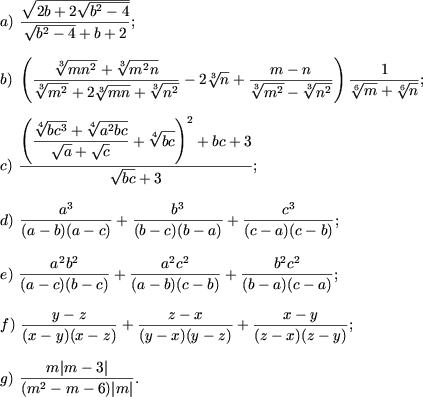
Rezolvare. DVA al expresiei se determina din sistemul
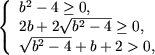 de unde rezulta b ³ 2.
de unde rezulta b ³ 2.
In DVA expresia este identic egala cu:
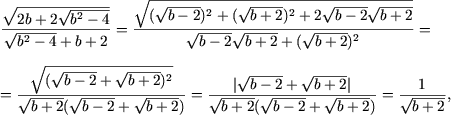
b) DVA al expresiei este multimea
{(m,n) | m ³ 0,
n ³ 0,
m ¹ n}. Se noteaza
![]()
![]() atunci
atunci
![]()
![]() m = a6 si
m = a6 si
![]()
![]() n = b6 si expresia devine
n = b6 si expresia devine

c) In DVA: {(a,b,c) | a ³ 0, b ³ 0, c ³ 0, a2 + c2 ¹ 0} expresia se tranforma astfel:
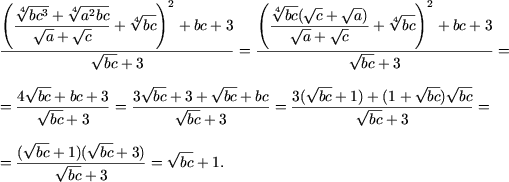
d) DVA al expresiei este multimea {(a,b,c) | a ¹ b, a ¹ c, b ¹ c}. Se aduce expresia la numitor comun si se obtine
Se tine seama de expresia de la numitor si se descompune in factori numaratorul
| a3(c - b) + b3(a - c) + c3(b - a) = c(a3 - b3) + ab(b2 - a2) + c3(b - a) = |
| = (a - b)(c(a2 + ab + b2) - ab(a + b) - c3) = (a - b)(c(a2 - c2) + ab(c - a) + b2(c - a)) = |
| = (b - c)(a - b)(-a2b - a2c + c2(a + b)) = (a - b)(b - c)(b(c2 - a2) + ac(c - a)) = |
| = (a - b)(b - c)(c - a)(ab + bc + ca). |
Asadar pe DVA expresia enuntata este identic egala cu ab + bc + ca.
f) DVA al expresiei este multimea {(x,y,z) | x ¹ y, y ¹ z, z ¹ x}. Primul termen al expresiei se descompune in modul urmator:
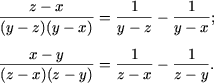
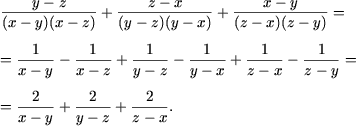
g) DVA al expresiei este R\{-2;0;3}. Se tine seama ca expresia contine |m| si |m - 3| si se considera urmatoarele trei cazuri:
- fie m Î
(-¥;-2)È(-2;0). Atunci
|m| = -m, |m - 3| = -(m - 3)
si expresia devine
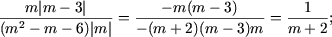
- fie m Î (0;3).
Atunci |m| = m, |m - 3| = -(m - 3)
si expresia devine
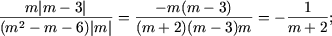
- fie m Î (3;+¥).
Atunci |m| = m, |m - 3| = m-3 si expresia devine
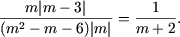
Asadar
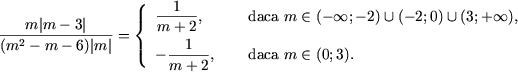
Exemplul 4. Sa se descompuna in factori
| a) (x + y)(y + z)(z + x) - xyz; |
| b) x3 + y3 + z3 - 3xyz; |
| c) x8 + x7 + x6 + x5 + x4 + x3 + x2 + x + 1; |
| d) x5 + x + 1. |
Rezolvare. a) Se aduna si se scade z(y + z)(z + x) si se grupeaza convenabil
| (x + y)(y + z)(z + x) + z(y + z)(z + x) - z(y + z)(z + x) - xyz = |
| = (y + z)(z + x)(x + y + z) - z((y + z)(z + x) - xy) = |
| = (y + z)(z + x)(x + y + z) - z(z2 + yz + zx) = |
| = (y + z)(z + x)(x + y + z) - z2(x + y + z) = |
| = (x + y + z)((y + z)(z + x) - z2) = (x + y + z)(xy + yz + zx). |
b) Se aplica formula pentru suma a doua cuburi si se rezolva similar exemplului precedent:
| x3 + y3 + z3 - 3xyz = (x + y)(x2 - xy + y2) + z(z2 - 3xy) = |
| = (x + y + z)(x2 - xy + y2) + z(z2 - 3xy - x2 + xy - y2) = |
| = (x + y + z)(x2 - xy + y2) + z(z2 - (x + y)2) = |
| = (x + y + z)(x2 - xy + y2 + z(z - x - y)) = |
| = (x + y + z)(x2 + y2 + z2 - xy - xz - yz). |
c) Se aplica formulele inmultirii prescurtate si se obtine
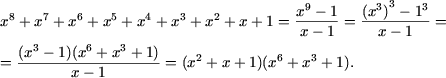
d) x5 + x + 1 = 1 + x + x2 - x2 + x5 = 1 + x + x2 - x2(1 - x3) = (1 + x + x2) - x2(1 - x)(1 + x + x2) = (1 + x + x2)(1 - x2(1 - x)) = (1 + x + x2)(1 - x2 + x3).
Exemplul 5. Sa se rationalizeze numitorii urmatoarelor expresii irationale:
Rezolvare. Se multiplica cu conjugata numitorului si se obtine:
a) ![]()
b) Similar exemplului a) se obtine
c) Se utilizeaza formula (a se vedea exemplul 4 b)):
Exemplul 6. Sa se arate ca numarul

Rezolvare. a) Se evidentiaza sub radicali patrate complete si se obtine:
b) Se evidentiaza sub semnul radacinii de ordinul trei un cub complet si se obtine
c) Se tine seama, ca

Exemplul 7. a) Sa se calculeze x2 +
y2 + z2, daca x + y + z = 1,
![]() .
.
b) Sa se arate ca egalitatea xyz = 1 implica
c) Sa se arate ca daca x + y + z = 0, atunci x4 + y4 + z4 = 2(xy + yz + zx)2.
d) Sa se demonstreze, ca pentru orice trei termeni consecutivi ai unei progresii geometrice are loc egalitatea
e) Sa se arate ca daca x1 + x2 +
x3 = y1 + y2 +
y3 = x1y1 +
x2y2 +
x3y3 = 0 si nu toate
numerele xj,
![]() si
yi,
si
yi,
![]() sunt egale cu zero,
atunci
sunt egale cu zero,
atunci
Rezolvare. a) Cum egalitatea
![]() implica xy + yz + zx = 0, rezulta
implica xy + yz + zx = 0, rezulta
b) Se observa, ca in conditia xyz = 1
Prin urmare,
c) Se tine seama ca x + y = -z si se obtine
| 2(xy + yz + zx)2 = 2(xy + z(x + y))2 = 2(xy - (x + y)2)2 = |
| = 2(x2 + xy + y2)2 = 2(x4 + x2y2 + y4 + 2x3y + 2x2y2 + 2xy3) = |
| = x4 + y4 + (y4 + 4xy3 + 6x2y2 + 4yx3 + x4) = x4 + y4 + (x + y)4 = |
| = x4 + y4 + (-z)4 = x4 + y4 + z4. |
d) Cum a1a3 = a22 (proprietatea caracteristica a progresiei geometrice) rezulta
e) Se considera vectorii (x1, x2, x3), (y1, y2, y3) si (1,1,1). Cum produsurile scalare ale acestor vectori sunt egale cu zero, rezulta ca ei sunt doi cate doi ortogonali. Asadar vectorii
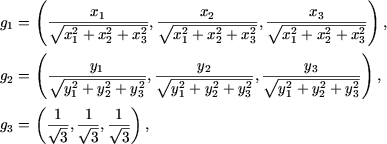
In particular, pentru x = e1 = (1,0,0), se obtine
1. Sa se determine DVA al expresiei

2. Sa se determine, daca expresiile A si B sunt identic egale pe multimea M, daca:
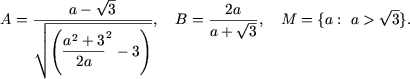
R: Da.
3. Sa se aduca la forma mai simpla expresia
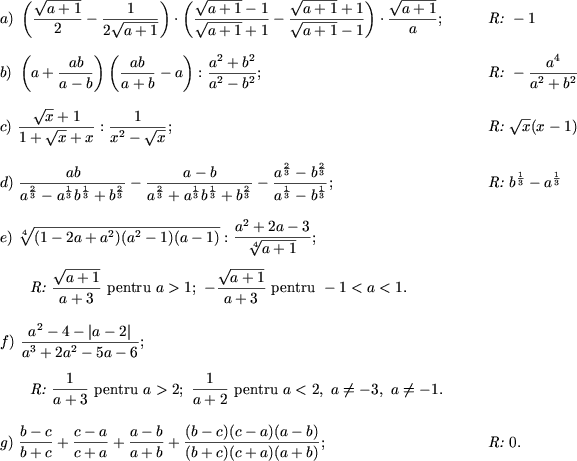
4. Sa se descompuna in factori:
| a) x4 + x2 + 1; | R: (x2 + x + 1)(x2 - x + 1) |
| b) (x - y)3 + (y - z)3 + (z - x)3; | R: 3(x - y)(y - z)(z - x). |
5. Sa se rationalizeze
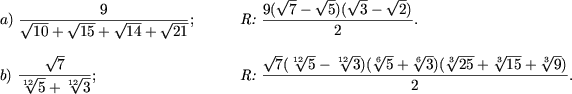
6. Sa se arate ca expresiile