| Pagina principala | Ghidul utilizatorului | Rubrica candidatului | Curriculumurile scolare |
| Matematica competitiva | Matematica distractiva| Formule, dictionare | Avizuri |
|Pagini din istorie | Examene, teste | Bibliografie | Link-uri | Site map |

Ecuatii si inecuatii de gradul al doilea si reductibile la gradul al doilea
Ecuatii de gradul al doilea

Ecuatia de forma
ax2 + bx + c = 0, (1)
unde a, b, c Î R,   a ¹ 0, x - variabila, se numeste ecuatie de gradul al doilea (ecuatia patrata).

Numerele a, b si c din (1) se numesc coeficienti ai ecuatiei de gradul al doilea, iar numarul D = b2 - 4ac se numeste discriminant al ecuatiei de gradul al doilea.

Exemplul 1. Ecuatiile ce urmeaza sunt ecuatii de gradul al doilea:

a) 6x2 + 5x + 1 = 0,   cu   a = 6,   b = 5,   c = 1   si   D = 52 - 4·6·1 = 1;
b) 9x2 - 12x + 4 = 0,   cu   a = 9,   b = -12,   c = 4   si   D = (-12)2 - 4·9·4 = 0;
c) x2 - x - 2 = 0,   cu   a = 1,   b = -1,   c = -2   si   D = (-1)2 - 4·1·(-2) = 9;
d)

Ecuatiile de gradul al doilea pot fi rezolvate conform urmatoarei afirmatii:

Afirmatia 1. Daca a) discriminantul ecuatiei (1) este pozitiv, atunci ecuatia (1) are doua radacini distincte:
(2)
b) discriminantul ecuatiei (1) este egal cu zero, atunci ecuatia (1) are doua radacini egale (o radacina de multiplicitatea doi):
(3)
c) discriminantul ecuatiei (1) este negativ, atunci ecuatia (1) nu are radacini reale.

Asadar, (a se vedea exemplul 1):

  1. ecuatia a) are doua radacini distincte x1 = -1/2 si x2 = -1/3;

  2. ecuatia b) are doua radacini egale x1 = x2 = 2/3;

  3. ecuatia c) are doua radacini distincte x1 = -1 si x2 = 2;

  4. ecuatia d) nu are radacini reale.

Ecuatia de gradul al doilea cu a = 1 se numeste ecuatie patrata redusa si se noteaza de regula
x2 + px + q = 0 (4)
si formulele (2) si (3) de calcul ale radacinilor devin
(5)

x1 = x2 = -p/2,     (D = 0). (6)

Ecuatiile de forma
ax2 + bx = 0, (7)

ax2 + c = 0. (8)
se numesc ecuatii de gradul al doilea incomplete. Ecuatiile (7), (8) pot fi rezolvate cu ajutorul afirmatiei 1 sau altfel, mai simplu:

ax2 + bx = 0   Û   x(ax + b) = 0   Û  
x1 = 0;
x2 = -b/a.
ax2 + c = 0   Û   x2 = -c/a   Û  
ac £ 0,
x Î Æ,
ac > 0.

Exemplul 2. Sa se rezolve ecuatiile

a) 2x2 - 7x = 0;       b) 9x2 - 25 = 0;       c)

Rezolvare. a)

2x2 - 7x = 0   Û   x(2x - 7) = 0   Û  
x1 = 0,
x2 = 7/2;

b) 9x2 - 25 = 0   Û   9x2 = 25   Û   x2 = 25/9   Û   x1,2 = ±5/3;

c) de unde rezulta ca ecuatia nu are radacini (membrul din stanga egalitatii este nenegativ, iar cel din dreapta - negativ).

In continuare vom analiza cateva exemple de ecuatii ce se reduc la rezolvarea ecuatiilor de gradul al doilea.

Ecuatii bipatrate.

Ecuatia de forma
ax4 + bx2 + c = 0 (9)
unde a, b, c Î R,   a ¹ 0, x - variabila, se numeste ecuatie bipatrata. Prin substitutia x2 = t (atunci x4 = t2) ecuatia bipatrata se reduce la o ecuatie de gradul al doilea.

Exemplul 3. Sa se rezolve ecuatiile

a) x4 - 29x2 + 100 = 0;       b) x4 + x2 - 6 = 0;       c) 2x4 - 3x2 + 4 = 0.

Rezolvare. a) Se noteaza x2 = t, atunci x4 = t2 si se obtine o ecuatie de gradul al doilea in t:

t2 - 29t + 100 = 0
cu solutiile t1 = 4 si t2 = 25. Astfel se obtine totalitatea de ecuatii
x2 = 4,
x2 = 25,
de unde rezulta solutiile x = ±2 si x = ±5.

b) Se procedeaza similar exemplului precedent si se obtine ecuatia patrata t2 + t - 6 = 0 cu solutiile t = -3 si t = 2. Cum t = x2 ³ 0, ramane t = 2 sau x2 = 2, de unde

c) Se utilizeaza substitutia t = x2, si se obtine ecuatia de gradul al doilea in t,   2t2 - 3t + 4 = 0 care nu are solutii reale. Prin urmare, si ecuatia enuntata nu are solutii reale.

Ecuatii simetrice de gradul patru.

Ecuatiile de forma
ax4 + bx3 + cx2 + bx + a = 0 (10)
unde a, b, c Î R,   a ¹ 0 se numesc ecuatii simetrice de gradul patru.

Prin intermediul substitutiei acest tip de ecuatii se reduce la ecuatii de gradul al doilea. In adevar, cum x = 0 nu este solutie a ecuatiei (10) (a ¹ 0), multiplicand cu ambii membri ai ecuatiei, se obtine ecuatia echivalenta

sau

Se noteaza atunci |t| ³ 2 si cum ecuatia devine

a(t2 - 2) + bt + c = 0,
adica o ecuatie de gradul al doilea, rezolvarea careia nu prezinta greutati.

Nota. Ecuatia ax4 bx3 ± cx2 ± bx + a = 0 se reduce la o ecuatie utilizand substitutia

Exemplul 4. Sa se rezolve ecuatiile

a) x4 + 5x3 + 2x2 + 5x + 1 = 0,
b) 2x4 + 3x3 - 4x2 - 3x + 2 = 0.

Rezolvare. a) Ecuatia data este o ecuatie simetrica de gradul patru. Cum x = 0 nu e solutie, ecuatia este echivalenta cu ecuatia (se divide la x2 ¹ 0 si se grupeaza convenabil)

Se noteaza ,   |t| ³ 2, atunci si ecuatia devine
t2 - 2 + 5t + 2 = 0
sau t2 + 5t = 0, cu solutiile t1 = -5, t2 = 0 (nu se verifica conditia |t| ³ 2). Prin urmare,
de unde rezulta ecuatia patrata x2 + 5x + 1 = 0 cu solutiile si

b) Cum x = 0 nu este solutie a ecuatiei date, se divide cu x2 si se obtine ecuatia

Se noteaza atunci si se obtine ecuatia patrata
2(t2 + 2) + 3t - 4 = 0   sau   2t2 + 3t = 0,
cu solutiile t1 = 0 si t2 = -3/2. Prin urmare
Din prima ecuatie a sistemului se obtine x = -1 si x2 = 1, iar din a doua x3 = -2 si x4 = 1/2.

Ecuatii reversibile

Ecuatia
ax4 + bx3 + cx2 + dx + e = 0, (11)
unde {a, b, c, d} Ì R,   a ¹ 0,   b ¹ 0 si se numeste ecuatie reversibila de gradul patru.

Acest tip de ecuatii se reduc la ecuatii de gradul al doilea utilizand substitutia

Exemplul 5. Sa se rezolve ecuatia

x4 + x3 - 6x2 - 2x + 4 = 0.

Rezolvare. Se observa ca si prin urmare ecuatia este o ecuatie reversibila de gradul patru. Cum x = 0 nu este soltuie, se divide la x2 (si nu se pierd solutii), si se obtine ecuatia

Se noteaza atunci de unde si se obtine ecuatia de gradul al doilea

t2 + 4 + t - 6 = 0   sau   t2 + t - 2 = 0
cu solutiile t1 = -2 si t2 = 1. Astfel se obtine totalitatea
sau, echivalent (x ¹ 0)
x2 + 2x - 2 = 0,
x2 - x - 2 = 0,
de unde se obtin solutiile x = -1 si x = 2.

Ecuatii de forma

(x + a)4 + (x + b)4 = c. (12)

Se utilizeaza substitutia si se reduce la o ecuatie bipatrata in raport cu t.

Exemplul 6. Sa se rezolve ecuatia

(x + 3)4 + (x - 1)4 = 82.

Rezolvare. Se utileaza substitutia si se obtine ecuatia echivalenta in t:

(t + 2)4 + (t - 2)4 = 82
sau
t4 + 8t3 + 24t2 + 32t + 16 + t4 - 8t3 + 24t2 - 32t + 16 - 82 = 0
de unde rezulta ecuatia bipatrata
t4 + 24t2 - 25 = 0
cu solutia t2 = 1, de unde t = ± 1 si x + 1 = ± 1 conduce la solutiile x = -2 si x = 0.

Ecuatia de forma
(x + a)(x + b)(x + c)(x + d) = m (13)
unde a + b = c + d.

Acest tip de ecuatii se reduce la ecuatii de gradul doi utilizand esential conditia a + b = c + d. In adevar,

(x + a)(x + b) = x2 + (a + b)x + ab
(x + c)(x + d) = x2 + (c + d)x + cd = x2 + (a + b)x + cd
si notand x2 + (a + b)x = t (sau x2 + (a + b)x + ab = t) se obtine ecuatia patrata (t + ab)(t + cd) = m (respectiv t(t + cd - ab) = m).

Exemplul 7. Sa se rezolve ecuatia

(x - 2)(x + 1)(x + 4)(x + 7) = 19.

Rezolvare. Se observa ca -2 + 7 = 1 + 4, se grupeaza convenabil

[(x - 2)(x + 7)]·[(x + 1)(x + 4)] = 19
si se deschid parantezele rotunde
[x2 + 5x - 14][x2 + 5x + 4] = 19.
Se noteaza t = x2 + 5x - 14, atunci x2 + 5x + 4 = t + 18 si ecuatia devine
t(t + 18) = 19   sau   t2 + 18t - 19 = 0
cu solutiile t = -19 si t = 1. Asadar, se obtine totalitatea de ecuatii
x2 + 5x - 14 = -19,
x2 + 5x - 14 = 1,
cu solutiile si

Ecuatii fractionar-rationale

Exemplul 8. Sa se rezolve ecuatiile:

Rezolvare. a) DVA al ecuatiei este In DVA ecuatia este echivalenta cu ecuatia (se multiplica ambii membri ai ecuatiei cu (5x - 4)(x + 3)):

(3x + 4)(x + 3) - (2x - 1)(5x - 4) = 0
de unde, deschizand parantezele, se obtine ecuatia patrata
7x2 - 26x - 8 = 0
cu solutiile x1 = -2/7 si x2 = 4. Ambele solutii verifica DVA.

b) DVA al ecuatiei este R\{2;3}. Se multiplica ambii membri ai ecuatiei cu (x - 2)(x - 3) (in DVA acest produs este diferit de zero) si se obtine ecuatia

x - 1 + (x - 2)(x - 3) + x - 3 = 0
sau
x2 - 3x + 2 = 0
cu solutiile x1 = 1 si x2 = 2. Cum ultima radacina nu verifica DVA ramane x = 1.

c) DVA al ecuatiei este R\{3;4;5;6}. Se grupeaza convenabil

si se aduce la numitor comun in fiecare paranteza

Se multiplica cu (x - 6)(x - 3)(x - 4)(x - 5) ( ¹ 0 pe DVA) si se obtine ecuatia

(2x - 9)(x - 4)(x - 5) + (2x - 9)(x - 6)(x - 3) = 0
sau
(2x - 9)[(x - 4)(x - 5) + (x - 6)(x - 3)] = 0,
de unde rezulta totalitatea de ecuatii
2x - 9 = 0,
x2 - 9x + 19 = 0
cu solutiile

d) DVA al ecuatiei este R\{1;3;4;5}. Se evidentiaza partea intreaga a fiecarui termen al ecuatiei:

sau
de unde
sau

Se aduce in fiecare membru la numitor comun si se obtine

sau
2x(x - 4)(x - 5) - x(x - 1)(x - 3) = 0,
de unde rezulta totalitatea de ecuatii
x = 0,
x2 - 14x + 37 = 0,
cu solutiile x1 = 0 si (toate solutiile sunt din DVA).

Ecuatii de forma

(14)

Acest tip de ecuatii se reduc la ecuatii patrate utilizand substitutia

Exemplul 9. Sa se rezolve ecuatia

Rezolvare. DVA al ecuatiei este Cum x = 0 nu este solutie a acestei ecuatii, ecuatia se scrie

(numaratorul si numitorul fractiilor din membrul stang al ecuatiei se divid cu x).

Se noteaza si ecuatia devine

sau 2(t + 1) + 13(t - 5) = 6(t - 5)(t + 1), de unde rezulta ecuatia patrata
6t2 - 39t + 33 = 0   sau   2t2 - 13t + 11 = 0
cu solutiile t1 = 1 si t2 = 11/2 (ambele solutii verifica restrictiile t ¹ 5 si t ¹ -1). Prin urmare, se obtine totalitatea de ecuatii
  sau  
2x2 - x + 3 = 0,
4x2 - 11x + 6 = 0
cu solutiile x1 = 3/4 si x2 = 2.

Ecuatii ce contin expresii reciproc inverse

Ecuatiile de forma
(15)
se reduc la ecuatii patrate prin substitutia atunci si ecuatia (15) se scrie at2 + ct + b = 0.

Exemplul 10. Sa se rezolve ecuatiile

Rezolvare. a) DVA al ecuatiei este Se noteaza atunci si ecuatia devine

de unde rezulta ecuatia t2 - 5t + 4 = 0 cu solutiile t1 = 1 si t2 = 4. Astfel se obtine totalitatea de ecuatii de gradul intai
cu solutiile x = -1 si x = 1/2 (ambele solutii verifica DVA).

b) DVA al ecuatiei este R\{± 1}. Se observa, ca x = ± 2 nu verifica ecuatia data si prin urmare multiplicand ecuatia cu se obtine ecuatia echivalenta

Se noteaza si ecuatia devine
  sau   20t2 + 48t - 5 = 0
cu solutiile t1 = 1/10 si t2 = -5/2. Astfel se obtine totalitatea de ecuatii
  sau  
3x2 - 11x + 6 = 0,
7x2 + 9x + 14 = 0,
cu solutiile x1 = 3,   x2 = 2/3 (ambele solutii sunt din DVA).

In unele cazuri este comod de separat un patrat complet.

Exemplul 11. Sa se rezolve ecuatiile

a) x4 - 2x3 - x2 + 2x + 1 = 0;
b)

Rezolvare. a) Se separa un patrat complet

x4 - 2x2·x + x2 - x2 - x2 + 2x + 1 = 0,
(x2 - x)2 - 2(x2 - x) + 1 = 0.
Se noteaza t = x2 - x si se obtine ecuatia patrata
t2 - 2t + 1 = 0
de unde t = 1, sau x2 - x - 1 = 0, cu solutiile

b) DVA al ecuatiei este Se aduna in ambii membri ai ecuatiei expresia

si se obtine
sau
de unde rezulta ecuatia
Se noteaza si ecuatia devine
t2 - t - 2 = 0.
Solutiile acestei ecuatii sunt t = -1 si t = 2, prin urmare se obtine totalitatea de ecuatii
  sau  
2x2 + 2x - 1 = 0,
x2 - 2x + 1 = 0,
cu solutiile si x3 = 1.

Inecuatii de gradul doi si inecuatii reductibile la cele se gradul doi

Prin inecuatie de gradul al doilea se intelege una din urmatoarele inecuatii
ax2 + bx + c > 0, (16)
ax2 + bx + c ³ 0, (17)
ax2 + bx + c < 0, (18)
ax2 + bx + c £ 0, (19)
unde a, b, c Î R,   a ¹ 0.

Inecuatiile de gradul al doilea se rezolva utilizand urmatoarele afirmatii.

Afirmatia 2. Daca a > 0 si discriminantul trinomului ax2 + bx + x este pozitiv, atunci:

  1. inecuatia (16) are solutiile x Î (-¥;x1)È(x2;+¥);
  2. inecuatia (17) are solutiile x Î (¥;x1]È[x2;+¥);
  3. inecuatia (18) are solutiile x Î (x1,x2);
  4. inecuatia (19) are solutiile x Î [x1,x2]

unde x1 si x2 (x1 < x2) sunt radacinile trinomului ax2 + bx + c.

Afirmatia 3. Daca a > 0 si discriminantul trinomului ax2 + bx + c este egal cu zero, atunci

  1. inecuatia (16) are solutiile x Î R\{x1};
  2. inecuatia (17) are solutiile x Î R;
  3. inecuatia (18) nu are solutii;
  4. inecuatia (18) are o solutie unica: x = x1,

unde x1 este radacina dubla a trinomului ax2 + bx + c.

Afirmatia 4. Daca a > 0 si dscriminantul trinomului ax2 + bx + c este negativ, atunci

  1. inecuatiile (16) si (17) au solutiile x Î R;
  2. inecuatiile (18) si (19) nu au solutii.

Daca a < 0 inecuatile (16)-(19) se multiplica prin (-1) si schimband semnul inecuatiei in opusul lui se obtine o inecuatie cu a > 0 si se aplica afirmatiile 2-4.

Exemplul 12. Sa se rezolve inecuatiile

a) x2 - x - 90 > 0; d) x2 - x + 2 > 0;
b) 4x2 - 12x + 9 £ 0;         e) -6x2 + 5x - 1 £ 0;
c) x2 - 6x < 0; f) 4x2 - x + 5 £ 0.

Rezolvare. a) Cum radacinile trinomului x2 - x - 90 sunt x1 = -9 si x2 = 10, a = 1 > 0, solutiile inecuatiei x2 - x - 90 > 0 sunt x Î (-¥;-9)È(10;+¥).

b) Cum discriminatul trinomului 4x2 - 12x + 9 este egal cu zero, a = 4 > 0, unica solutie a inecuatiei 4x2 - 12x + 9 £ 0 este x = 3/2.

c) Radacinile trinomului x2 - 6x sunt x1 = 0 si x2 = 6. Cum a = 1 > 0, solutiile inecuatiei x2 - 6x < 0 sunt x Î (0;6).

d) Discriminantul trinomului x2 - x + 2 este negativ, a = 1 > 0, prin urmare, orice numar real este solutie a inecuatiei x2 - x + 2 > 0.

e) Se multiplica ambii membri ai inecuatiei cu -1 si se obtine inecuatia 6x2 - 5x + 1 ³ 0 cu solutiile x Î (-¥;1/3]È[1/2;+¥).

f) Inecuatia data nu are solutii.

Metodele de reducere ale ecuatiilor de grad superior la ecuatii de gradul al doilea raman valabile si in cazul inecuatiilor. In unele cazuri se utilizeaza in plus metoda intervalelor (a se vedea [1]-[4]).

Exemplul 13. Sa se rezolve inecuatiile

a) 6x4 + 5x3 - 38x2 + 5x + 6 £ 0;
b) x(x - 2)(x - 4)(x - 6) ³ 9;
c) x4 - 4x3 + 8x + 3 < 0;
d)
e) 50x4 - 105x3 + 74x2 - 21x + 2 ³ 0;
f)
g) (x + 5)4 + (x + 3)4 < 272.

Rezolvare. a) Se rezolva ecuatia (a se vedea (10 ))

6x4 + 5x3 - 38x2 + 5x + 6 = 0
si se determina zerourile membrului din stanga inecuatiei:

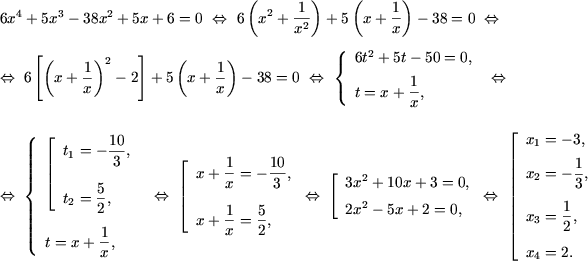
Prin urmare

de unde, utilizand metoda intervalelor, se obtine multime solutiilor inecuatiei initiale x Î [-3;-1/3]È[1/2;2].

b) Se tine seama de metoda de rezolvare a ecuatiilor de tip (13) si se obtine

x(x - 2)(x - 4)(x - 6) ³ 9   Û   x(x - 6)(x - 2)(x - 4) - 9 ³ 0   Û
Û   (x2 - 6x)(x2 - 6x + 8) - 9 ³ 0   Û  
t(t + 8) - 9 ³ 0,
t = x2 - 6x,
   Û
Û  
t2 + 8t - 9 ³ 0,
t = x2 - 6x,
   Û  
t £ -9,
t ³ 1
t = x2 - 6x,
   Û  
x2 - 6x £ -9,
x2 - 6x ³ 1,
   Û
Û  
x2 - 6x + 9 £ 0,
x2 - 6x - 1 ³ 0,
   Û  
x = 3,
   Û

c) Se separa un patrat complet,

x4 - 4x3 + 8x + 3 < 0   Û   (x2)2 - 2·2·x2·x + 4x2 - 4x2 + 8x + 3 < 0   Û
Û   (x2 - 2x) - 4(x2 - 2x) + 3 < 0   Û  
t2 - 4t + 3 < 0,
t = x2 - 2x,
   Û  
1 < t < 3,
t = x2 - 2x,
   Û
Û  
x2 - 2x < 3,
x2 - 2x > 1,
   Û  
x2 - 2x - 3 < 0,
x2 - 2x - 1 > 0,
   Û  
-1 < x < 3,
   Û  

d) Se utilizeaza metoda intervalelor

Û   x Î (0;1)È(3;5).

e) Se rezolva ecuatia (a se vedea (11))

50x4 - 105x3 + 24x2 - 21x + 2 = 0
si se determina zerourile membrului din stanga inecuatiei (se tine seama ca x = 0 este solutie a inecuatiei).

Prin urmare

Se utilizeaza metoda intervalelor si se obtine x Î (-¥;1/5]È[2/5;1/2]È[1;+¥).

f) Cum x = 0 nu este solutie a inecuatiei (0 > 1) inecuatia enuntata este echivalenta cu inecuatia

Se noteaza atunci si inecuatia devine

Se rezolva cu ajutorul metodei intervalelor si se obtine

Prin urmare

  de unde     sau
x > 0,
x < 0,
x > 0,
x < 0,
1 < x < 7,
   Û  
x Î Æ,
x Î (1;7),
   Û   x Î (1;7).

g) Se grupeaza t = x + 4 (a se vedea (12)) si inecuatia devine

(t + 1)4 + (t - 1)4 < 272
sau
t4 + 6t2 - 135 < 0
de unde rezulta
(t2 - 9)(t2 + 15) < 0   sau   |t| < 3.

Prin urmare |x + 4| < 3. Se utilizeaza proprietatile modulului si se obtine

|x + 4| < 3   Û   -3 < x + 4 < 3   Û   -7 < x < -1.

Exercitii pentru autoevaluare

I. Sa se rezolve ecuatiile

  1. x(x + 1)(x + 2)(x + 3) = 24.

  2. (1 - x)(2 - x)(x + 3)(x + 3) = 84.

  3. (x + 2)4 + x4 = 82.

  4. (2x2 + 5x - 4)2 - 5x2(2x2 + 5x - 4) + 6x4 = 0.

  9. x4 - 4x3 + 2x2 + 4x + 2 = 0.

  10. x4 + 6x3 + 5x2 - 12x + 3 = 0.

  13. (x2 + x + 1)(x2 + x + 2) = 12.

  15. 6x4 - 5x2 + 1 = 0.

II. Sa se rezolve inecuatiile

  2. x4 - 8x3 + 14x2 + 8x - 15 £ 0.

  6. x4 + x3 - 12x2 - 26x - 24 < 0.

  8. (x - 1)(x - 2)(x + 3)(x + 4) ³ 84.

  9. (x - 1)4 + (x + 1)4 ³ 82.

Bibliografie


| Pagina principala | Ghidul utilizatorului | Rubrica candidatului | Curriculumurile scolare |
| Matematica competitiva | Matematica distractiva| Formule, dictionare | Avizuri |
|Pagini din istorie | Examene, teste | Bibliografie | Link-uri | Site map |