Progresii

Progresii aritmetice si geometrice

Progresia aritmetica.

Definitia 1. Sirul numeric (a_n)_{n
Î N} se numeste progresie aritmetica, daca exista un numar real d, numit ratia progresia, astfel incat
a_n+1 - a_n = d, ("n Î N) (1)

adica daca fiecare termen al sirului (incepand cu al doilea) este egal cu precedentul plus unul si acelasi numar (ratia).

Elementul a_n se numeste termen general al progresiei sau termen de rang n.

Exemplul 1. Sa se verifice daca sirurile ce urmeaza formeaza o progresie aritmetica

a) a_n = 2n - 1, b) 3, 6, 9, ..., 3k, ... c) a_n = ¹/_n.

Rezolvare. a) Cum diferenta a_n+1 - a_n reprezinta un numar constant

a_n+1 - a_n = 2(n + 1) - 1 - (2n - 1) = 2 pentru orice n Î N, rezulta ca sirul dat de termenul general a_n = 2n - 1 reprezinta o progresie aritmetica cu ratia 2, si anume 1, 3, 5, ..., 2n - 1, ...

b) Similar exemplului a) se obtine

a_n+1 - a_n = 3(n + 1) - 3n = 3, ("n Î N) si prin urmare sirul dat formeaza o progresie aritmetica cu ratia 3.

c) Se scriu primii trei termeni ai sirului a₁ = 1, a₂ = ¹/₂, a₃ = ¹/₃ si se observa ca a₂ - a₁ = -¹/₂ š a₃ - a₂ = -¹/₆, adica sirul dat nu formeaza o progresie aritmetica.

Altfel, se considera diferenta si se observa ca ea depinde de n (nu este un numar constant) si prin urmare sirul dat nu este o progresie aritmetica.

Proprietati ale progresiei aritmetice

Demonstratiile proprietatilor ce urmeaza, pot fi gasite, de exemplu, in [1].

P1. Termenul general al progresiei aritmetice se poate determina prin formula

a_n = a₁ + (n - 1)d, (2)

unde a₁ - primul termen al progresiei, d - ratia ei.

P2. (Proprietatea caracteristica a progresiei aritmetice). Termenul de rang n este media aritmetica a termenilor echidistanti de el:

a_n-k + a_n+k = 2·a_n, (3)

Nota. Din propretatea P2 rezulta ca conditia necesara si suficienta ca

a) trei numere a, b, c (in ordinea data) sa formeze o progresie aritmetica este

2b = a + b, (4)

b) trei numere a, b, c (fara precizarea consecutivitatii) sa formeze o progresie aritmetica este

(2b - a - c)(2c - a - b)(2a - b - c) = 0. (5)

P3. Daca a₁, a₂, ..., a_n, ... este o progresie aritmetica si k + n = m + p (k,n,m,p Î N), atunci

a_k + a_n = a_m + a_p. (6)

P4. Formula sumei S_n primilor n termeni ai progresiei aritmetice:

(7)

sau tinand seama de (2)

(8)

Definitia 2. Progresia aritmetica este un sir crescator (descrescator), daca si numai daca ratia ei este un numar pozitiv (negativ). Daca ratia progresiei este zero avem un sir constant.

In continuare sa anlizam cateva exemple.

Exemplul 2. Sa se determine progresia aritmetica, daca a₃ = 2 si a₅ = -2.

Rezolvare. Se aplica formula teremenul general al progresiei aritmetice si se obtine sistemul

	a₃ = a₁ + 2d,
	a₅ = a₁ + 4d,

sau, tinand seama de conditiile problemei obtinem

	a₁ + 2d = 2,
	a₁ + 4d = -2,

de unde se obtine primul termen al progresiei a₁ = 6 si ratia progresiei d = -2.

Exemplul 3. Sa se determine numarul x, astfel ca numerele a - x, x, b (a, b fiind date), luate in aceasta ordine sa formeze o progresie aritmetica.

Rezolvare. Se utilizeaza proprietatea caracteristica a progresiei aritmetice si se obtine ecuatia liniara

2x = a - x + b, cu solutia

Exemplul 4. Sa se determine progresia aritmetica, suma primilor n termeni ai careia se exprima prin formula

S_n = 3n² + 6n (n ł 1).

Rezolvare. Cum suma primilor (n - 1) termeni este

S_n-1 = 3(n - 1)² + 6(n - 1) = 3n² - 3, (n ł 2) si cum S_n - S_n-1 = a_n, rezulta a_n = 3n² + 6n - 3n² + 3 = 6n + 3.

Substituind in formula termenului general, consecutiv n = 1, 2, 3, ... se obtine a₁ = 9, a₂ = 15, a₃ = 21, ...

Exemplul 5. Sa se determine suma primilor nouasprezece termeni ai progresiei aritmetice a₁, a₂, a₃, ..., daca

a₄ + a₈ + a₁₂ + a₁₆ = 224.

Rezolvare. Se observa ca 4 + 16 = 8 + 12 si, prin urmare, (a se vedea (6)) a₄ + a₁₆ = a₈ + a₁₂. Se tine seama ca suma acestor termeni este 224, si se obtine a₄ + a₁₆ = 112.

Cum (a se vedea (7)) si a₁ + a₁₉ = a₄ + a₁₆ = 112 (1 + 19=4 + 16), rezulta

Exemplul 6. Pentru ce valori ale parametrului a exista asa valori ale variabilei x astfel incat numerele

5^1+x + 5^1-x, ^a/₂, 25^x + 25^-x sunt termeni consecutivi ai unei progresii aritmetice.

Rezolvare. Conform proprietatii caracteristice a progresiei aritmetice, se obtine ecuatia

a = 5^1+x + 5^1-x + 25^x + 25^-x.

Se observa ca pentru a Ł 0 ecuatia nu are solutii (membrul din dreapta, ca suma de termeni pozitivi, este un numar pozitiv).

Cum a^{x + y} = a^x·a^y, (a > 0, a š 1), ecuatia se scrie

Se noteaza , t ł 2 (suma a doua marimi pozitive inverse), atunci

si ecuatia devine t² + 5t - (a + 2) = 0.

Cel putin o radacina a acestei ecuatii urmeaza a fi mai mare ca doi (ecuatia data are doua radacini reale distincte, deoarece pentru a > 0, -(a+2) < 0 si coeficientul de pe langa t², 1 > 0), pentru ce este suficient ca sa se verifice sistemul

	-^b/_2a < 2,
	f(2) Ł 0,

	-⁵/₂ < 2,
	4 + 10 - (a + 2) Ł 0,

de unde a ł 12.

Exemplul 7. Sa se determine suma tuturor numerelor pare de trei cifre, divizibile la 3.

Rezolvare. Primul numar par de trei cifre, divizibil la 3 este 102. Cum numarul par, divizibil la 3 se divide si la 6, se obtine progresia

102, 108, 114, ..., 996, cu a₁ = 102, d = 6 si ultimul termen a_x = 996 (x Î N).

Se tine seama ca a_x = a₁ + (x - 1)d sau

102 + (x - 1)·6 = 996, de unde, numarul tuturor numerelor pare de trei cifre divizibile prin trei, x = 150. Astfel, utilizand formula (7) se obtine

Exemplul 8. Fie S_n, S_m si S_p suma primilor n, respectiv m si p, termeni ai progresiei aritmetice a₁, a₂, a₃, .... Sa se arate ca

(9)

Rezolvare. Se tine seama de formula (8) si egalitatea (9) devine

sau 2a₁[m - p + p - n + n - m] + [(n - 1)(m - p) + (m - 1)(p - n) + (p - 1)(n - m)]d = 0.

Cum

(n - 1)(m - p) + (m - 1)(p - n) + (p - 1)(n - m) =

= nm - np - m + p + mp - mn - p + n + pn - pm - n + m = 0

se obtine 2a₁·0 + 0·d = 0, adica 0 = 0, si prin urmare, egalitatea este demonstrata.

Exemplul 9. Sa se determine numerele, ce sunt termeni comuni ai progresiilor aritmetice 2, 5, 8, ..., 332 si 7, 12, 17, ..., 157.

Rezolvare. Fie b este termenul de rang n in prima progresie si, prin urmare, b = 2 + (n - 1)·3 si in acelasi timp, este termenul de rang m in a doua progresie, adica b = 7 + (m - 1)·5. Asadar se obtine ecuatia

2 + (n - 1)·3 = 7 + (m - 1)·5, sau 3(n - 1) = 5m de unde, tinand seama ca m, n sunt numere naturale, se obtine n = 5k + 1 si m = 3k, k Î N, adica termenii a₆, a₁₁, a₁₆, ..., a_5k+1 din prima progresie coincid cu termenii c₃, c₆, c₉, ..., c_3k, din a doua progresie. Asadar, termenii comuni sunt: 17, 32, 47, 62, 77, 92, 107, 122, 137 si 152.

Exemplul 10. Suma a trei numere pozitive a, b si g este egala cu ^p/₂. Sa se determine produsul ctga· ctgg daca ctga, ctgb, ctgg formeaza o progresie aritmetica.

Rezolvare. Se tine seama de proprietatea caracteristica a progresiei aritmetice si se obtine relatia

2ctgb = ctga + ctgg. Cum a + b + g = ^p/₂ implica b = ^p/₂ - (a + g), se utilizeaza formula de reducere ctg(^p/₂ - x) = tgx si se obtine 2tg(a + b) = ctga + ctgb sau, folosind formulea tangentei sumei a doua unghiuri

de unde,

sau, tinand seama ca a, b si g sunt numere pozitive si sumalor este ^p/₂ (tgatgg š 1, tga š 0, tgg š 0) se obtine 2tgatgg = 1 - tgatgg de unde rezulta tgatgg = ¹/₃ si, prin urmare, ctgactgg = 3.

Exemplul 11. Fie ecuatia patrata x² + px + q = 0 cu radacinile reale x₁ si x₂. Sa se determine p si q astfel incat q, x₁, p, x₂ (in ordinea indicata) sa formeze o progresie aritmetica crescatoare.

Rezolvare. Se utilizeaza proprietatea caracteristica a progresiei aritmetice, teorema lui Viete si se obtine sistemul

	2x₁ = q + p,
	2p = x₁ + x₂,
	x₁ + x₂ = -p,
	x₁x₂ = q,

cu solutiile

	q = -4,
	x₁ = -2,
	p = 0,
	x₂ = 2,

	q = 0,
	x₁ = 0,
	p = 0,
	x₂ = 0

Cum progresia urmeaza a fi crescatoare, ramane q = -4, x₁ = -2, p = 0, x₂ = 2 si prin urmare ecuatia patrata ce verifica conditiile problemei date este x² - 4 = 0 cu p = 0 si q = -4.

Exemplul 12. Sa se determine primii trei termeni ai unei progresii aritmetice, descrescatoare, daca a₁ + a₃ + a₅ = -24 si a₁a₃a₅ = 640.

Rezolvare. Se utilizeaza proprietatea P3 si se determina a₃ = -8, dupa ce se obtine sistemul

	a₁ + a₅ = -16,
	a₁a₅ = -80,

cu solutiile a˘₁ = -20, a˘₅ = 4 si a˘˘₁ = 4, a˘˘₅ = -20. Cum progresia este descrescatoare (d < 0) ramane a₁ = 4 si a₅ = -20. Se utilizeaza P3 si se obtine

Asadar primii trei termeni ai progresiei sunt 4, -2 si -8.

Progresia geometrica

Definitia 2. Sirul numeric (b_n)_{n
Î N} se numeste progresie geometrica, daca exista asa un numar q, numit ratia progresiei, astfel incat

b_n+1 = b_n·q, ("n Î N) adica daca fiecare termen al sirului (incepand cu al doilea) este egal cu produsul dintre termenul precedent si unul si acelasi numar (ratia).

Elementul b_n se numeste termen general al progresiei de rang n.

Urmatoarele siruri reprezinta progresii geometrice:

2, 4, 8, ..., 2ⁿ, ...	cu b₁ = 2 si q = 2,
3, -1, ¹/₃, -¹/₃,...	cu b₁ = 3 si q = -¹/₃,
a, a, a, ...	cu b₁ = a si q = 1,
a, 0, 0, ...	cu b₁ = a si q = 0

Tinem sa mentionam, ca daca unul din termenii progresiei geometrice este egal cu zero, atunci sau b₁ = 0 sau q = 0.

Proprietatile progresiei geometrice

P5. Termenul de rang n al progresiei geometrice se determine prin formula

b_n = b₁·q^n-1, ("n Î N). (11)

P6. (Proprietatea caracteristica a unei progresii geometrice). Patratul termenului de rang n este egal cu produsul termenilor echidistanti de el:

(12)

in caz particular, pentru orice trei termeni consecutivi

(13)

Nota. Formulele (12), (13) se pot scrie si astfel

(14)

(15)

adica modulul termenului de rang n este media geometrica a termenilor echidistanti de el. In cazul progresiei cu termeni pozitivi insasi termenul de rang n este media geometrica a termenilor echidistanti de el

(16)

P7. Daca k + n = m + p (k, n, m, p Î N), atunci

b_k·b_n = b_m·b_p, (17)

unde b_k, b_n, b_m, b_p - termeni ai progresiei geometrice b₁, b₂, ....

P8. Trei numere a, b, c formeaza o progresie geometrica (fara a preciza consecutivitatea lor) daca si numai daca verifica relatia:

(a² - bc)(b² - ac)(c² - ab) = 0, (18)

iar numerele a, b, c formeaza o progresie geometrica (in ordinea indicata) daca si numai daca

b² = ac.

P9. Suma primilor n termeni S_n ai unei progresii geometrice se determina prin formula

(19)

unde b₁ - primul termen, q - ratia, si b_n - termenul general al progresiei geometrice.

In caz q = 1 suma primilor n termeni se determina prin formula

S_n = b₁·n. (20)

P10. Suma S a tuturor termenilor ai progresiei geometrice infinit descrescatoare (|q| < 1) se determina prin formula

(21)

In continuare sa analizam cateva exemple.

Exemplul 13. Produsul primilor trei termeni ai unei progresii geometrice este egal cu 1728, iar suma lor este egala cu 63. Sa se determine primul termen si ratia progresiei.

Rezolvare. Fie primii termeni ai progresiei b₁, b₂ si b₃. Atunci din conditia b₁b₂b₃ = 1728 rezulta (a se vedea (12)) si b₂ = 12. Astfel se obtine sistemul:

	b₁b₃ = 144,
	b₁ + b₃ = 51,

solutiile caruia sunt si solutiile (a se vedea teorema reciproca a lui Viete) ecuatiei patrate z² - 51z + 144 = 0. Se rezolva ecuatia si se obtine z₁ = 3 si z₂ = 48, adica b₁ = 3, b₃ = 48 sau b₁ = 48, b₃ = 3. Cum b₁ = 3, b₂ = 12 sau b₁ = 48 si b₂ = 12 se obtine q = 4 sau q = ¹/₄. Asadar solutiile problemei sunt b₁ = 3 si q = 4 sau b₁ = 48 si q = ¹/₄.

Exemplul 14. Intr-o progresie geometrica cu termeni pozitivi termenul de rangul (m + n) este egal cu p, iar termenul de rangul (m - n) (m > n) este s. Sa se determine termenul de rang m si termenul de rang n.

Rezolvare. Cum (a se vedea (11))

rezulta

si cum b_m > 0, se obtine

Conform conditiilor problemei si formulei (10 ) avem

	b₁q^m+n-1 = p,
	b₁q^m-n-1 = s,

de unde

si prin urmare

Cum b₁q^m+n-1 = b₁q^n-1·q^m = b_n·q^m = p, rezulta

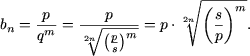
Exemplul 15. Sa se calculeze suma

Rezolvare. Avem

sau ⁹/₇·S_n = (10 - 1) + (100 - 1) + (10³ - 1) + ... + (10ⁿ - 1) de unde ⁹/₇·S_n = (10 + 10² + 10³ + ... + 10ⁿ) - n. Cum in paranteze se afla suma primilor n termeni ai progresiei geometrice cu primul termen b₁ = 10 si ratia q = 10 se utilizeaza formula (19) si se obtine

de unde

Exemplul 16. Sa se arate ca numerele 9, 10, 11 nu pot fi termeni ai unei progresii geometrice.

Rezolvare. Fie ca numerele date sunt termeni ai progresiei geometrice cu primul termen b₁ si ratia q. Atunci 9 = b₁q^k-1, 10 = b₁q^n-1 si 11 = b₁q^m-1, de unde rezulta

Asadar

de unde

Cum m, n, k sunt numere naturale diferite, aceasta egalitate nu are loc si, prin urmare, numerele 9, 10, si 11 nu pot fi termeni ai unei progresii geometrice.

Exemplul 17. Numerele a, b, c, d formeaza o progresie geometrica. Sa se arate ca (a - c)² + (b - c)² + (b - d)² = (a - d)².

Rezolvare. Se dezvolta membrul din stanga egalitatii

A = a² - 2ac + c² + b² - 2bc + c² + b² - 2bd + d². Se tine seama ca b² = ac, c² = bd si bc = ad (a se vedea (12) si (17)), si se obtine A = a² - 2b² + c² + b² - 2bc + c² + b² - 2c² + d² = a² - 2bc + d² = a² - 2ad + d² = (a - d)².

Exemplul 18. Suma termenilor unei progresii geometrice infinit descrescatoare este egal cu 4, iar suma cuburilor termenilor ei este egala cu 192. Sa se determine termenul de rang 5.

Rezolvare. Fie b₁ si q - primul termen si ratia progresiei geometrice date. Atunci |q| < 1 si

Se observa ca cuburile termenilor progresiei initiale la fel formeaza o progresie geometrica infinit descrescatoare cu primul termen

si ratia q³. In adevar, cum

rezulta

Astfel se obtine sistemul

Se determina b₁ din prima ecuatie: b₁ = 4(1 - q) si se substituie in a doua:

de unde (|q| < 1) rezulta ecuatia (1 - q)² = 3(1 + q + q²) sau 2q² + 5q + 2 = 0 cu solutiile q₁ = -2 si q₂ = -¹/₂. Cum |q| < 1 ramane q = -¹/₂ si prin urmare b₁ = 6. Se utilizeaza formula termenului de rang n si se obtine

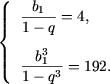
Exemplul 19. Sa se rezolve ecuatia:

Rezolvare. Se observa ca in numaratorul membrului din stanga se afla suma termenilor unei progresii geometrice infinit descrescatoare cu primul termen b₁ = 1 si ratia q₁ = tgx, iar in numitorul membrului din stanga - suma termenilor unei progresii geometrice infinit descrescatoare cu primul termen 1 si ratia (-tgx). Cum |tgx| < 1 ecuatia se scrie

Cum

iar

ecuatia devine

de unde rezulta totalitatea

Cum |tgx| < 1, ramane x = pn, n Î Z.

Probleme combinate

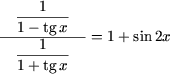
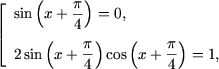
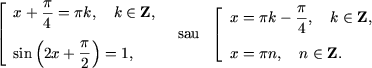
Exemplul 20. Sa se determine numerele a, b si c daca se stie ca a, b, c sunt trei termeni consecutivi ai unei progresii geometrice; a, b + 2, c formeaza o progresie aritmetica, iar a, b + 2, c + 9 formeaza o progresie geometrica.

Rezolvare. Se utilizeaza proprietatile caracteristice ale progresiilor geometrice si aritmetice si se obtine sistemul

	b² = ac,
	2(b + 2) = a + c,
	(b + c)² = a(c + 9),

cu solutiile a = 4, b = 8, c = 16 sau

Exemplul 21. Sa se arate, ca daca numerele pozitive a, b, c sunt respectiv termenii de rang m, n, p atat a unei progresii aritmetice cat si geometrice, atunci a^b-c·b^c-a·c^a-b = 1.

Rezolvare. Conform conditiilor

a = a₁ + (m - 1)d,

b = a₁ + (n - 1)d,

c = a₁ + (p - 1)d,

(22)

unde a₁ si d desemneaza primul termen si ratia progresiei aritmetice.

Din egalitatile (22) rezulta

b - c = (n - p)d, c - a = (p - m)d si a - b = (m - n)d. (23)

In acelasi timp

a = b₁q^m-1, b = b₁q^n-1, c = b₁q^p-1, (24)

unde b₁ si q sunt primul termen si ratia progresiei geometrice.

Se tine seama de egalitatile (23) si (24) si se obtine

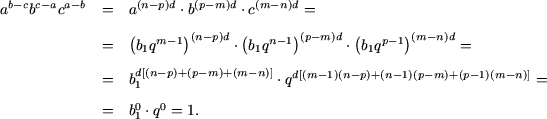
Exemplul 22. Sa se determine triunghiurile, lungimile laturilor carora formeaza o progresie geometrica, iar marimile unghiurilor - o progresiei aritmetica.

Rezolvare. Fie a, b, g - unghiurile interioare ale unui triunghi, opuse laturilor a, b si c. Cum a + b + g = 180^° si a = b - d, g = b + d unde d - ratia progresiei aritmetice, se obtine

b - d + b + b + d = 180^° de unde b = 60^°.

Conform teoremei cosinusurilor

b² = a² + c² - 2accosb. Cum b² = ac, si cosb = ¹/₂, rezulta ac = a² + c² - ac de unde a² - 2ac + c² = 0 sau (a - c)² = 0 si a = c.

Astfel se obtine un triughi isoscel (a = c) cu unghiul cuprins intre aceste laturi egal cu 60^°, adica un triuhgi echilateral.

Exemplul 23. Sirul de numere pozitive a₁, a₂, ..., a_n, ... formeaza o progresie aritmetica, iar sirul b₁, b₂, ..., b_n, ... - o progresie geometrica. Sa se arate ca pentru orice n natural, n > 2

a_n < b_n, daca a₁ š a₂, a₁ = b₁ si a₂ = b₂.

Rezolvare. Fie d - ratia progresiei aritmetice si q - ratia progresiei geometrice. Cum a₁ = b₁ si a₂ = b₂ se obtine

a₁ + d = a₁·q, de unde

si d = a₁(q - 1) > 0. Asadar,

a_n = a₁ + (n - 1)d = a₁ + (n - 1)a₁(q - 1) = a₁(1 + (n - 1)(q - 1))

b_n = b₁q^n-1 = a₁q^n-1

si urmeaza sa demonstram inegalitatea a₁(1 + (n - 1)(q - 1)) < a₁q^n-1 sau, cum a₁ > 0, 1 + (n - 1)(q - 1) < q^n-1. Ultima inegalitate rezulta nemijlocit din inegalitatea lui Bernoulli (a se vedea tema "Principiul Inductiei Matematice" sau "Inegalitati").

Altfel, se considera diferenta

(s-a tinut seama ca

reprezinta suma primilor n - 2 termeni ai progresiei geometrice cu b˘₁ = 1 si q˘ = q).

Cum q > 1 si, prin urmare q^k > 1, k Î N, se obtine

1 + q + q² + ... + q^n-2 - (n - 1) > 0 iar produsul (1 - q)(1 + q + q² + ... + q^n-2 - (n - 1)) < 0. Prin urmare si 1 + (n - 1)(q - 1) - q^n-1 < 0, adica a_n < b_n, n > 2.

Exemplul 24. Sa se determine progresiile ce sunt concomitent si aritmetice si geometrice.

Rezolvare. Fie a₁, a₂, ..., a_n, ... progresiile aritmetica si geometrica. Atunci 2a_k+2 = a_k+1 + a_k+3, si 2a₁q^k+1 = a₁q^k + a₁q^k+2 sau a₁q^k - 2a₁q^k+1 + a₁q^k+2 = 0, de unde se obtine

a₁q^k(1 - 2q + q²) = 0, a₁q^k(1 - q)² = 0.

Asadar, daca a₁q š 0 rezulta q = 1, adica progresia reprezinta un sir constant a₁, a₁, ..., a₁, ... (d = 0, q = 1).

Daca a = 0, se obtine sirul constant 0, 0, ..., 0, ... (d = 0, q Î R), iar daca q = 0, a š 0 solutii nu sunt.

Probleme recapitulative

Fie a₁, a₂, ..., a_n, ... - o progresie aritmetica cu termeni pozitivi. Sa se arate ca
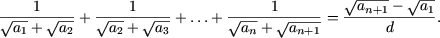
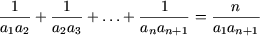
Sa se arate ca unde a₁, a₂, ..., a_n+1, ... sunt termeni nenuli ai unei progresii aritmetice.
Sa se determine numerele de trei cifre, divizibile prin 45, cifrele carora formeaza o progresie aritmetica.
Sa se rezolve ecuatiile 2 + 5 + 8 + 11 + ... + x = 155
Sa se determine suma tuturor numerelor pare de doua cifre.
Sa se afle a₁ + a₆ + a₁₁ + a₁₆ daca a₁, a₂, ..., a_n, ... o progresie aritmetica si a₁ + a₄ + a₇ + ... + a₁₆ = 1447.
Sa se determine valorile lui x pentru care numerele lg2, lg(2^x - 1), lg(2^x + 3) sunt termenii consecutivi ai unei progresii aritmetice.
Sa se arate ca numerele 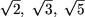nu pot fi termeni ai unei progresii aritmetice.
Fie S_n, S_2n, S_3n respectiv sumele primilor n, 2n, 3n termeni ai aceleiasi progresii geometrice. Sa se arate ca este justa relatia S_n(S_3n - S_2n) = (S_2n - S_n)².
Sa se determine patru numere in progresie aritmetica stiind ca suma lor este 48, iar raportul dintre produsul termenilor extremi si produsul la ceilalti doi termeni este
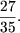
Sa se determine o progresie geometrica, continand sapte termeni, daca suma primilor trei termeni este egala cu 26, iar suma ultimilor trei este egala cu 2106.
Sa se arate ca numerele 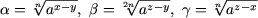formeaza o progresie geometrica.
Sa se determine trei numere, ce formeaza o progresie geometrica, daca suma lor este egala cu 62, iar suma patratelor acestor numere este egala cu 2604.
Numerele a₁, a₂, a₃ formeaza o progresie aritmetica, iar patratele lor o progresie geometrica. Sa se determine aceste numere, daca suma lor este egala cu 21.
Sa se determine progresia aritmetica, daca suma primilor ei zece termeni este egala cu 300, iar primul termen, termenul de rang doi si termenul de rang cinci formeaza o progresie geometrica.

Referinte

P.Cojuhari si altii. Progresii aritmetice si geometrice. Mica biblioteca a elevului. Seria Matematica, informatica. Chisinau, Editura ASRM, 1995.