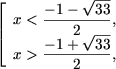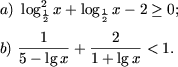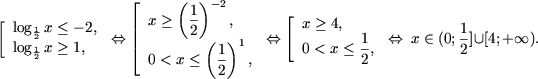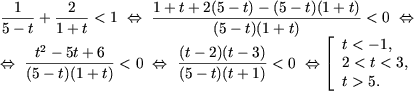| Pagina principala | Ghidul utilizatorului | Rubrica candidatului | Curriculumurile scolare |
| Matematica competitiva | Matematica distractiva| Formule, dictionare | Avizuri |
|Pagini din istorie | Examene, teste | Bibliografie | Link-uri | Site map |

Ecuatia ce contine necunoscuta sub semnul logaritmului sau (si) in baza lui se numeste ecuatie logaritmica.

Cea mai simpla ecuatie logaritmica este ecuatia de tipul

loga x = b.

(1)

Afirmatia 1. Daca a > 0, a ¹ 1, ecuatia (1) pentru orice numar real b are o solutie unica, x = a^b.

Exemplul 1. Sa se rezolve ecuatiile:

a) log₂ x = 3,       b) log₃ x = -1,       c)

Rezolvare. Se utilizeaza afirmatia 1 si se obtine

a) x = 23 sau x = 8;     b) x = 3-1 sau x = 1/3;     c)

sau x = 1.

In continuare vom utiliza frecvent urmatoarele proprietati ale logaritmului:

P1. Identitatea logaritmica de baza

P2. Logaritmul unui produs de factori pozitivi este egal cu suma logaritmilor factorilor:

Nota. Daca N₁·N₂ > 0, atunci proprietatea P2 se scrie

P3. Logarimtul raportului a doua numere pozitive este egal cu diferenta logaritmilor deampartitului si impartitorului:

(a > 0, a ¹ 1, N1 > 0, N2 > 0).

Nota. Daca (echivalent cu N₁N₂ > 0) atunci proprietatea P3 se scrie

(a > 0, a ¹ 1, N1N2 > 0).

P4. Logaritmul puterii unui numar pozitiv este egal cu produsul dintre exponentul puterii si logaritmul acestui numar

Nota. Daca k este par (k = 2s) are loc urmatoarea formula

P5. Formula de trecere de la o baza la alta:

(a > 0, a ¹ 1, b > 0, b ¹ 1, N > 0),

(a > 0, a ¹ 1, b > 0, b ¹ 1).

(2)

Din proprietatile de mai sus rezulta formulele

(a > 0, a ¹ 1, b > 0, c ¹ 0),	(3)
(a > 0, a ¹ 1, b > 0, c ¹ 0),	(4)
(a > 0, a ¹ 1, b > 0, c ¹ 0),	(5)

si daca in (5) c este par (c = 2n) are loc relatia

(b > 0, a ¹ 0, |a| ¹ 1).

(6)

Vom enumera si proprietatile de baza ale functiei logaritmice f(x) = log_a x:

1. Domeniul de definitie al functiei logaritmice este multimea numerelor reale pozitive.
2. Domeniul de valori al functiei logaritmice este multimea numerelor reale.
3. Pentru a > 1 functia logaritmica este strict crescatoare (0 < x₁ < x₂ Þ log_a x₁ < log_a x₂), iar pentru 0 < a < 1, este strict descrescatoare (0 < x₁ < x₂  Þ log_a x₁ > log_a x₂).
4. log_a 1 = 0 si log_a a = 1     (a > 0, a ¹ 1).
5. Daca a > 1 atunci functia logaritmica primeste valori negative pentru x Î (0;1) si valori pozitive pentru x Î (1;+¥), iar daca 0 < a < 1, functia logaritmica ia valori pozitive pentru x Î (0;1) si valori negative pentru x Î (1;+¥).
6. Daca a > 1 functia logaritmica este concava, iar pentru a Î (0;1) functia logaritmica este convexa.

Urmatoarele afirmatii (a se vedea, [1]) sunt utile la rezolvarea ecuatiilor logaritmice:

Afirmatia 2. Ecuatia log_a f(x) = log_a g(x)     (a > 0, a ¹ 1) este echivalenta cu unul din sistemele (evident, se alege acel sistem, inecuatia caruia se rezolva mai simplu)

	f(x) = g(x),			f(x) = g(x),
	f(x) > 0,			g(x) > 0.

Afirmatia 3. Ecuatia log_h(x) f(x) = log_h(x) g(x) este echivalenta cu unul din sistemele

	f(x) = g(x),			f(x) = g(x),
	h(x) > 0,			h(x) > 0,
	h(x) ¹ 1,			h(x) ¹ 1,
	f(x) > 0,			g(x) > 0.

Tinem sa mentionam ca in procesul rezolvarii ecuatiilor logaritmice adesea se aplica transformari ce modifica domeniul de valori admisibile (DVA) al ecuatiei initiale. Prin urmare pot aparea solutii "straine" sau pot fi pierdute unele solutii. De exemplu ecuatiile

Prin urmare la rezolvarea ecuatiilor logaritmice este util de folosit in DVA transformari echivalente. In caz contrar verificarea solutiilor este parte componenta a rezolvarii. In plus, se tine seama de transformarile ce pot aduce la pierderea solutiilor.

In continuare vom considera cele mai frecvente metode de rezolvare a ecuatiilor logaritmice.

Exemplul 2. Sa se rezolve ecuatiile:

a) log2(5 + 3log2(x - 3)) = 3,	c) log(x - 2)9 = 2,
b)	d) log2x + 1(2x2 - 8x + 15) = 2.

Rezolvare. a) Logaritm a numarului pozitiv b in baza a (a > 0, a ¹ 1) se numeste exponentul puterii, la care trebuie ridicat a ca sa obtinem b. Asadar log_ab = c Û b = a^c si, prin urmare,

Verificarea este parte componenta a rezolvarii acestei ecuatii:

Se obtine 3 = 3 si prin urmare x = 5 este solutie a acestei ecuatii.

b) Similar exemplului a) se obtine ecuatia

Se reduce la rezolvarea ecuatiei liniare x - 3 = 3(x + 3) de unde rezulta x = -6. Se efectueaza verificarea si se obtine ca x = -6 este solutia ecuatiei initiale.

c) Similar exemplului a) se obtine ecuatia

d) Se aplica definitia logaritmului si se obtine ecuatia

Exemplul 3. Sa se rezolve ecuatiile

Rezolvare. a) DVA al ecuatiei x Î (0;+¥) se determina rezolvand sistemul (conditia de existenta a logaritmilor ce sunt prezenti in ecuatie)

	x > 0,
	x+3 > 0,
	x+24 > 0.

Se aplica proprietatea P2 si afirmatia 1 si se obtine

log3x + log3(x + 3) = log3(x + 24)   Û

log3x(x + 3) = log3(x + 24), x > 0,

Û

Û   x(x + 3) = x + 24, x > 0,

Û   x2 + 2x - 24 = 0, x > 0,

Û   x1 = -6, x2 = 4, x > 0,

Û   x = 4.

b) Se utilizeaza proprietatea P3 si se obtine o consecinta a ecuatiei initiale

c) DVA: x Î (0;+¥). Se utilizeaza proprietatea P5 si se obtine ecuatia

d) DVA al ecuatiei se obtine rezolvand sistemul

	x-2 > 0,
	(x - 4)2 ¹ 0,

Se utilizeaza proprietatea P2 si pe DVA se obtine ecuatia echivalenta

	x2 - 6x + 8 = 1,
	x2 - 6x + 8 = -1,

e) Cum

In unele cazuri ecuatia logaritmica poate fi redusa la o ecuatie algebrica relativ la o necunoscuta noua. De exemplu, ecuatia F(log_ax) = 0, unde F(x) este o functie algebrica rationala, prin intermediul substitutiei log_ax = t se reduce la o ecuatie algebrica in raport cu t, R(t) = 0.

Exemplul 4. Sa se rezolve ecuatiile:

a) lg2x - 3lgx + 2 = 0,	c) lg2100x + lg210x + lgx = 14,
b) ,	d) 5lgx = 50 - xlg5.

Rezolvare. a) DVA al ecuatiei este x Î (0;+¥). Se noteaza lgx = t, atunci lg²x = (lg x)² = t² si se obtine ecuatia patrata

	lg x = 1,
	lg x = 2,

b) DVA al ecuatiei este multimea (1;+¥). Cum prin substitutia t = log₂(x - 1) se obtine ecuatia patrata

log2(x - 1) = -1/4, log2(x - 1) = 1,

Û

Û

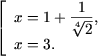
c) DVA al ecuatiei este multimea (0;+¥). Cum

d) DVA al ecuatiei este x Î (0;1)È(1;+¥). Cum ecuatia devine 5^{lg x} = 50 - 5^{lg x} sau 2·5^{lg x} = 50, de unde 5^{lg x} = 25 sau 5^{lg x} = 5²   Û   lgx = 2   Û   x = 100.

IV. Ecuatii ce contin expresii de tipul

Exemplul 5. Sa se rezolve ecuatiile:

Rezolvare. a) DVA al acuatiei se determina din sistemul

	x+2 > 0,
	x + 2 ¹ 1,

	log2(x + 2) = -1,
	log2(x + 2) = 2,

	x + 2 = 1/2,
	x + 2 = 4

	x1 = -3/2,
	x2 = 2.

b) DVA al ecuatiei x Î (0;1)È(1;+¥). Cum (a se vedea proprietatea P5 si formula (2))

ecuatia devine

sau

Se logaritmeaza ambii membri ai ecuatiei in baza 2 si se obtine

Exemplul 6. Sa se rezolve ecuatiile

a) 2x = 9 - log3x;

b)

c) log2(x2 + 1) - log2x = 2x - x2;

d) log5(x + 2) = 4 - x;

e)

f) |log2(3x - 1) - log23| = |log2(5 - 2x) - 1|;

g) logx+1(x3 - 9x + 8)logx-1(x + 1) = 3;

h) log2(6x - x2 - 5) = x2 - 6x + 11.

Rezolvare. a) Se observa ca x = 3 este solutie a acestei ecuatii: 2³ = 9-log₃3, 8 = 9-1, 8 = 8. Alte solutii ecuatia nu are. In adevar, membrul din stanga ecuatiei reprezinta o functie strict crescatoare, iar cel din dreapta - o functie strict descrescatoare si, prin urmare, graficele acestor functii pot avea cel mult un punct comun. Cum x = 3 este solutie, rezulta ca altele nu sunt.

b) DVA al ecuatiei x Î (1;+¥). Se noteaza log₃(x-1) = t si se obtine o ecuatie patrata in t

si

	log3(x - 1) = -4,
	log3(x - 1) = 4/x.

c) DVA al ecuatiei se determina din sistemul

	x2 + 1 > 0,
	x > 0,

Cum pentru x > 0 iar semnul egalitatii se obtine doar pentru x = 1, rezulta ca membrul din stanga, In acelas timp membrul din dreapta ecuatiei are valoarea maxima 1 pentru x = 1 (varful parabolei y = 2x - x² se afla in punctul (1;1)). Astfel ecuatia are solutii numai in cazul cand 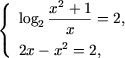adica x = 1.

d) Se rezolva similar exemplului a) si se obtine x = 3.

e) Se utilizeaza teorema A1 din ecuatii irationale si se obtine

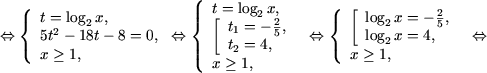
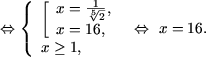
f) Se utilizeaza proprietatea P3, P2 si proprietatile modulului (a se vedea, de exemplu [2]) si se obtine

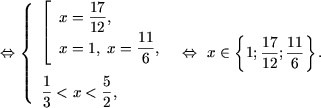
g) Se determina DVA al ecuatiei

	x + 1 > 0,	Û	x > -1,			Û
	x + 1 ¹ 1,		x ¹ 0,	Û	x > 1,
	x3 - 9x + 8 > 0,		x3 - x - 8x + 8 > 0,		x ¹ 2,
	x - 1 > 0,		x > 1,		(x - 1)(x2 + x - 8) > 0,
	x - 1 ¹ 1,		x ¹ 2,

Û x > 1, x ¹ 2, x2 + x - 8 > 0,

Û x > 1, x ¹ 2,

Û

Se aplica proprietatea P5 si se obtine (pe DVA)

	x = 1,
	x2 + x - 8 = x2 - 2x + 1,

Cum x = 1 nu verifica DVA si 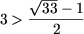ramane numai x = 3.

h) Cum functia f(x) = 6x - x² - 5 isi atinge maximul 4 pentru x = 3, rezulta

Inecuatia ce contine necunoscuta sub semnul logaritmului se numeste logaritmica.

In procesul rezolvarii inecuatiilor logaritmice se aplica frecvent urmatoarele afirmatii referitor echivalenta ecuatiilor si se tine seama de proprietatea de monotonie a functiei logaritmice (a se vedea de exemplu [1]).

Afirmatia 1. Daca a > 1, inecuatia log_a f(x) > log_a g(x) este echivalenta cu sistemul de inecuatii

	f(x) > g(x),
	g(x) > 0.

Afirmatia 2. Daca 0 < a < 1, inecuatia log_a f(x) > log_a g(x) este echivalenta cu sistemul de inecuatii

	f(x) < g(x),
	f(x) > 0.

Afirmatia 3. Inecuatia log_h(x) f(x) > log_h(x) g(x) este echivalenta cu totalitatea sistemelor de inecuatii:

		h(x) > 1,
		f(x) > g(x) > 0,
		0 < h(x) < 1,
		0 < f(x) < g(x).

Mentionam, ca in inecuatia log_a f(x) > log_a g(x) in locul semnului > poate sa figureze unul din semnele ³ ,   < ,  £ . In asa caz afirmatiile 1-3 se modifica respectiv.

Exemplul 1. Sa se rezolve inecuatiile

a) log3(x2 - x) ³ log3(x + 8);	d)
b)	e) log2x(x2 - 5x + 6) < 1.
c)

Rezolvare. a) Se aplica afirmatia 1 si se obtine

log3(x2 - x) ³ log3(x + 8) Û	x2 - x ³ x + 8,	Û	x2 - 2x - 8 ³ 0,	Û
	x+8 > 0,		x > -8,

Û		x £ -2,
		x ³ 4,	Û   x Î (-8;-2]È[4;+¥).
		x > -8,

b) Baza logaritmului din inecuatie este un numar intre zero si unu, se aplica afirmatia 2 si se obtine

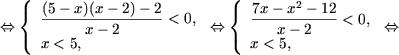
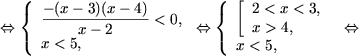
c) Se scrie 0 = log₂1 si se aplica afirmatia 1

Se scrie si se aplica afirmatia 2 si se rezolva sistemul obtinut

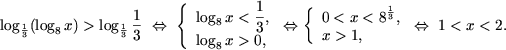
d) Se aplica afirmatia 3 si se obtine

Û	x Î (3;4),	Û   x Î (3;4).
	x Î Æ,

Rezolvarea primului sistem al totalitatii

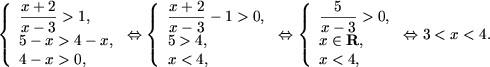
Rezolvarea ultimului sistem al totalitatii

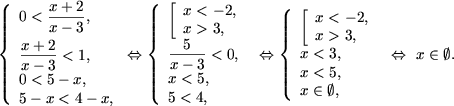
e) Se scrie 1 = log_2x2x, se aplica afirmatia 3 si se tine seama ca semnul > este inlocuit cu <; .

log2x(x2 - 5x + 6) < log2x2x   Û		2x > 1,
		x2 - 5x + 6 < 2x,
		x2 - 5x + 6 > 0,
		0 < 2x < 1,
		x2 - 5x + 6 > 2x,
		2x > 0,

Û	x Î (1;2)È(3;6),	x Î (0;1/2)È(1;2)È(3;6).
	x Î (0;1/2)

Rezolvarea primului sistem al totalitatii

		x > 1/2,	Û		x > 1/2,	Û   x Î (1;2)È(3;6).
		x2 - 7x + 6 < 0,			1 < x < 6,
		x < 2,			x < 2,
		x > 3,			x > 3,

Rezolvarea ultimului sistem al totalitatii

0 < x < 1/2, x2 - 7x + 6 > 0,

Û 0 < x < 1/2, x < 1, x > 6,

Û   x Î (0;1/2).

Inecuatia de tipul F(log_ax) > 0, se reduce prin intermediul substitutiei t = log_ax la inecuatia algebrica F(t) > 0. Se rezolva inecuatia F(t) > 0, iar apoi se rezolva ecuatiile logaritmice simple ce se obtin. Bineanteles aceeasi se refera si la inecuatiile similare ce se obtin din cea precedenta, inlocuind in locul semnului > unul din semnele < , £, ³ .

Exemplul 2. Sa se rezolve inecuatiile

Rezolvare. a) Se noteaza si se rezolva inecuatia patrata t² + t - 2 ³ 0, de unde rezulta t £ -2 sau t ³ 1. Asadar se obtine totalitatea, ce se rezolva astfel:

b) Se noteaza t = lgx si se obtine inecuatia rationala

ce se rezolva utilizand metoda intervalelor (a se vedea de exemplu [1], [2])

Se revine la variabila initiala si se obtine

	lgx < -1,			0 < x < 1/10,
	2 < lgx < 3,	Û		100 < x < 1000,	Û   x Î (0;1/10)È(100;1000)È(105;+¥).
	lgx > 5,			x > 105,

In cazul inecuatiilor logaritmice ce nu au forma celor din afirmatiile 1-3, se determina DVA si prin transformari ce pastreaza echivalenta se reduc la inecuatii ce se rezolva cu ajutorul echivalentelor 1-3.

Exemplul 3. Sa se rezolve inecuatiile

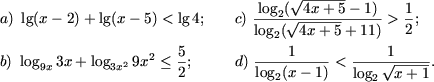
Rezolvare. a) DVA al inecuatiei este multimea (5;+¥). Se aplica proprietatea P2 si se obtine inecuatia

	(x - 2)(x - 5) < 4,
	(x - 2)(x - 5) > 0.

		x2 - 7x + 6 < 0,				1 < x < 6,
		x < 2,	Û			x < 2,	Û   x Î (1;2)È(5;6).
		x > 5,				x > 5,

e) DVA al inecuatiei se determina din sistemul

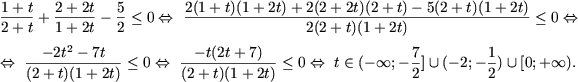
Asadar, revenind la variabila initiala se obtine totalitatea de inecuatii logaritmice simple

c) DVA al inecuatiei se obtine rezolvand sistemul

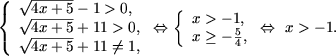
Cum inecuatia este echivalenta cu inecuatia

Se tine seama de DVA si se obtine raspunsul x Î (5;+¥).

d) Se utilizeaza metoda intervalelor generalizata: (DVA   x Î (1;2)È(2;+¥)).

Cum in DVA   log₂(x-1) > 0 pentru x > 2 si log₂(x-1) < 0 pentru 1 < x < 2, pentru orice x din DVA, pentru x Î (1;2)È(2;3) si pentru x > 3,

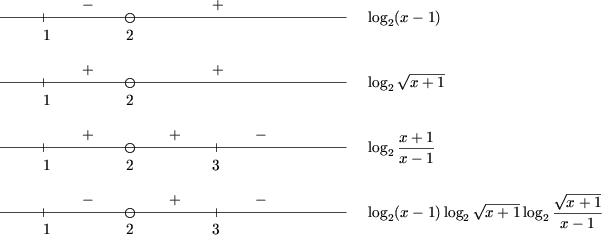
se obtine x Î (1;2)È(3;+¥).

Pentru consolidarea deprinderilor de rezolvare a ecuatiilor si inecuatiilor logaritmice se recomanda a consulta de exemplu problemarele [3-5].

| Pagina principala | Ghidul utilizatorului | Rubrica candidatului | Curriculumurile scolare |
| Matematica competitiva | Matematica distractiva| Formule, dictionare | Avizuri |
|Pagini din istorie | Examene, teste | Bibliografie | Link-uri | Site map |

---