
| Pagina principala |
Ghidul utilizatorului |
Rubrica candidatului |
Curriculumurile scolare |
| Matematica competitiva |
Matematica distractiva|
Formule, dictionare |
Avizuri |
|Pagini din istorie |
Examene, teste |
Bibliografie |
Link-uri |
Site map |
Inecuatii irationale
Inecuatia ce contine necunoscuta sub semnul radicalului se numeste
inecuatie irationala.
La rezolvarea inecuatiilor irationale, de regula, este necesar de
a ridica la putere ambii membri ai inecuatiei. Astfel de
transformari pot aduce la inecuatii neechivalente cu cea initiala
si intrucat multimea solutiilor unei inecuatii reprezinta in
majoritatea cazurilor o multime infinita, verificarea ei este
dificila. Unica metoda ce garanteaza justetea raspunsului consta
in faptul, ca in procesul rezolvarii inecuatiilor irationale
urmeaza a fi efectuate numai astfel de transformari, ce pastreaza
echivalenta lor. In legatura cu aceasta vom aduce afirmatiile
respective, care sunt frecvent utilizate la rezolvarea
inecuatiilor irationale (in toate afirmatiile n este un numar
natural).
A1. Inecuatia
 este echivalenta cu totalitatea sistemelor de inecuatii
este echivalenta cu totalitatea sistemelor de inecuatii

|

|
g(x) < 0, |
| f(x) ³ 0, |

|
g(x) ³ 0, |
|
f(x) > [g(x)]2n.
|
Nota. Din afirmatia A1 rezuta ca inecuatia
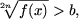 pentru b ³ 0 este echivalenta cu inecuatia
f(x) > [b]2n,
iar pentu b < 0, este echivalenta cu inecuatia
f(x) ³ 0.
pentru b ³ 0 este echivalenta cu inecuatia
f(x) > [b]2n,
iar pentu b < 0, este echivalenta cu inecuatia
f(x) ³ 0.
A2. Inecuatia
 este echivalenta cu sistemul de inecuatii
este echivalenta cu sistemul de inecuatii

|
g(x) > 0,
|
|
f(x) ³ 0,
|
|
f(x) < [g(x)]2n.
|
Nota. In particular, daca membrul din dreapta inecuatiei
reprezinta un numar b (g(x) = b),
din afirmatia A2 rezulta:
- daca b > 0,
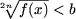 Û 0 £
f(x) < [b]2n
Û 0 £
f(x) < [b]2n
|
- daca b £ 0, inecuatia
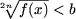 nu are solutii.
nu are solutii.
|
A3. Inecuatia
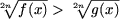 este echivalenta cu sistemul de inecuatii
este echivalenta cu sistemul de inecuatii

|
f(x) > g(x), |
|
g(x) ³ 0.
|
A4. Inecuatia
 este echivalenta cu sistemul
este echivalenta cu sistemul

|
f(x) > [g(x)]2n,
|
|
g(x) > 0.
|
A5. Inecuatia
 este echivalenta cu totalitatea de sisteme de inecuatii
este echivalenta cu totalitatea de sisteme de inecuatii

|

|
g(x) < 0,
|
|
f(x) ³ 0,
|

|
g(x) > 0,
|
|
f(x) ³ 0,
|
|
f(x) < [g(x)]2n.
|
A6. Inecuatia
 este echivalenta cu totalitatea
este echivalenta cu totalitatea

|

|
f(x) = 0,
|
|
x Î D(g),
|

|
f(x) > 0,
|
|
g(x) ³ 0,
|
unde D(g) desemneaza domeniul de definitie al
functiei g.
A7. Inecuatia
 este echivalenta cu totalitatea
este echivalenta cu totalitatea

|

|
f(x) = 0,
|
|
x Î D(g),
|

|
f(x) > 0,
|
|
g(x) £ 0.
|
A8. Inecuatiile
 si f(x) <
[g(x)]2n+1
sunt echivalente.
si f(x) <
[g(x)]2n+1
sunt echivalente.
A9. Inecuatiile
 si f(x) >
[g(x)]2n+1
sunt echivalente.
si f(x) >
[g(x)]2n+1
sunt echivalente.
Nota. Daca m este impar, atunci
f(x) < g(x) Û
[f(x)]m <
[g(x)]m,
f(x) > g(x) Û
[f(x)]m >
[g(x)]m,
adica la ridicare la putere impara semnul inecuatiei se pastreaza.
Sa analizam cateva exemple.
Exemplul 1. Sa se rezolve inecuatiile
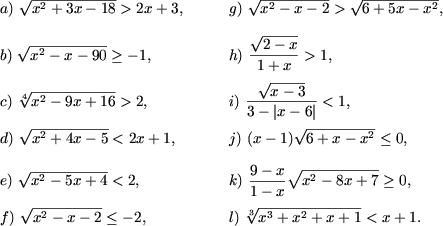
Rezolvare.
a) Se aplica afirmatia A1 (in cazul dat
f(x) = x2 + 3x - 18, iar
g(x) = 2x + 3) si se obtine:
 >
2x + 3 >
2x + 3
|
|
Û

|

|
x2 + 3x - 18 ³ 0,
|
|
2x + 3 < 0,
|

|
x2 + 3x - 18 > (2x + 3)2,
|
|
2x + 3 ³ 0,
|
|
Û

|
x Î (-¥,-6],
|
|
x Î Æ,
|
|
Û |
Û x Î
(-¥,-6].
In adevar, cum
x2 + 3x - 18 ³ 0
Û
(x + 6)(x - 3) ³ 0,
solutiile primei inecuatii formeaza multimea
x Î
(-¥;-6]È[3;+¥),
si cum x Î
(-¥,-3/2) sunt solutiile
celei de a doua inecuatie a sistemului, se obtine ca solutia
primului sistem de inecuatii este multimea x
Î (-¥,-6].
Prima inecuatie a sistemului al doilea din totalitate nu are solutii:
x2 + 3x - 18 > (2x + 3)2
Û
x2 + 3x - 18 >
4x2 + 12x + 9
Û
Û
3x2 + 9x + 27 < 0
Û
x2 + 3x + 9 < 0
Û
x Î Æ
si, prin urmare, al doilea sistem este incompatibil.
Asadar, multimea solutiilor inecuatiei initiale este
(-¥,-6].
b) Se observa ca membrul din dreapta inecuatiei este un numar
negativ, iar membrul din stanga de indata ce exista (conditia
x2 - x - 90 ³ 0)
ia valori nenegative. Se tine seama de nota la afirmatia
A1
si solutiile inecuatiei initiale se obtin rezolvand inecuatia
x2 - x - 90 ³ 0,
sau
(x + 9)(x - 10) ³ 0,
de unde x Î
(-¥,-9]È[10,+¥).
c) Se tine seama de nota la afirmatia
A1, se ridica ambii membri
ai inecuatiei (nenegativi pe DVA) la puterea a patra si se
obtine inecuatia echivalenta:
x2 - 9x + 16 > 16,
sau
x2 - 9x > 0,
cu solutiile x Î
(-¥,0)È(9,+¥).
d) Se utilizeaza afirmatia A2
(aici f(x) = x2 + 4x - 5 si
g(x) = 2x - 3) si se obtine
 < 2x + 1 < 2x + 1
|
|
Û

|
2x + 1 ³ 0,
|
|
x2 + 4x - 5 ³ 0,
|
|
x2 + 4x - 5 < (2x + 1)2,
|
|
Û

|
|
x ³ -1/2,
|

|
x £ -5,
|
|
x ³ 1,
|
|
3x2 + 6 > 0,
|
|
Û
|
Û

|
x ³ 1,
|
Û
x ³ 1.
|
|
x Î R,
|
e) Se tine seama de nota la afirmatia
A2 si se obtine
 < 2 < 2
|
|
Û

|
x2 - 5x + 4 < 4,
|
|
x2 - 5x + 4 ³ 0,
|
|
Û

|
x2 - 5x < 0,
|
|
x2 - 5x + 4 ³ 0
|
|
Û

|
|
0 < x < 5,
|

|
x £ 1,
|
|
x ³ 4,
|
|
Û
|
Û
x Î (0;1]È[4;5).
f) Inecuatia nu are solutii, deoarece membrul din stanga
inecuatiei pe DVA reprezinta o expresie valorile careia sunt
numere nenegative si, prin urmare, nu poate fi mai mic sau egal cu un
numar negativ.
g) Se aplica afirmatia
A3 (aici f(x) =
x2 - x - 2 si
g(x) = 6 + 5x - x2) si se obtine:
 > >

|
|
Û

|
x2 - x - 2 > 6 + 5x - x2,
|
|
6 + 5x - x2 ³ 0,
|
|
Û

|
x2 - 3x - 4 > 0,
|
|
x2 - 5x - 6 £ 0,
|
|
Û
|
Û

|

|
x < -1,
|
Û
x Î (4,6].
|
|
x > 4,
|
|
-1 £ x £ 6,
|
h) Se utilizeaza afirmatia A4 si se obtine:
|
|
Û

|
2 - x > (x + 1)2,
|
|
x + 1 > 0,
|
|
Û

|
x2 + 3x - 1 < 0,
|
|
x > -1,
|
|
Û
|

i) Conform afirmatiei
A5 se obtine totalitatea de sisteme de
inecuatii:

|

|
3 - |x - 6| < 0,
|
|
x - 3 ³ 0,
|

|
3 - |x - 6| > 0,
|
|
x - 3 ³ 0,
|
|
x - 3 < (3 - |x - 6|)2.
|
Rezolvand primul sistem, se obtine:

|
|x - 6| > 3,
|
|
x ³ 3,
|
|
Û

|

|
x - 6 > 3,
|
Û

|

|
x > 9,
|
Û
x > 9.
|
|
x - 6 < -3,
|
x < 3,
|
|
x ³ 3,
| |
x ³ 3,
|
Rezolvand al doilea sistem al totalitatii, se obtine:

|
|x - 6| < 3,
|
Û

|
-3 < x - 6 < 3,
|
Û
|
|
x ³ 3,
|
x ³ 3,
|
|
x - 3 < 9 - 6|x - 6| + x2 - 12x + 36,
|
x2 - 6|x - 6| - x + 48 > 0,
|
Û

|
3 < x < 9,
|
|
x2 - 6|x - 6| - x + 48 > 0,
|
|
Û

|

|
3 < x £ 6,
|
Û
|
|
x2 + 6(x - 6) - x + 48 > 0,
|

|
6 < x < 9,
|
|
x2 - 6(x - 6) - x + 48 > 0,
|
|
Û

|

|
3 < x £ 6,
|
Û

|

|
3 < x £ 6,
|
Û
3 < x < 9.
|
|
x2 + 5x + 12 > 0,
|
x Î R
|

|
6 < x < 9,
|

|
6 < x < 9,
|
|
x2 - 7x + 84 > 0,
|
x Î R,
|
asadar, solutiile inecuatiei initiale sunt:
x Î
(3;9)È(9;+¥).
j) Se tine seama de afirmatia A7 si se obtine:
(x - 1) £ 0
£ 0
|
|
Û

|

|
6 + x - x2 = 0,
|
Û
|
|
x Î R.
|

|
6 + x - x2 > 0,
|
|
x - 1 £ 0,
|
Û

|

|
x = -2,
|
Û
x Î [-2;1]È{3}.
|
|
x = 3,
|

|
-2 < x < 3,
|
|
x £ 1,
|
k) Se utilizeaza afirmatia A6 si se obtine:

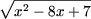 ³ 0
³ 0
|
|
Û

|

|
x2 - 8x + 7 = 0,
|
Û
|
|
x ¹ 1,
|

|
x2 - 8x + 7 > 0,
|
 ³ 0,
³ 0,
|
Û

|

|

|
x = 1,
|
Û

| |
x = 7,
|

|
x < 1,
|
|
x ³ 9,
|
|
Û x Î
(-¥,1)È{7}È[9,+¥).
|
|
x = 7,
|
|
x ¹ 1,
|

|

|
x < 1,
|
|
x > 7,
|

|
x ³ 9,
|
|
x < 1,
|
l) Se ridica ambii membri ai inecuatiei la cub (afirmatia
A9) si
se obtine inecuatia echivalenta:
x3 + x2 + x + 1 <
x3 + 3x2 + 3x + 1
sau
2x2 + 2x > 0,
de unde x < -1 sau x > 0.
In continuare vom ilustra metoda substitutiei.
Exemplul 2. Sa se rezolve inecuatiile

Rezolvare. a) Se noteaza
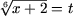 (t ³ 0),
atunci
(t ³ 0),
atunci  si inecuatia devine
si inecuatia devine
3t - t2 ³ 2,
sau
t2 - 3t + 2 £ 0,
cu solutiile
1 £ t £ 2.
Revenind la necunoscuta initiala si utilizand notele la
afirmatiile A1 si A2, se obtine

b) Se noteaza
 t ³ 0 si se utilizeaza
metoda intervalelor (a se vedea, de ex. [1],
[2]):
t ³ 0 si se utilizeaza
metoda intervalelor (a se vedea, de ex. [1],
[2]):
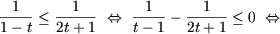

Cum t ³ 0,
rezulta 2t + 1 ³ 1 si, prin urmare,
ultima inecuatie este echivalenta cu sistemul

|
t = 0,
|
|
1 - t < 0,
|
de unde rezulta t = 0 si t > 1. Se revine la necunoscuta
initiala si se obtine:
 sau x = -1 si x > 0. Astfel
x Î
{-1}È(0,+¥).
sau x = -1 si x > 0. Astfel
x Î
{-1}È(0,+¥).
c) Se observa ca inecuatia contine expresii reciproc inverse. Se
noteaza
 atunci
atunci
 si inecuatia devine
si inecuatia devine

Cum t > 0, se multiplica ambii membri ai inecuatiei cu t
si se obtine inecuatia echivalenta
t2 - t - 2 < 0,
cu solutiile -1 < t < 2. Deoarece t > 0,
ramane 0 < t < 2, sau

Ultima inecuatie este echivalenta cu sistemul
 sau
sau

|
Û

|

|
x > 8/3,
|
|
x < 2,
|

|
x < 0,
|
|
x > 2,
|
|
de unde x Î
(-¥;0)È(8/3;+¥).
d) Inecuatia se scrie (se aduna 25 si se scade 25)

Se noteaza
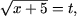 atunci x + 5 = t2, si se obtine
inecuatia patrata
atunci x + 5 = t2, si se obtine
inecuatia patrata
5t2 - 17t + 6 < 0,
de unde
2/5 < t < 3,
sau

Cum toti membrii inecuatiei duble sunt pozitivi se ridica la
patrat si se obtine inecuatia echivalenta
4/25 < x + 5 < 9,
de unde x Î
(-421/25;4).
e) DVA al inecuatiei este x ³ 1.
Pe DVA inecuatia este echivalenta cu inecuatia
 sau
sau

Se noteaza
 si se obtine inecuatia patrata
si se obtine inecuatia patrata
18 - 9t - 2t2 ³ 0
cu solutiile -6 £ t £ 3/2. Cum t ³ 0 ecuatia initiala este echivalenta cu
urmatoarea

Se utilizeaza notele la afirmatia
A1 si A2 si se obtine:
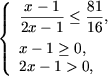 de unde x ³ 1.
de unde x ³ 1.
f) Se noteaza
 atunci x - 1 = t2 si
atunci x - 1 = t2 si
 si inecuatia devine
si inecuatia devine
 sau
sau

Se ridica la cub si se obtine (afirmatia
A9) ecuatia echivalenta
1 - t2 > (1 - t)3,
sau
|
(1 - t)(1 + t) - (1 - t)3 > 0,
|
|
(1 - t)(1 + t - (1 - t)2) > 0,
|
|
(1 - t)(1 + t - 1 + 2t - t2) > 0,
|
|
(1 - t)t(3 - t) > 0.
|
Cum t ³ 0 ramane

|
(1 - t)(3 - t) > 0,
|
|
t ¹ 0,
|
de unde rezulta totalitatea

| |
t > 3,
|

|
t < 1,
|
|
t ¹ 0,
|
sau
 de unde
de unde

|
x - 1 > 9,
|
|
0 < x - 1 < 1,
|
sau

|
x > 10,
|
|
1 < x < 2.
|
adica x Î
(1;2)È(10;+¥).
O metoda frecventa de rezolvare a inecuatiilor irationale consta
in reducerea lor (cu ajutorul unor transformari ce pastreaza
echivalenta inecuatiilor) la inecuatii de tipul celor ce figureaza
in afirmatiile
A1-A9,
se aplica afirmatia respectiva si tinand seama de DVA al
inecuatiei se obtine multimea solutiilor.
Exemplul 3. Sa se rezolve inecuatiile

Rezolvare. a) DVA al inecuatiei x Î [- 1/2;2] se determina
rezolvand sistemul de inecuatii (conditiile de existenta ale
radicalilor de ordinul doi)

|
x + 4 ³ 0,
|
|
2x + 1 ³ 0,
|
|
2 - x ³ 0.
|
Inecuatia se scrie astfel

Acum ambii membri ai inecuatiei sunt pozitivi pe DVA si
ridicand la patrat se obtine inecuatia echivalenta:
 sau
sau

Iar ridicand la patrat si tinand seama de DVA obtinem

|
1 < 4(2 - x)(2x + 1),
|
|
-1/2 £ x
£ 2,
|
sau

|
8x2 - 12x - 7 < 0,
|
|
-1/2 £
x £ 2,
|
de unde

b) Inecuatia se scrie astfel:
 sau
sau

Cum 1 + x3 =
(1 + x)(1 - x + x2) si cum
1 - x + x2 > 0 pentu orice x Î R inecuatia
 este echivalenta cu urmatoarea
este echivalenta cu urmatoarea

Se divide cu
 (aceasta expresie ia numai valori mai mari ca zero, oricare n-ar fi
x, deoarece discriminantul trinomului
1 - x + x2 este negativ
(D = 1 - 4 = -3 < 0)
iar coeficientul de pe langa x2 este pozitiv
(a = 1)) si se obtine inecuatia
(aceasta expresie ia numai valori mai mari ca zero, oricare n-ar fi
x, deoarece discriminantul trinomului
1 - x + x2 este negativ
(D = 1 - 4 = -3 < 0)
iar coeficientul de pe langa x2 este pozitiv
(a = 1)) si se obtine inecuatia
 echivalenta cu totalitatea sistemelor de inecuatii
echivalenta cu totalitatea sistemelor de inecuatii
 sau, tinand seama de afirmatia A3,
sau, tinand seama de afirmatia A3,

|

|
1 + x ³ 1 - x + x2,
|
|
1 - x + x2 ³ 0,
|
|
x > 1,
|

|
1 + x £ 1 - x + x2,
|
|
1 + x ³ 0,
|
|
x < 1,
|
de unde rezulta

|

|
x2 - 2x £ 0,
|
|
x Î R,
|
|
x > 1,
|

|
x2 - 2x ³ 0,
|
|
x > -1,
|
|
x < 1,
|
|
Û

|
1 < x £ 2,
|
|
-1 < x £ 0.
|
|
Asadar, multimea solutiilor inecuatiei initiale este
x Î (-1;0]È(1;2].
c) DVA al inecuatiei x Î
[-1;0)È[1;+¥)
se determina din sistemul de inecuatii:

Inecuatia se scrie astfel
 sau, utilizand urmatoarea proprietate a radicalilor de ordin par:
sau, utilizand urmatoarea proprietate a radicalilor de ordin par:
 (AB ³ 0), se obtine
(AB ³ 0), se obtine

Ultima inecuatie, tinand seama ca in DVA x + 1
³ 0 si
 si deci |x + 1| = x + 1,
si deci |x + 1| = x + 1,
 este echivalenta cu sistemul
este echivalenta cu sistemul
 care se rezolva astfel:
care se rezolva astfel:





d) Se noteaza
 atunci
atunci
 de unde
de unde
 si inecuatia devine
si inecuatia devine
t + t2 - 5 < 51
sau
t2 + t - 56 < 0,
cu solutiile -8 < t < 7. Cum t > 0 (ca suma
a doi radicali de ordin par) ramane t < 7, sau

Ultima inecuatie se poate rezolva similar exemplului
3a):
 + +
 < 7 < 7
|
Û

|
x - 1 + 2  + x + 6 < 49, + x + 6 < 49,
|
|
x-1 ³ 0,
|
|
x+6 ³ 0,
|
|
Û
|
|
|
Û

|
(x-1)(x+6) < (22-x)2,
|
|
22-x > 0,
|
|
x ³ 1,
|
|
Û
|
Û

|
x < 10,
|
Û 1 £ x < 10,
|
|
1 £ x < 22,
|
sau astfel: se observa ca pentru x = 10,
 + +
 = 7,
prin urmare cum functia f(x) = = 7,
prin urmare cum functia f(x) =
 + +
 este o functie crescatoare pentru x ³ 10
inecuatia nu are solutii. Ramane sa tinem seama de
DVA: x ³ 1 si sa scriem
multimea solutiilor: x Î [1;10).
este o functie crescatoare pentru x ³ 10
inecuatia nu are solutii. Ramane sa tinem seama de
DVA: x ³ 1 si sa scriem
multimea solutiilor: x Î [1;10).
e) Cum
 inecuatia se scrie astfel:
inecuatia se scrie astfel:
 sau, tinand seama ca
sau, tinand seama ca


Cum  rezulta
rezulta
 si prin urmare
si prin urmare
 Asadar
Asadar
 sau
sau

Cum |a| ³ -a,
oricare n-ar fi a, rezulta ca multimea solutiilor inecuatiei
date coincide cu DVA, adica x ³ 4.
Exercitii de recapitulare
| Pagina principala |
Ghidul utilizatorului |
Rubrica candidatului |
Curriculumurile scolare |
| Matematica competitiva |
Matematica distractiva|
Formule, dictionare |
Avizuri |
|Pagini din istorie |
Examene, teste |
Bibliografie |
Link-uri |
Site map |

|
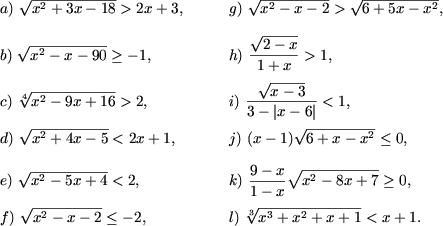


![]() (t ³ 0),
atunci
(t ³ 0),
atunci ![]() si inecuatia devine
si inecuatia devine
![]() t ³ 0 si se utilizeaza
metoda intervalelor (a se vedea, de ex. [1],
[2]):
t ³ 0 si se utilizeaza
metoda intervalelor (a se vedea, de ex. [1],
[2]):
![]() atunci
atunci
![]() si inecuatia devine
si inecuatia devine


![]() atunci x + 5 = t2, si se obtine
inecuatia patrata
atunci x + 5 = t2, si se obtine
inecuatia patrata
![]() si se obtine inecuatia patrata
si se obtine inecuatia patrata
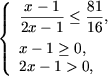
![]() atunci x - 1 = t2 si
atunci x - 1 = t2 si
![]() si inecuatia devine
si inecuatia devine



![]() (aceasta expresie ia numai valori mai mari ca zero, oricare n-ar fi
x, deoarece discriminantul trinomului
1 - x + x2 este negativ
(D = 1 - 4 = -3 < 0)
iar coeficientul de pe langa x2 este pozitiv
(a = 1)) si se obtine inecuatia
(aceasta expresie ia numai valori mai mari ca zero, oricare n-ar fi
x, deoarece discriminantul trinomului
1 - x + x2 este negativ
(D = 1 - 4 = -3 < 0)
iar coeficientul de pe langa x2 este pozitiv
(a = 1)) si se obtine inecuatia


![]() si deci |x + 1| = x + 1,
si deci |x + 1| = x + 1,
![]() este echivalenta cu sistemul
este echivalenta cu sistemul





![]() atunci
atunci
![]() de unde
de unde
![]() si inecuatia devine
si inecuatia devine
![]() rezulta
rezulta
![]() si prin urmare
si prin urmare
![]() Asadar
Asadar