Ecuatii irationale

Ecuatia ce contine necunoscuta sub semnul radicalului se numeste ecuatie irationala. Drept exemplu de ecuatii irationale pot servi

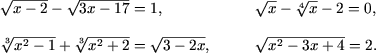
Mentionam, ca radacinile radicalului de ordin par ce figureaza in ecuatiile irationale se considera aritmetice, astfel valoarea radicalului de ordin par poate fi doar nenegativa si radicalul de ordin par exista daca si numai daca expresia de sub radical este nenegativa.

Exemplul 1. Sa se rezolve ecuatiile

Rezolvare. a) Se observa ca membrul din dreapta ecuatiei este negativ, pe cind cel din stinga, fiind un radical de ordinul doi, poate primi doar valori nenegative. Asadar ecuatia nu are solutii.

b) Cum suma a doua expresii, valorile carora sunt numere negative, este egal cu zero, rezulta ca ambele expresii concomitent sunt egale cu zero. Asadar, ecuatia este echivalenta cu sistemul de ecuatii

	x - 2 = 0,
	x + 2 = 0,

care este incompatibil. Prin urmare, ecuatia nu are solutii.

c) Domeniul valorilor admisibile (concis DVA) al ecuatiei se determina din sistemul (expresiile ce se contin sub semnul radicalului de ordinul doi urmeaza a fi nenegative)

	3 - x ł 0,
	x - 5 ł 0.

Evident sistemul nu are solutii, si, prin urmare, ecuatia enuntata la fel nu are solutie.

d) DVA al ecuatiei x = 4 se determina rezolvind sistemul

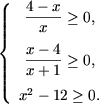
Cum x = 4 este unica valoare admisibila a ecuatiei, ramine de verificat, daca ea este sau ba solutie a ecuatiei. Introducind in ecuatie x = 4 se obtine egalitatea numerica justa 0 = 0 si, prin urmare, x = 4 este unica solutie a ecuatiei date.

e) DVA al ecuatiei x Î [2;4] se determina din sistemul de inecuatii

	x - 2 ł 0,
	x + 7 ł 0,
	4 - x ł 0.

Se observa ca in DVA are loc inegalitatea , si cum , rezulta ca ecuatia initiala nu are solutii.

f) Ecuatia se rezolva astfel

(4x² - 9)

= 0 Ű

		4x²-9 = 0,
		= 0,
		x ł 1,

		x = -³/₂,
		x = ³/₂,
		x = 1,
		x ł 1,

	x = ³/₂,
	x = 1.

Una din metodele standarde de rezolvare a ecuatiilor irationale consta in rationalizarea ei , adica in eliberarea succesiva de radicali pe calea ridicarii la o anumita putere a ambelor parti ale ecuatiei. Tinem sa mentionam (a se vedea [1]), ca daca n este un numar natural impar, ecuatiile f(x) = g(x) si (f(x))ⁿ = (g(x))ⁿ sunt echivalente, iar daca n este un numar natural par, ecuatia (f(x))ⁿ = (g(x))ⁿ este o consecinta a ecuatiei f(x) = g(x) (adica la ridicarea la putere para pot apare solutii straine), si, prin urmare, este necesara verificarea solutiilor obtinute.

Exemplul 2. Sa se rezolve ecuatiile

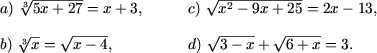
Rezolvare. a) Ambii membri ai ecuatiei se ridica la puterea a treia si se obtine ecuatia echivalenta

5x + 27 = x³ + 9x² + 27x + 27, sau x³ + 9x² + 22x = 0, de unde rezulta totalitatea

	x = 0,
	x² + 9x + 21 = 0.

Cum ultima ecuatie nu are solutii (D = 9² - 4·21 < 0), rezulta ca x = 0 este unica solutie a ecuatiei initiale.

b) Se ridica ambii membri ai ecuatiei la puterea a sasea (cel mai mic multiplu comun al ordinelor radicalilor (2 si 3) din ecuatie) si se obtine

x² = (x - 4)³ sau x³ - 13x² + 48x - 64 = 0, de unde, grupand convenabil, (x³ - 8x²) - (5x² - 40x) + (8x - 64) = 0, se obtine x²(x - 8) - 5x(x - 8) + 8(x - 8) = 0, sau (x - 8)(x² - 5x + 8) = 0. Astfel se obtine totalitatea

	x - 8 = 0,
	x² - 5x + 8 = 0,

cu solutia x = 8. Introducand x = 8 in ecuatia din enunt se obtine egalitatea numerica justa 2=2 si, prin urmare, x = 8 este solutie a ecuatiei enuntate.

c) Se ridica la patrat si se obtine ecuatia patrata

x² - 9x + 25 = 4x² - 52x + 169, sau 3x² - 43x + 144 = 0, cu solutiile x₁ = 9 si x₂ = ¹⁶/₃. Se efectueaza verificarea si ramane x = 9.

d) Se izoleaza un radical

si se ridica la patrat

iar se izoleaza un radical

si ridicand iar la patrat se obtine ecuatia 9(3 - x) = (3 - x)², cu solutiile x = 3 si x = -6. Prin verificare se constata ca atat x = 3 cat si x = -6 verifica ecuatia initiala.

Adesea este comoda si utila afirmatia (a se vedea [2]):

A1. Ecuatia este echivalenta cu sistemul

	f(x) = [g(x)]²ⁿ,
	g(x) ł 0.

Tinem sa mentionam ca conditia f(x) ł 0 este in aceasta situatie in plus, deoarece acei x₀ ce verifica ecuatia in conditiile sistemului, verifica si restrictia f(x₀) ł 0.

Nota. Din afirmatia A1 rezulta ca ecuatiile (b ł 0) si f(x) = [b]²ⁿ sunt echivalente.

Exemplul 3. Sa se rezolve ecuatiile

Rezolvare. a) Se utilizeaza afirmatia A1 (a se compara rezolvarea cu cea din exemplul 2d)) si se obtine sistemul

	x² - 9x + 25 = (2x - 13)²,
	2x - 13 ł 0,

echivalent cu

	3x² - 43x + 144 = 0,
	x ł ¹³/₂,

		x = ¹⁶/₃,
		x₂ = 9,
		x ł ¹³/₂,

de unde x = 9.

b) Se utilizeaza afirmatia A1 si se obtine

= x + 2

Ű	10 - x = (x + 2)²,
	x + 2 ł 0,

Ű	x² + 5x - 6 = 0,
	x ł -2,

Ű	x₁ = -6,	Ű x = 1.
	x₂ = 1,
	x ł -2,

Mentionam ca in procesul rezolvarii unei ecuatii irationale cu ajutorul DVA se tine seama de DVA pe tot parcursul rezolvarii ecuatiei.

Exemplul 4. Sa se rezolve ecuatiile

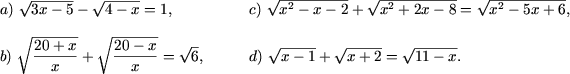
Rezolvare. a) DVA al ecuatiei este x Î [⁵/₃;4]. Ecuatia initiala este echivalenta cu ecuatia

. Cum ambii membri ai acestei ecuatii in DVA sunt nenegativi, ridicind la patrat se obtine ecuatia echivalenta

Utilizind afirmatia A1 si tinind seama de DVA se obtine

2x - 5 =

Ű	(2x - 5)² = 4 - x,
	x ł ⁵/₂,
	x Î [⁵/₃;4],

Ű	4x² - 19x + 21 = 0,	Ű
	x Î [⁵/₂;4],

Ű	x₁ = ⁷/₄,	Ű x = 3.
	x₂ = 3,
	x Î [⁵/₂;4],

b) DVA al ecuatiei este x Î (0;20]. Cum ambii membri sunt nenegativi, ridicand la patrat obtinem ecuatia echivalenta

sau, tinand seama ca x Î (0;20], si prin urmare

se obtine ecuatia

de unde

Ultima ecuatie in DVA este echivalenta cu sistemul

	(20 + x)(20 - x) = (3x - 20)²,
	3x - 20 ł 0,
	x Î (0;20]

echivalent cu

	10x² - 120x = 0,
	x Î [²⁰/₃;20]

		x₁ = 0,
		x₂ = 12,
		x Î [²⁰/₃;20]

de unde x = 12.

c) DVA al ecuatiei x Î (-Ą;-4]Č{2}Č[3,+Ą) se obtine rezolvand sistemul de ecuatii

	x² - x - 2 ł 0,
	x² + 2x - 8 ł 0,
	x² - 5x + 6 ł 0.

Se tine seama, ca daca AB ł 0, atunci si se obtine

de unde

Din prima ecuatie a totalitatii rezulta x = 2.

La rezolvarea ecuatiei ramase, se tine seama de DVA si se considera urmatoarele doua cazuri:

I. daca x Î (-Ą;-4], atunci ecuatia devine

Se ridica la patrat si se obtine ecuatia echivalenta

Se utilizeaza afirmatia A1 si se obtine

	4(1 + x)(x + 4) = (8 + x)²,
	x ł -8

sau, dupa transformari elementare

	3x² + 4x - 48 = 0,
	x ł -8

Se tine seama ca x Î [-8;-4] si se obtine solutia

II. daca x Î [3;+Ą) se obtine ecuatia

Cum x + 4 > x - 3, avem si tinind seama ca , rezulta ca ecuatia data nu are solutii pentru x ł 3.

Asadar solutiile ecuatiei din enunt sunt x = 2 si .

d) DVA al ecuatiei x Î [1;11] se determina rezolvand sistemul (conditiile de existenta a radicalilor de ordin par)

	x - 1 ł 0,
	x + 2 ł 0,
	11 - x ł 0.

Ambii membri ai ecuatiei sunt nenegativi si ridicand la patrat se obtine ecuatia echivalenta

care la randul sau este echivalenta cu sistemul (a se vedea afirmatia A1)

	4(x - 1)(x + 2) = (10 - 3x)²,
	10 - 3x ł 0,

	5x² - 64x + 108 = 0,
	x Ł ¹⁰/₃,

cu solutia x₁ = 2, ce verifica si DVA initial.

Ecuatiile de tipul

prin intermediul substitutiei

, se reduc la ecuatii algebrice.

Exemplul 5. Sa se rezolve ecuatiile

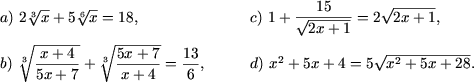
Rezolvare. a) Se noteaza (t ł 0), atunci si ecuatia devine

2t² + 5t - 18 = 0.

Rezolvand aceasta ecuatie patratica, se obtine t₁ = -⁹/₂ si t₂ = 2. Cum t ł 0 ramane t = 2 sau cu x = 2⁶ sau x = 64.

b) DVA al ecuatiei este R\{-4;-⁷/₅}. Se observa ca in ecuatie figureaza expresii reciproc inverse. Se noteaza , atunci si ecuatia devine

sau , dupa transformari elementare in DVA, 6t² - 13t + 6 = 0. Se rezolva ecuatia patratica si se obtine t₁ = ²/₃ si t₂ = ³/₂. Asadar

sau, ridicand la puterea a treia

de unde

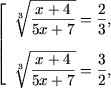
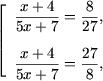
	x = 4,
	x = -¹⁵⁷/₁₂₇.

c) Se noteaza si ecuatia devine

sau 2t² - t - 15 = 0, de unde t₁ = -⁵/₂ (nu verifica conditia t > 0) si t = 3. Asadar

de unde tinand seama de nota la afirmatia A1 se obtine 2x + 1 = 9 si x = 4.

d) Se noteaza , atunci x² + 5x + 28 = t² sau x² + 5x = t² - 28 si ecuatia devine

t² - 28 + 4 = 5t sau t² - 5t - 24 = 0 cu solutiile t₁ = -3 si t₂ = 8.

Cum t ł 0 ramine t = 8 sau

Se ridica la patrat si se obtine ecuatia echivalenta

x² + 5x + 28 = 64, sau x² + 5x - 36 = 0 cu solutiile x = -9 si x = 4.

In unele cazuri ecuatia irationala se rationalizeaza, prin multiplicarea ambilor membri ai ecuatiei cu o expresie, ce nu primeste valoarea zero.

Exemplul 6. Sa se rezolve ecuatia

Rezolvare. Se multiplica ambii membri ai ecuatiei cu expresia

(conjugata expresiei din ecuatie) si, dupa reducerea termenilor asemenea, se obtine ecuatia

echivalenta cu cea enuntata, deoarece ecuatia

nu are solutii reale.

Adunand membru cu membru ecuatiile

se obtine ecuatia

Se ridica la patrat si se obtine ecuatia echivalenta (a se vedea nota la afirmatia A1)

3x² - x - 10 = 0 cu solutiile x₁ = -⁵/₃ si x₂ = 2.

Se efectueaza verificarea si se obtine ca atat x = -⁵/₃ cat si x = 2 sunt solutii ale ecuatiei enuntate.

Nota. Ecuatia data poate fi rezolvata si utilizind substitutia t = 3x² - x + 6, atunci 3x² - x-1 = 3x² - x + 6 - 7 = t - 7 si ecuatia devine

si se rezolva similar exemplului 2d).

Ecuatiile ce urmeaza se rezolva prin metoda evidentierii unui patrat complet sub semnul radicalului.

Exemplul 7. Sa se rezolve ecuatiile

Rezolvare. a) Se observa ca x² - 4x + 4 = (x - 2)², x² + 6x + 9 = (x + 3)², se tine seama ca si se obtine ecuatia

|x - 2| + |x + 3| = 5.

Cum |x - 2| = |2 - x|, (2 - x) + (x + 3) = 5 si astfel

|2 - x| + |x + 3| = |(2 - x) + (x + 3)| utilizand proprietatile modulului (a se vedea [1]) se obtine (2 - x)(x + 3) ł 0, de unde rezulta multimea solutiilor ecuatiei date: x Î [-3;2].

b) Se evidentiaza sub fiecare radical un patrat perfect

Se noteaza t ł 0 si ecuatia devine

|t - 2| + |t - 3| = t² echivalenta cu totalitatea

		0 Ł t Ł 2,
		-t + 2 - t + 3 = t²,
		2 < t Ł 3,
		t - 2 - t + 3 = t²,
		t > 3,
		t - 2 + t - 3 = t²,

		0 Ł t Ł 2,

		2 < t Ł 3,
		t = ±1,
		t > 3,
		t Î Ć,

de unde

. Asadar

In continuare se prezinta unele metode speciale de rezolvare a ecuatiilor irationale.

Exemplul 8. Sa se rezolve ecuatiile

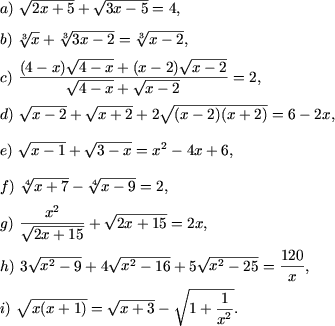
Rezolvare. a) Se verifica usor ca x = 2 este solutie a ecuatiei date. Alte solutii ecuatia nu are, deoarece membrul din stanga ca suma a doua functii strict crescatoare in [⁵/₃;+Ą), este o functie strict crescatoare, iar membrul din dreapta este o constanta, si, prin urmare, graficele acestor functii pot avea cel mult un punct de intersectie. Asadar x = 2 este unica solutie a ecuatiei.

b) Se ridica ambii membri ai ecuatiei la cub, utilizand formula (a + b)³ = a³ + b³ + 3ab(a + b)

(1)
sau, tinand seama ca (ecuatia enuntata),

(2)

Se ridica iar la cub si se obtine

x(3x - 2)(x - 2) = -x³ sau x[(3x - 2)(x - 2) + x²] = 0, de unde rezulta totalitatea de ecuatii

	x = 0,
	x² - 2x + 1 = 0,

	x = 0,
	x = 1.

Se efectueaza verificarea (este necesara deoarece ecuatiile (1) si (2) in general nu sunt echivalente) si se obtine unica solutie a ecuatiei enuntate x = 0.

c) DVA al ecuatiei este x Î [2;4]. Se noteaza , atunci

	4 - x = u²,
	x - 2 = v²,

de unde u² + v² = 2.

In u si v ecuatia devine

si cum u + v ą 0, rezulta u² - uv + v² = 2.

Rezolvand sistemul

	u² - uv + v² = 2,
	u² + v² = 2,

se obtine

	uv = 0,
	u² + v² = 2,

Deoarece u ł 0, v ł 0, ramane u₁ = 0,

v₂ = 0 de unde rezulta x₁ = 2 si x₂ = 4.

d) DVA al ecuatiei este x Î [2;3].

Se utilizeaza substitutia . Atunci sau si ecuatia devine

t + t² = 6, de unde t₁ = -3 (nu verifica conditia t > 0 ) si t = 2. Asadar

Se rezolva similar exemplului 8a) si se obtine x = 2.

e) DVA al ecuatiei este x Î [1;3]. Partea dreapta a ecuatiei se scrie x² - 4x + 6 = x² - 4x + 4 + 2 = (x - 2)² + 2 si in DVA primeste valoarea minima 2 pentru x = 2, iar partea din stanga ecuatiei obtine valoarea maxima 2 pentru x = 2 (se arata, de exemplu, cu ajutorul calculului diferential). Asadar, unica solutie a ecuatiei este x = 2.

f) Se noteaza u ł 0, v ł 0 si tinand seama de ecuatia din enunt, se obtine sistemul

	u⁴ - v⁴ = 16,
	u - v = 2,

care se rezolva in felul urmator: din a doua ecuatie a sistemului rezulta u = 2 + v, se inlocuieste in prima si se obtine ecuatia in v (2 + v)⁴ - v⁴ = 16, sau 16 + 32v + 24v² + 8v³ + v⁴ - v⁴ = 16, de unde rezulta totalitatea

	v = 0,
	v² + 3v + 4 = 0,

cu solutia v = 0. Atunci u = 2 si rezolvand sistemul

se obtine x = 9.

g) Se observa ca x = 0 nu verifica ecuatia data. Se impart ambii membri ai ecuatiei la x si se obtine ecuatia

Cum (rezulta din inegalitatea dintre media aritmetica si media geometrica) avem

de unde, utilizand afirmatia A1 se obtine sistemul

	2x + 15 = x²,
	x > 0,

cu solutia x = 5. Se efectueaza verificarea si se obtine ca x = 5 este solutia ecuatiei din enunt.

h) Cum membrul din stinga ecuatiei este pozitiv rezulta ca membrul din dreapta la fel este pozitiv, si astfel DVA al ecuatiei este x Î [5;+Ą). In DVA membrul din stanga reprezinta o functie strict crescatoare, iar cel din dreapta o functie strict descrescatoare, prin urmare ecuatia poate avea cel mult o radacina. Verificand cea mai mica valoare posibila x = 5 se convinge ca ambii membri ai ecuatiei primesc aceeasi valoare. Asadar x = 5 este unica solutie a ecuatiei.

i) DVA al ecuatiei x Î [-3;-1]Č(0;+Ą).

Ecuatia se scrie

se ridica la patrat si se obtine ecuatia echivalenta

Cum , iar , rezulta sistemul

cu solutiile x = ±1. Se efectueaza verificarea si ramane x = -1.

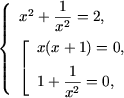
Exemple recapitulative