Inecuatii exponentiale

La rezolvarea inecuatiilor exponentiale se utilizeaza urmatoarele afirmatii (a se vedea, de exemplu, [2])

A.1. Daca a > 1, inecuatia

a^f(x) > a^g(x) este echivalenta cu inecuatia f(x) > g(x) adica semnul inecuatiei nu se schimba.

Similar a^f(x) < a^g(x) Ű f(x) < g(x).

A.2 . Daca 0 < a < 1, inecuatia

a^f(x) > a^g(x) este echivalenta cu inecuatia f(x) < g(x) adica semnul inecuatiei se schimba in opus.

Similar a^f(x) < a^g(x) Ű f(x) > g(x).

A.3. Inecuatia

[h(x)]^f(x) > [h(x)]^g(x) (1)

este echivalenta cu totalitatea de sisteme

		h(x) > 1,
		f(x) > g(x),
		0 < h(x) < 1,
		f(x) < g(x).

Nota. Daca semnul inecuatiei (1) nu este strict, se mai considera si cazul

	h(x) = 1,
	x Î D(f)Ç D(g),

unde D(f) (D(g)) desemneaza domeniul de definitie al functiei f (g).

A.4. Inecuatia

a^f(x) < b unde b Ł 0, nu are solutii (rezulta din proprietatile functiei exponentiale).

A.5. Inecuatia a^f(x) > b, unde b Ł 0 are solutiile x Î D(f)

A.6. Daca a > 1, inecuatia

a^f(x) > b unde b > 0, este echivalenta cu inecuatia f(x) > log_ab.

Similar a^f(x) < b Ű f(x) < log_ab.

A.7. Daca 0 < a < 1, inecuatia

a^f(x) > b unde b > 0, este echivalenta cu inecuatia f(x) < log_ab.

Similar a^f(x) < b Ű f(x) > log_ab.

Exemplul 1. Sa se rezolve inecuatiile:

a)	e) 2^x < -4,
b) (0.3)^\|2x-3\| < (0.3)^\|3x+4\|,	f) 2^x > -4,
c)	g)
d) (x²-x+1)^x Ł 1,	h)

Rezolvare. a) Cum 2 > 1, se utilizeaza afirmatia A.1 si se obtine inecuatia

care se rezolva prin metoda intervalelor (a se vedea [1],[2]), adica

b) Cum 0 < 0.3 < 1 se utilizeaza afirmatia A.2 si se obtine inecuatia

|2x-3| > |3x+4|, care se rezolva utilizand proprietatile modulului ([1],[2]), si anume |a| > |b| Ű (a-b)(a+b) > 0. Astfel |2x-3| > |3x+4| Ű ((2x-3)-(3x+4)) ((2x-3)+(3x+4)) > 0 Ű(-x-7)(5x+1) > 0

Ultima inecuatie se rezolva cu ajutorul metodei intervalelor si se obtine x Î (-7;-¹/₅).

c) Se utilizeaza afirmatia A.3 si se obtine

Ű		4x²+2x+1 > 1,
		x²-x > 0,
		4x²+2x+1 < 1,
		4x²+2x+1 > 0,
		x²-x < 0

Ű			x > 0,
			x < -¹₂,
			x > 1,
			x < 0,
			x Î (-¹₂;0),
			x Î R,
			x Î (0;1).

x Î (-Ą; -¹₂) Č(1;+Ą),

x Î Ć

Ű x Î (-Ą;- ¹₂) Č(1;+Ą).

d) Se tine seama de nota la afirmatia A.3 si se obtine

(x²-x+1)^x Ł 1Ű (x²-x+1)^x Ł (x²-x+1)⁰Ű

	x²-x+1 > 1,
	x Ł 0,
	x²-x+1 < 1,
	x²-x+1 > 0,
	x ł 0
	x Î D(f) ÇD(g) = R
	x²-x+1 = 1.

x < 0,

0 < x < 1,

x = 0, x = 1.

Ű x Î(-Ą;1].

e) Conform afirmatiei A.4 avem x Î Ć.

f) Se utilizeaza afirmatia A.5 si se obtine x Î R.

g) Utilizand afirmatia A.6 se obtine

x²-2x+3 < log₅7. Cum x²-2x+3 = x²-2x+1+2 = (x-1)²+2 ł 2, iar log₅7 < log₅25 = 2, rezulta ca aceasta inecuatie nu are solutii.

h) Multimea solutiilor inecuatiei se determina din sistemul (ce reprezinta DVA al inecuatiei):

	x-3 ł 0,
	x-8 ą 0,

Din ultimul sistem se obtine x Î [3;8)Č(8;+Ą).

Mentionam, ca toate procedeele de rezolvare a ecuatiilor exponentiale pot fi aplicate (cu modificarile respective) si in cazul inecuatiilor exponentiale.

Exemplul 2. Sa se rezolve inecuatiile

a) 5^2x+1 > 5^x+4,	d) 4^x²-x - 10·2^x² + 2^2x+4 ł 0,
b) 5·9^x - 18·15^x + 9·25^x > 0,	e)
c) 2^x+2 - 2^x+3 - 2^x+4 > 5^x+1 - 5^x+2,	f)

Rezolvare. a) Cum 5^2x+1 = 5·5^2x = 5·(5^x)², se noteaza t = 5^x si se obtine inecuatia patrata

5t²-t-4 > 0 cu solutiile t < -⁴/₅ sau t > 1. Cum t > 0 ramane t > 1, adica 5^x > 1, de unde x > 0.

b) Se observa ca inecuatia este omogena, se divide la 25^x si se obtine inecuatia

Se noteaza

si se rezolva inecuatia patrata 5t²-18t+9 > 0, obtinandu-se solutiile t < ³/₅ sau t > 3. Asadar

Se tine seama ca 0 < ³/₅ < 1 si se obtin solutiile x > 1 sau

. Asadar solutiile inecuatiei formeaza multimea

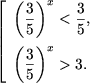
c) Se utilizeaza metoda factorului comun si se obtine

2^x+2 - 2^x+3 - 2^x+4 > 5^x+1 - 5^x+2 Ű 2^x·4 - 2^x·8 - 2^x·16 > 5^x·5 - 5^x·25 Ű Ű 2^x(4 - 8 - 16) > 5^x(5 - 25) Ű 2^x·(-20) > 5^x·(-20) Ű 2^x < 5^x Ű

d) Se divide inecuatia cu 2^2x si se obtine

se noteaza

si se rezolva inecuatia patrata t²-10t+16 ł 0, solutiile careia sunt t Ł 2 sau t ł 8. Asadar

de unde rezulta

	x²-2x Ł 1,
	x²-2x ł 3.

Solutiile primei inecuatii a totalitatii sunt , iar a inecuatiei secunde x Î (-Ą;-1]Č[3;+Ą).

Astfel .

e) Se noteaza t = 3^x si se utilizeaza metoda intervalelor (se tine seama ca t+5 > 0):

Astfel ¹/₃ < 3^x Ł 3 Ű 3^-1 < 3^x Ł 3¹ Ű x Î (-1;1].

f) Se grupeaza convenabil, si se obtine

Cum rezulta si astfel se obtine x-3 Ł 0, de unde x Ł 3. Se tine seama de DVA al inecuatiei: x ł 0 si se obtine raspunsul x Î [0;3].

In cele ce urmeaza se enunta cateva exemple de inecuatii exponentiale ce se rezolva prin metode speciale: tinand seama de domeniile de definitie si variatie, de monotonie, continuitate etc (a se vedea [2]).

Exemplul 3. Sa se rezolve inecuatiile:

a)	d)
b) 3^x+4^x ł 25,	e)
c)

Rezolvare. a) DVA a inecuatiei se determina rezolvand sistemul

	x-5 > 0,
	4-2^x-2 ł 0.

Se obtine

	x > 5,
	x Ł 4,

adica DVA a inecuatiei este o multime vida si, prin urmare, inecuatia data nu are solutii.

b) Membrul din stanga inecuatiei reprezinta o functie cresctoare (ca suma a doua functii crescatoare). Cum pentru x < 2 avem f(x) < f(2) = 25, iar pentru x ł 2 avem f(x) ł f(2) = 25, rezulta ca multimea solutiilor inecuatiei este multimea [2;+Ą).

c) Se observa ca expresia a^b-a^c pentru a > 1 este de acelasi semn cu expresia (b-c), si de semne contrare, daca 0 < a < 1, rezulta ca pentru x Î (0;1)Č(1;+Ą). expresiile a^b-a^c si (a-1)(b-c) sunt de acelasi semn.