Ecuatii exponentiale

Ecuatia ce contine variabila necunoscuta la exponetul puterii se numeste ecuatie exponentiala.

Cea mai simpla ecuatie exponentiala este de forma

a^x = b, (1)

unde a > 0, a š 1.

Afirmatia 1. Pentru b Ł 0 ecuatia (1) nu are solutii, iar pentru b > 0 ecuatia data are o solutie unica: x = log_ab.

Exemplul 1. Sa se rezolve ecuatiile

a) 2^x = -4, b) 2^x = 4, c) 2^x = 5.

Rezolvare. a) Cum membrul din stanga ecuatiei este pozitiv pentru orice x Î R (a se vedea proprietatile functiei exponentiale), iar membrul din dreapta este negativ, ecuatia nu are solutii.

b) Utilizand afirmatia 1 se obtine x = log₂4 , adica x = 2.

c) Similar exemplului precedent se obtine x = log₂5.

Nota. Din afirmatia 1 rezulta ca ecuatia exponentiala de tipul

a ^f(x) = b, (2)

unde a > 0, a š 1 si b > 0, este echivalenta cu ecuatia

f(x) = log_ab.

Exemplul 2. Sa se rezolve ecuatiile

Rezolvare. a) Se tine seama de nota la afirmatia 1 si se obtine ecuatia trigonometrica

Cum

, rezulta

, de unde

b) Cum log₃9 = 2, se obtine ecuatia

|x²-x| = 2. Utilizand proprietatile modulului (a se vedea, de exemplu, [1]) se obtine

|x²-x| = 2

x²-x = 2,

x²-x-2 = 0,

x = -1,

x²-x = -2,

x²-x+2 = 0,

x = 2.

c) Logaritmand in baza 5 (ambii membri sunt pozitivi) se obtine

(2+4+6+...+2x) = 45 sau 1+2+...+x = 45. Utilizind formula pentru suma primilor n termeni ai progresiei aritmetice se obtine

de unde rezulta ecuatia patrata x²+x-90 = 0 cu solutiile x₁ = -10 si x₂ = 9. Cum x Î N, ramane x = 9.

La rezolvarea ecuatiilor exponentiale se utilizeaza urmatoarea afirmatie de baza referitoare la echivalenta ecuatiilor (a se vedea, de exemplu, [2]).

Afirmatia 2. Daca a > 0 si a š 1, atunci ecuatiile

a^f(x) = a^g(x) (3)
si

f(x) = g(x) sunt echivalente.

Nota. Ecuatiile de tipul

a^f(x) = b^g(x) (a > 0, a š 1, b > 0) se pot scrie astfel

si se rezolva utilizind afirmatia 2.

Unele ecuatii exponentiale se reduc la ecuatiile de tipul (1)-(3) cu ajutorul egalitatilor:

E1) a^x· a^y = a^x+y, E2)

E3) (a^x) ^y = a^x·y, E4)

E5) a^x· b^x = (ab)^x.

Exemplul 3. Sa se rezolve ecuatiile

d) 3^2x-1 = 7^x+1.

Rezolvare. a) Se utilizeaza egalitatile E1-E3, afirmatia 2 si se obtine

Ű 3^{2x+1+2(x+2)-3x} = 3⁵ Ű 2x+1+2x+4-3x = 5 Ű x = 0.

b) Cum (ab š 0), rezulta si utilizand proprietatile E4, E3 si E1 se obtine

de unde, in baza afirmatiei 2, rezulta ecuatia patrata 2x²-x-15 = 0 cu solutiile x = 3 si x = -5/2.

c) Cum 4^3x+1 = 4¹·4^3x = 4·(4³)^x = 4·64^x, ecuatia devine

4·64^x ·25^x = 6400 sau 64^x·25^x = 1600. Utilizand proprietatea E5 si afirmatia 2 se obtine 1600^x = 1600, de unde x = 1.

d) Se tine seama de nota la afirmatia 2 si se obtine

de unde rezulta ecuatia liniara 2x-1 = xlog₃7+ log₃7 sau x(2-log₃7) = log₃7+1 cu solutia

Daca ecuatia exponentiala este de tipul

F(a^f(x)) = 0,

(4)

atunci prin intermediul substitutiei t = a^f(x), se obtine ecuatia F(t) = 0, care de regula se rezolva mai simplu. In cele mai frecvente cazuri se intalnesc ecuatiile de tipul

A·a^2f(x) +B·a^f(x) +C = 0,	(5)
A·a^f(x)+ C·a^-f(x)+ B = 0

(A, B si C Î R), care cu ajutorul substitutiei t = a^f(x) se reduc la ecuatia patrata At²+Bt+C = 0.

Exemplul 4. Sa se rezolve ecuatiile:

a) 2^x+3·2^x-4 = 76, b) 3^-x+9· 3^x+9^x+1+9^-x-1=8, c)

d) 2^1+x-2^3-x = 15, e)

Rezolvare. a) 2^x+3·2^x-4 = 76 Ű . Se noteaza t = 2^x, si se obtine ecuatia liniara

16t+3t = 76·16, de unde t = 64. Asadar 2^x = 64 si x = 6.

b) Ecuatia se scrie

Se noteaza t = 3^x (atunci 9^x = t²), si se obtine ecuatia algebrica

care se reduce (a se vedea [1]) prin substitutia

(atunci

) la ecuatia patrata

sau z²+9z-90 = 0, de unde z₁ = -15, z₂ = 6. Cum t > 0, z₁ = -15 nu verifica ecuatia si ramane

de unde 9t²-6t+1 = 0 cu solutia t = 1/3. Asadar 3^x = 1/3, de unde x = -1.

c) Se noteaza , atunci si se obtine ecuatia patrata

t²-t-2 = 0 cu solutiile t₁ = -1 si t₂ = 2. Cum t > 0 (mai exact, deoarece x² ł 0,

), ramane t = 2, adica

de unde x² = 1 si deci x = ą1.

d) Cum 2^1+x = 2·2^x, , se noteaza t = 2^x si ecuatia devine

Se multiplica ambii membri ai ecuatiei cu t (t > 0) si se obtine ecuatia patrata

2t²-15t-8 = 0 cu solutiile

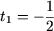si t₂ = 8. Cum t₁ < 0, ramane 2^x = 8, de unde x = 3.

e) Se noteaza (cum in x Î (-Ľ,0] Č[2,+Ľ), rezulta t ł 1) si se obtine ecuatia

4t²-9t+2 = 0 cu solutiile t₁ = 1/4 si t₂ = 2. Cum t₁ < 1 ramane de rezolvat ecuatia

echivalenta cu

Deoarece ambii membri ai ecuatiei sunt pozitivi, ridicand la patrat se obtine ecuatia echivalenta (a se vedea, de exemplu, [1])

x²-2x = 1 cu solutiile

Ecuatiile de tipul

A·a^2f(x) +B·a^f(x) b^f(x) +C·b^2f(x) = 0, (A, B, C Î R, A·B·C š 0) se numesc ecuatii exponentiale omogene. Prin multiplicarea, de exemplu, cu

ele se reduc la ecuatia patrata At²+Bt+C = 0, unde

Exemplul 5. Sa se rezolve ecuatiile

a) 64·9^x -84·12^x +27·16^x = 0, b) 9·2^2x+2 -45·6^x -3^2x+4 = 0.

Rezolvare. a) Ecuatia se scrie

64·3^2x -84·3^x ·4^x +27·4^2x = 0 si impartind la 4^2x se obtine

Se noteaza si se obtine ecuatia patrata

64t²-84t+27 = 0. Discriminantul ecuatiei date este D = 84² -4·64·27 = 4²· 3²·7² -4·4·16·9·3 = 4²·3²(49-48) = 12², iar solutiile

Asadar

de unde x₁ = 2 si x₂ = 1.

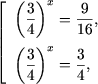
b) Ecuatia se scrie

36·2^2x -45·2^x· 3^x -81·3^2x = 0 sau (multiplicand cu

)

Notand se obtine ecuatia patrata

4t²-5t-9 = 0 cu solutiile t = -1, t = 9/4. Cum t > 0 ramane

de unde x = -2.

Uneori se intalnesc ecuatii ce se rezolva prin metoda "scoaterii factorului comun in afara parantezei".

Exemplul 6. Sa se rezolve ecuatiile

a) 2^x+1 - 2^x + 2^x-2 - 2^x-3 = 9,

b) 2^x+1 - 2^x+2 - 2^x+3 = 5^x - 5^x+1,

c) x²·2^x+1 + 2^|x-3|+2 = x²·2^|x-3|+4 + 2^x-1.

Rezolvare. a) Ecuatia se scrie

Efectuand operatiile din paranteze se obtine

de unde 2^x = 8 si x = 3.

b) Similar rezolvarii ecuatiei precedente se obtine:

2^x+1-2^x+2 -2^x+3 = 5^x-5^x+1 Ű 2^x·2-2^x·4 -2^x·8 = 5^x-5^x·5 Ű 2^x(2-4-8) = 5^x(1-5) Ű 2^x(-10) = 5^x(-4) Ű

c) Se trec toti termenii in partea stanga a ecuatiei si se grupeaza convenabil

(x²·2^x+1 -2^x-1)+(2^|x-3|+2- x²·2^|x-3|+4) = 0.

In fiecare paranteza se scoate factorul comun in afara parantezei

2^x-1(4x²-1) +2^|x-3|+2(1-4x²) = 0, de unde rezulta (4x²-1)·(2^x-1 -2^|x-3|+2) = 0 si totalitatea de ecuatii

	4x²-1 = 0,
	2^x-1 = 2^\|x-3\|+2.

Prima ecuatie are solutiile x₁ = -1/2, x₂ = 1/2, iar a doua se rezolva utilizand proprietatile modulului:

2^x-1 = 2^|x-3|+2 Ű x-1 = |x-3|+2 Ű x-3 = |x-3| Ű x-3 ł 0 Ű x ł 3. Asadar, solutiile acestei ecuatii sunt x Î {ą ¹/₂} Č[3,+Ľ).

Unele ecuatii exponentiale se rezolva prin metode specifice.

Exemplul 7. Sa se rezolve ecuatiile

a)	d) 4^x+(x-1)2^x = 6-2x,	g)
b) 5^x-2 = 8-x,	e) x²+x+2 = 2·2^x-4^x,	h)
c) 3^x+4^x = 5^x,	f)	i)

Rezolvare. a) Se observa ca si utilizand substitutia (atunci ) se obtine ecuatia

sau t²-62t+1 = 0 cu solutiile

. Cum

, se obtine totalitatea de ecuatii

de unde x₁ = 2 si x₂ = -2 ( se tine seama ca

b) Se observa ca x = 3 este solutie a ecuatiei date. Alte solutii ecuatia data nu are, deoarece membrul din stanga reprezinta o functie crescatoare, iar membrul din dreapta o functie descrescatoare, si cum graficele acestor functii pot avea cel mult un punct comun, rezulta ca x = 3 este unica solutie.

c) Se observa ca x = 2 este solutie a acestei ecuatii. Alte solutii ecuatia nu are. In adevar, ecuatia se scrie

Se observa ca functia

ca suma a doua functii descrescatoare este la fel descrescatoare si, prin urmare, capata fiecare valoare a sa doar o singura data.

d) Se noteaza t = 2^x si se rezolva ecuatia patrata in t:

t²+(x-1)t+2x-6 = 0.

Discriminantul acestei ecuatii este D = (x-1)²-4(2x-6) = x²-10x+25 = (x-5)², iar soluiile

Cum solutia t = -2 nu verifica conditia t > 0, ramane 2^x = 3-x Se rezolva similar exemplului b) si se obtine x = 1.

e) Ecuatia se scrie

x²+x+1 = 2·2^x-4^x-1 sau x²+x+1 = -(2^x-1)², de unde rezulta, ca ecuatia nu are solutii. In adevar, cum

membrul din stanga ecuatiei ia valori in multimea [³/₄; +Ľ), iar membrul din dreapta ecuatiei valori nepozitive.

f) Se observa ca ecuatia are solutii doar pentru x > 0. Atunci membrul din dreapta

in plus semnul egalitatii se obtine pentru x = 1 (se tine seama de inegalitatea

justa pentru orice a > 0), pe cand membrul din stanga ecuatiei primeste valoara maxima 2 pentru x = 1. In adevar

Astfel unica solutie a acestei ecuatii este x = 1.

g) Se observa, ca pentru x Î (-Ľ,-¹/₂] ecuatia nu are solutii (in adevar, in asa caz membrul din stanga ia valori nepozitive). Pentru x Î (-¹/₂;+Ľ) membrul din stanga reprezinta o functie strict crescatoare, ca produsul a doua functii strict crescatoare, si, prin urmare, primeste fiecare valoare a sa doar o singura data. Ramane de observat ca x = 0 este solutie (unica) a ecuatiei.

h) Domeniul valorilor admisibile al ecuatiei este multimea numerelor naturale, mai mari ca 1. Ecuatia se scrie

Se logaritmeaza, de exemplu, in baza 5 si se obtine

de unde se obtine ecuatia patrata x²+x(log₅2-3)-3log₅2 = 0 cu solutiile x₁ = 3 si x₂ = -log₅2. Cum x₂ Ď DVA, rezulta ca unica solutie a ecuatiei este x = 3.

i) DVA a ecuatiei este multimea x Î R\{ 0} si astfel (a se vedea exemplul precedent) solutiile ei sunt numerele 3 si -log₅2.

Uneori se intalnesc ecuatii ce contin necunoscuta atat in baza cat si in exponentul puterii:

[h(x)]^f(x) = b ([h(x)]^f(x) = [h(x)]^g(x)). (6)

De regula, domeniul de definitie pentru functia [h(x)]^f(x) ([h(x)]^g(x)) se considera multimea tuturor valorilor x Î D(f) (x Î D(f)ÇD(g) ), unde D(f) desemneaza domeniul de definitie al functiei f (f si g), pentru care h(x) > 0. Astfel:

[h(x)]^f(x) = [h(x)]^g(x) Ű

f(x) = g(x),

h(x) > 0,

h(x) š 1,

h(x) = 1,

x Î D(f) ÇD(g).

Exemplul 8. Sa se rezolve ecuatiile :

, c)

Rezolvare. a) Cum a² = |a|² ecuatia se scrie astfel

si este echivalenta cu totalitatea de sisteme

		\|x-2\| > 0,
		\|x-2\|š 1,
		x²+x+1 = 2,
		\|x-2\| = 1,
		x Î DVA.

de unde se obtin solutiile: x = -2, x = 3 si x = 1.

b) Se scrie (x²+x)⁰ = 1, si se obtine

		x²+x > 0,	Ű
		x²+x š 1,
		x²+2x = 0,
		x²+x = 1,

	x = -2,

c) DVA al ecuatiei este multimea (0;+Ľ). In DVA ecuatia este echivalenta cu totalitatea

		\|x-1\| > 0,
		\|x-1\| š 1,
		lg²x-lgx² = 3.
		\|x-1\| = 1,
		x > 0.

de unde rezulta solutiile x = ¹/₁₀, x = 1000 si x = 2.

Nota. Uneori este necesar ca functiile din (6) sa fie examinate pe domenii mai largi: se tine seama ca functia h(x)^f(x) are sens si atunci cand h(x) = 0 si f(x) > 0 (g(x) > 0) sau h(x) < 0 si f(x) (g(x)) ia valori in multmea numerelor intregi etc. (a se vedea [2]-[4]).

Exercitii de recapitulare