| Заглавная страница | Руководство пользователя | Практикум абитуриента | Учебные программы |
| Математический кружок | Занимательная математика| Формулы, словари | Новости |
|Странички истории | Экзамены, тесты | Библиография | Ссылки | Карта |

II. Тригонометрические неравенства

Основной способ решения тригонометрических неравенств состоит в их сведении к неравенствам вида
sinx Ъ a,     cosx Ъ a,     tgx Ъ a,     ctgx Ъ a, (1)
где a О R, символ "Ъ" означает знак сравнения и заменяет любой из знаков ">",   " ≥ ",   "<",  " ≤" и использовании следующих утверждений.

Утверждение 1. Множество решений неравенства
sinx > a (2)
есть

  1. R, если a < -1;
  2. (arcsina + 2pk; p - arcsina + 2pk), если -1 ≤ a < 1;
  3. Пустое множество, если a ≥ 1.

Утверждение 2. Множество решений неравенства
sinx < a (3)
есть

  1. R, если a > 1;
  2. (-p - arcsina + 2pk; arcsina + 2pk), если -1 < a ≤ 1;
  3. Пустое множество, если a ≤ -1.

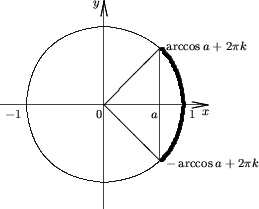
Утверждение 3. Множество решений неравенства
cosx > a (4)
есть

  1. R, если a < -1;
  2. (2pk - arccosa; 2pk + arccosa), если -1 ≤ a < 1;
  3. Пустое множество, если a ≥ 1.

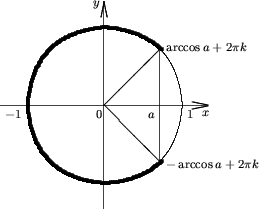
Утверждение 4. Множество решений неравенства
cosx < av (5)
есть

  1. R, если a > 1;
  2. (2pk + arccosa; 2p(k + 1) - arccosa), если -1 < a ≤ 1;
  3. Пустое множество, если a ≤ -1.

Утверждение 5. Множество решений неравенства
tgx > a (6)
есть

Утверждение 6. Множество решений неравенства
tgx < a (7)
есть

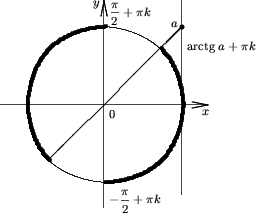
Утверждение 7. Множество решений неравенства
ctgx > a (8)
есть (pk; arcctga + pk).

Утверждение 8. Множество решений неравенства
ctgx < a (9)
есть (arcctga + pk; p(k + 1))

Замечания. 1. Если знак неравенства (2)-(9) нестрогий, то во множестве решений неравенства включается также и множество решений соответствующего уравнения.

2. Утверждения 1-8 легко доказать используя графики и свойства соответствующих тригонометрических функций.

Упражнение 1. Решить неравенства

1) 7) ctg2x - ctgx - 2 ≤ 0;
2) 8)
3) 9)
4) -2 ≤ tgx < 1; 10) 4sinxcosx(cos2x - sin2x) < sin6x;
5) 2sin2x - 5sinx + 2 > 0;         11) sinxsin3x ≥ sin5xsin7x;
6) 12) sinx + sin2x + sin3x > 0.

Решение. 1) Обозначив 2x = t, получим неравенство sint < 1/2 которое, согласно утверждению 2, имеет решения

Отсюда, учитывая что получим
или
или

Таким образом, множество решений исходного неравенства есть

2) Используя нечетность функции синус, получим

Обозначив , получим неравенство
решения которого (см. утверждение 1 и замечание 1) есть
Отсюда, учитывая что получим
или

3) Поскольку неравенство примет вид или Используя утверждение 3 получим

Так как следует
откуда

Данное неравенство можно решить и иначе.

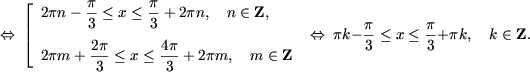
4) Используя утверждения 5 и 6, получим

-2 ≤ tgx < 1   Ы  
tgx < 1,
tgx ≥ -2,
   Ы  

5) Обозначим t = sinx и получим квадратное неравенство

2t2 - 5t + 2 > 0
решение которого есть
t < 1/2,
t > 2,
Отсюда следует совокупность неравенств
sinx > 2,
sinx < 1/2,
Первое неравенство совокупности решений не имеет, а из второго получим

6) Поскольку

sin4x + cos4x = (sin2x)2 + (cos2x)2 = (sin2x + cos2x)2 - 2sin2xcos2x =

неравенство примет вид
или Так как используя утверждение 3, получим
или

7) Положив t = ctgx, получим квадратное неравенство

t2 - t - 2 ≤ 0
решение которого -1 ≤ t ≤ 2, откуда -1 ≤ ctgx ≤ 2. Последнее неравенство решаем используя утверждения 7 и 8
-1 ≤ ctgx ≤ 2   Ы  
ctgx ≤ 2,
ctgx ≥ -1,
   Ы  
pk + arcctg2 ≤ x < p + pn,     n О Z
   Ы  

8) Используя метод вспомогательного угла, получим

9) Сделаем подстановку tgx = t и решим неравенство используя метод интервалов

Таким образом пролучена совокупность неравенств

0 < tgx ≤ 1,
tgx < -1,
которое решается используя утверждения 5 и 6
0 < tgx ≤ 1,
tgx < -1
   Ы  
tgx ≤ 1,
tgx > 0,
   Ы  

10) Используя формулы синуса и косинуса двойного аргумента получим

4sinxcosx(cos2x - sin2x) < sin10x   Ы   2sin2x·cos2x < sin6x   Ы

Ы   sin4x < sin6x   Ы   sin6x - sin4x > 0   Ы   2sinxcos5x > 0.

Учитывая что 2p есть один из периодов функции f(x) = sinxcos5x и используя обобщенный метод интервалов для интервала длины 2p, получим

Таким образом, множество решений данного неравенства есть обьединение множеств:

11) sinxsin3x ≥ sin2xsin4x   Ы   1/2(cos2x - cos4x) ≥ 1/2(cos2x - cos6x)   Ы   -cos4x ≥ -cos6x   Ы   cos6x - cos4x ≥ 0   Ы   -2sinxsin5x ≥ 0   Ы   sinxsin5x ≤ 0.

Решая последнее неравенство и аналогично предыдущему примеру получим

12) sinx + sin2x + sin3x > 0   Ы   (sinx + sin3x) + sin2x > 0   Ы   2sin2xcosx + sin2x > 0   Ы

Ы   sin2x(2cosx + 1) > 0   Ы  
sin2x > 0,
cosx > -1/2,
sin2x < 0,
cosx < -1/2,
  Ы

Упражнения для самостоятельного решения

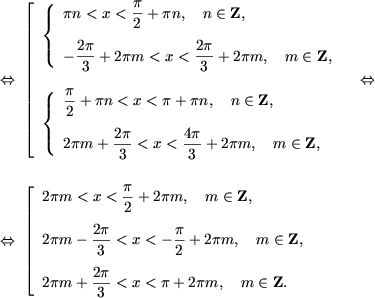
Решить неравенства

  1. tg3x + tg2x - tgx - 1 > 0.

  2. tgx + ctgx ≤ 2.

  3. sin2x < cosx.

  4. cosx + cos2x + cos3x ≥ 0.

  5. 6sin2x - 5sinx + 1 > 0.

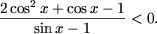
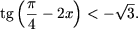
  9. 2sin2x + 9cosx - 6 ≥ 0.

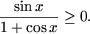
  12. cos2x + sinx ≥ 0.


| Заглавная страница | Руководство пользователя | Практикум абитуриента | Учебные программы |
| Математический кружок | Занимательная математика| Формулы, словари | Новости |
|Странички истории | Экзамены, тесты | Библиография | Ссылки | Карта |