Уравнения второго порядка
| ax2 + bx + c = 0, | (1) |
Числа a, b и c из (1) называются
коэффициентами квадратного уравнения, а число
D =
b2 - 4ac - дискриминантом квадратного уравнения.
Пример 1. Следующие уравнения являются квадратными уравнениями
| a) 6x2 + 5x + 1 = 0, | здесь a = 6, b = 5, c = 1 |
| и D = 52 - 4·6·1 = 1; | |
| b) 9x2 - 12x + 4 = 0, | здесь a = 9, b = -12, c = 4 |
| и D = (-12)2 - 4·9·4 = 0; | |
| c) x2 - x - 2 = 0, | здесь a = 1, b = -1, c = -2 |
| и D = (-1)2 - 4·1·(-2) = 9; | |
| d) |
здесь
|
|
и |
Уравнения второго порядка можно решать используя следующее утверждение
Утверждение 1. Если a) дискриминант уравнения (1) положителен, то уравнение (1) имеет два различных действительных корня
|
|
(2) |
|
|
(3) |
Таким образом (см. пример 1),
- уравнение a) имеет два различных корня
x1 = -1/2 и
x2 = -1/3;
- уравнение b) имеет два равных корня
x1 = x2 = 2/3;
- уравнение c) имеет два различных корня x1 = -1 и
x2 = 2;
- уравнение d) не имеет действительных решений.
Уравнение второго порядка с a = 1 называется приведенным квадратным уравнением и обычно обозначается
| x2 + px + q = 0. | (4) |
|
|
(5) |
| x1 = x2 = - p/2, (D = 0). | (6) |
| ax2 + bx = 0, | (7) |
| ax2 + c = 0. | (8) |
|
|
|
|
Пример 2. Решить уравнения
Решение. a)
|
|
b) 9x2 - 25 = 0 Ы 9x2 = 25 Ы x2 = 25/9 Ы x1,2 = ±5/3;
c) ![]() откуда следует
что уравнение не имеет действительных корней (левая часть уравнения -
неотрицательна, а правая - отрицательное число).
откуда следует
что уравнение не имеет действительных корней (левая часть уравнения -
неотрицательна, а правая - отрицательное число).
В дальнейшем рассмотрим несколько типов уравнений которые сводятся к уравнениям второго порядка.
| ax4 + bx2 + c = 0 | (9) |
Пример 3. Решить уравнения
Решение. a) Обозначив x2 = t, (тогда x4 = t2) получим квадратное уравнение относительно t:
| x2 = 4, | |
| x2 = 25, |
b) Аналогично предыдущему примеру, получим квадратное уравнение
t2 + t - 6 = 0 решения которого t = -3 и
t = 2. Поскольку t = x2 і 0, остается t = 2 или x2 = 2,
откуда ![]()
c) Положив t = x2, получим квадратное уравнение 2t2 - 3t + 4 = 0 которое не имеет действительных корней. Следовательно и исходное уравнение не имеет действительных корней.
| ax4 + bx3 + cx2 + bx + a = 0 | (10) |
Посредством подстановки ![]() , симметричные уравнения четвертого порядка сводятся к
уравнениям второго порядка. Действительно, так как x = 0 не является
корнем уравнения (10) (a ≠ 0), разделив на
x2 обе части уравнения, получим равносильное уравнение
, симметричные уравнения четвертого порядка сводятся к
уравнениям второго порядка. Действительно, так как x = 0 не является
корнем уравнения (10) (a ≠ 0), разделив на
x2 обе части уравнения, получим равносильное уравнение
Обозначив ![]() , тогда
|t| ≥ 2 и поскольку
, тогда
|t| ≥ 2 и поскольку ![]() уравнение примет вид
уравнение примет вид
Замечание. Уравнение ax4
![]() bx3 ± cx2
± bx + a = 0 сводится к
уравнению второго порядка используя подстановку
bx3 ± cx2
± bx + a = 0 сводится к
уравнению второго порядка используя подстановку
![]()
Пример 4. Решить уравнения
| a) x4 + 5x3 + 2x2 + 5x + 1 = 0, |
| b) 2x4 + 3x3 - 4x2 - 3x + 2 = 0. |
Решение. a) Данное уравнение есть уравнение вида (10) Поскольку x = 0 не является корнем, разделив обе части уравнения на x2 ≠ 0 и удобно групируя, получим равносильное уравнение
b) Аналогично предыдущему примеру получим уравнение

x4 = 1/2.
| ax4 + bx3 + cx2 + dx + e = 0, | (11) |
Уравнения 11 сводятся к уравнениям второго порядка
посредством подстоновки
![]()
Пример 5. Решить уравнение
Решение. Заметим что
![]() и следовательно данное уравнение есть возвратное уравнение четвертого порядка.
и следовательно данное уравнение есть возвратное уравнение четвертого порядка.
Так как x = 0 не является решением уравнения, разделим на x2 (не теряя при этом решений) получим равносильное уравнение
Обозначим ![]() тогда
тогда
![]()
![]() и уравнение примет вид
и уравнение примет вид

| x2 + 2x - 2 = 0, | |
| x2 - x - 2 = 0, |
Уравнения вида
| (x + a)4 + (x + b)4 = c | (12) |
используя подстановку
![]() сводятся к биквадратному уравнению относительно t.
сводятся к биквадратному уравнению относительно t.
Пример 6. Решить уравнение
Решение. Сделаем подстановку
![]() и получим следующее уравнение относительно t:
и получим следующее уравнение относительно t:
| (x + a)(x + b)(x + c)(x + d) = m | (13) |
| (x + a)(x + b) = x2 + (a + b)x + ab |
| (x + c)(x + d) = x2 + (c + d)x + cd = x2 + (a + b)x + cd |
Пример 7. Решить уравнение
Решение. Заметим, что -2 + 7 = 1 + 4 и удобно группируя, получим
| x2 + 5x - 14 = -19, | |
| x2 + 5x - 14 = 1, |
Пример 8. Решить уравнения

Решение. a) ОДЗ уравнения есть множество
![]() На ОДЗ
уравнение равносильно следующему
На ОДЗ
уравнение равносильно следующему
b) ОДЗ уравнения есть множество R\{2;3}. Приводя к общему знаменателю получим
c) ОДЗ уравнения есть множество R\{3;4;5;6}. Имеем
| 2x - 9 = 0, | |
| x2 - 9x + 19 = 0 |
d) ОДЗ уравнения есть множество R\{1;3;4;5}. Выделим целую часть каждой дроби.
Приведя к общему знаменателю, получим
| x = 0, | |
| x2 - 14x + 37 = 0, |
Уравнения вида
|
|
(14) |
Пример 9. Решить уравнение
Решение. ОДЗ уравнения есть множество ![]() Поскольку x = 0 не является решением
данного уравнения, перепишем уравнение в виде
Поскольку x = 0 не является решением
данного уравнения, перепишем уравнение в виде
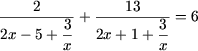
Обозначим ![]() и уравнение примет вид
и уравнение примет вид

|
или |
|
|
|
(15) |
Пример 10. Решить уравнения
Решение. a) ОДЗ уравнения есть множество
![]() Обозначим
Обозначим
![]() тогда
тогда
![]() и уравнение примет
вид
и уравнение примет
вид

b) ОДЗ уравнения есть множество R\{± 1}.
Заметив что x = ± 2 не являются решениями
данного уравнения, умножим обе части уравнения на выражение ![]() и получим равносильное
уравнение
и получим равносильное
уравнение
 |
или |
|
В некоторых случаях удобно выделить полный квадрат.
Пример 11. Решить уравнения
| a) x4 - 2x3 - x2 + 2x + 1 = 0; |
|
b) |
Решение. a) Выделим полный квадрат
| x4 - 2x2·x + x2 - x2 - x2 + 2x + 1 = 0, |
| (x2 - x)2 - 2(x2 - x) + 1 = 0. |
b) ОДЗ данного уравнения есть множество
![]() Прибавив к обеим частям уравнения выражение
Прибавив к обеим частям уравнения выражение
 |
или |
|
| ax2 + bx + c > 0, | (16) |
| ax2 + bx + c ≥ 0, | (17) |
| ax2 + bx + c < 0, | (18) |
| ax2 + bx + c ≤ 0, | (19) |
Квадратные неравенства решаются используя следующие утверждения.
Утверждение 2. Если a > 0 и дискриминант квадратного трехчлена ax2 + bx + x положителен, то
- неравенство (16) имеет решения x О (-Ґ;x1)И(x2;+Ґ);
- неравенство (17) имеет решения x О (Ґ;x1]И[x2;+Ґ);
- неравенство (18) имеет решения x О (x1,x2);
- неравенство (19) имеет решения x О [x1,x2]
где x1 и x2 (x1 < x2) есть корни трехчлена ax2 + bx + c.
Утверждение 3. Если a > 0 и дискриминант квадратного трехчлена ax2 + bx + c равен нулю, то
- неравенство (16) имеет решения x О R\{x1};
- неравенство (17) имеет решения x О R;
- неравенство (18) не имеет решений;
- неравенство (19) имеет единственное решение: x = x1,
где x1 есть двойной корень трехчлена ax2 + bx + c.
Утверждение 4. Если a > 0 и дискримининант трехчлена ax2 + bx + c отрицателен, то
Если a < 0, умножая неравенства (16)-(19) на (-1) (при этом знак неравенства меняется на противоположный) получим неравенства в котором a > 0 и применяем утверждения 2-4.
Пример 12. Решить неравенства
| a) x2 - x - 90 > 0; | d) x2 - x + 2 > 0; |
| b) 4x2 - 12x + 9 ≤ 0; | e) -6x2 + 5x - 1 ≤ 0; |
| c) x2 - 6x < 0; | f) 4x2 - x + 5 ≤ 0. |
Решение. a) Корни трехчлена x2 - x - 90 есть x1 = -9 и x2 = 10, a = 1 > 0, и, следовательно, множество решений неравенста x2 - x - 90 > 0 есть x О (-Ґ;-9)И(10;+Ґ).
b) Дискриминант трехчлена 4x2 - 12x + 9 равен нулю, a = 4 > 0 и следовательно, единственное решение неравенства 4x2 - 12x + 9 ≤ 0 есть x = 3/2.
c) Корнями трехчлена x2 - 6x являются x1 = 0 и x2 = 6, a = 1 > 0, следовательно x О (0;6) есть решения неравенства x2 - 6x < 0.
d) Дискриминант трехчлена x2 - x + 2 отрицателен, a = 1 > 0, и следовательно, любое действительное число удовлетворяет неравенство x2 - x + 2 > 0.
e) Умножим обе части неравенства на -1 и получим неравенство 6x2 - 5x + 1 ≥ 0. Используя утверждение 2, получим x О (-Ґ;1/3]И[1/2;+Ґ).
f) Неравенство не имеет решений.
При решении неравенств степени выше двух, можно использовать те же приемы, что и в случае уравнений (в некоторых случаях дополнительно используется и метод интервалов).
Пример 13. Решить неравенства
| a) 6x4 + 5x3 - 38x2 + 5x + 6 ≤ 0; |
| b) x(x - 2)(x - 4)(x - 6) ≥ 9; |
| c) x4 - 4x3 + 8x + 3 < 0; |
|
d) |
| e) 50x4 - 105x3 + 74x2 - 21x + 2 ≥ 0; |
|
f) |
| g) (x + 5)4 + (x + 3)4 < 272. |
Решение. a) Решив уравнение (см. (10))

Следовательно,
b) Используя метод решения уравнений вида (13) получим
|
|||||||||||||||||||
|
|||||||||||||||||||
|
|||||||||||||||||||
|
c) Выделяя полный квадрат, получим
| ||||||||||||||||
| ||||||||||||||||
|
d) Используя метод интервалов, получим
e) Решая уравнение (см. (11))

Следовательно
f) Так как x = 0 не является решением неравенства (0 > 1) исходное неравенство равносильно неравенству

Обозначив ![]() тогда
тогда
![]() неравенство
примет вид
неравенство
примет вид

Следовательно
 откуда
откуда
 или
или
|
Ы |
|
Ы x О (1;7). |
g) Сделаем подстановку ![]() t = x + 4 (см. (12))
тогда неравенство примет вид
t = x + 4 (см. (12))
тогда неравенство примет вид
Следовательно |x + 4| < 3. Используя свойства модуля получим
I. Решить уравнения
- x(x + 1)(x + 2)(x + 3) = 24.
- (1 - x)(2 - x)(x + 3)(x + 3) = 84.
- (x + 2)4 + x4 = 82.
- (2x2 + 5x - 4)2 -
5x2(2x2 + 5x - 4) +
6x4 = 0.
-
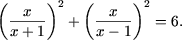
-

-
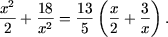
-

- x4 - 4x3 + 2x2 +
4x + 2 = 0.
- x4 + 6x3 + 5x2 -
12x + 3 = 0.
-
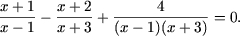
-

- (x2 + x + 1)(x2 + x + 2) = 12.
-

- 6x4 - 5x2 + 1 = 0.
II. Решить неравенства
-

- x4 - 8x3 + 14x2 +
8x - 15 ≤ 0.
-

-

-
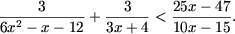
- x4 + x3 - 12x2 -
26x - 24 < 0.
-

- (x - 1)(x - 2)(x + 3)(x + 4)
≥ 84.
- (x - 1)4 + (x + 1)4
≥ 82.
-

Литература
- P.Cojuhari. Ecuatii si inecuatii. Teorie si practica.
Chisinau, Universitas, 1993.
- P.Cojuhari, A.Corlat. Ecuatii si inecuatii algebrice. Mica biblioteca a
elevului. Chisinau, Editura ASRM, 1995.
- Ф.Яремчук, П.Руденко. Алгебра и элементарные функции. Киев, Наукова Думка,
1987.
- Gh.Andrei si altii. Exercitii si probleme de algebra pentru concursuri si olimpiade scolare. Partea I, Constanta 1990.