Арифметические и геометрические прогрессии

Арифметическая прогрессия

Определение 1. Числовая последовательность (a_n)_{n
Î N} называется арифметической прогрессией, если существует действительное число d (называемое разностью прогрессии), такое, что
a_n+1 - a_n = d, ("n Î N) (1)

то есть, каждый член последовательности (начиная со второго) равен предыдущему плюс одно и то же число (разность прогрессии).

Пример 1. Проверить, являются ли данные последовательности арифметическими прогрессиями

a) a_n = 2n - 1, b) 3, 6, 9, ..., 3k, ... c) a_n = ¹/_n.

Решение. a) Разность a_n+1 - a_n является постоянным числом для любого n Î N

a_n+1 - a_n = 2(n + 1) - 1 - (2n - 1) = 2 следовательно, последовательность, заданная общим членом a_n = 2n - 1, является арифметической прогреcсией c разностью 2: 1, 3, 5, ..., 2n - 1, ...

b) Аналогично решению примера a), получим

a_n+1 - a_n = 3(n + 1) - 3n = 3, ("n Î N) и, следовательно, данная последовательность является арифметической прогрессией с разностью 3.

c) Выпишем первые три члена последовательности a₁ = 1, a₂ = ¹/₂, a₃ = ¹/₃ и заметим, что a₂ - a₁ = -¹/₂ ≠ a₃ - a₂ = -¹/₆, то есть, данная последовательность не образует арифметическую прогрессию.

Иначе, рассматривая разность , заметим, что она зависит от n (не является постоянным числом) и, следовательно, данная последовательность не является арифметической прогрессией.

Свойства арифметической прогрессии

Доказательства приведенных ниже свойств можно найти, например, в [1].

P1. Общий член арифметической прогрессии a_n определяется по формуле

a_n = a₁ + (n - 1)d, (2)

где a₁ - первый член прогрессии, d - ее разность.

P2. (Характеристическое свойство арифметической прогрессии). n-ый член арифметической прогрессии является средним арифметическим равноудаленных от него членов прогрессии:

a_n-k + a_n+k = 2·a_n, (3)

Замечание. Из свойства P2 следуют необходимые и достаточные условия:

a) три числа a, b, c (в указанной очередности) образуют арифметическую прогрессию, если

2b = a + b, (4)

b) три числа a, b, c (независимо от очередности) образуют арифметическую прогрессию, если

(2b - a - c)(2c - a - b)(2a - b - c) = 0. (5)

P3. Если a₁, a₂, ..., a_n, ... - арифметическая прогрессия и k + n = m + p (k,n,m,p Î N), то

a_k + a_n = a_m + a_p. (6)

P4. Сумма S_n первых n членов арифметической прогрессии равна

(7)

или, учитывая (2)

(8)

Определение 2. Арифметическая прогрессия называется возрастающей (убывающей если ее разность - положительное (отрицательное) число. Если разность прогрессии равна нулю, имеем постоянную последовательность.

Рассмотрим несколько примеров.

Пример 2. Определить арифметическую прогрессию, если a₃ = 2 и a₅ = -2.

Решение. Используя формулу общего члена арифметической прогрессии, получим систему

	a₃ = a₁ + 2d,
	a₅ = a₁ + 4d,

или, учитывая условия примера,

	a₁ + 2d = 2,
	a₁ + 4d = -2,

откуда находим первый член арифметической прогрессии a₁ = 6 и ее разность d = -2.

Пример 3. Определить число x, если числа a - x, x, b (a, b даны) в указанной последовательности образуют арифметическую прогрессию.

Решение. Используя характеристическое свойство арифметической прогрессии, получим линейное уравнение

2x = a - x + b, откуда

Пример 4. Определить арифметическую прогрессию, сумма первых n членов которой определяется по формуле

S_n = 3n² + 6n (n ≥ 1).

Решение. Поскольку сумма первых (n - 1) членов прогрессии равна

S_n-1 = 3(n - 1)² + 6(n - 1) = 3n² - 3, (n ≥ 2) и S_n - S_n-1 = a_n, следует, что a_n = 3n² + 6n - 3n² + 3 = 6n + 3.

Последовательно подставляя в формулу n-ого члена n = 1,2,3,..., получим a₁ = 9, a₂ = 15, a₃ = 21, ...

Пример 5. Определить сумму первых девятнадцати членов арифметической прогрессии a₁, a₂, a₃, ..., если

a₄ + a₈ + a₁₂ + a₁₆ = 224.

Решение. Заметим, что 4 + 16 = 8 + 12 и, следовательно, (см. (6)) a₄ + a₁₆ = a₈ + a₁₂. Учитывая, что сумма этих членов равна 224, найдем, что a₄ + a₁₆ = 112.

Поскольку (см. (7)) и a₁ + a₁₉ = a₄ + a₁₆ = 112 (1 + 19=4 + 16), то

Пример 6. При каких значениях параметра a существуют такие значения переменной x, чтобы числа

5^1+x + 5^1-x, ^a/₂, 25^x + 25^-x являлись последовательными членами арифметической прогрессии?

Решение. Согласно характеристическому свойству арифметической прогрессии, получим уравнение

a = 5^1+x + 5^1-x + 25^x + 25^-x.

Заметим, что при a ≤ 0 уравнение не имеет решений (правая часть, как сумма положительных чисел, есть положительное число).

Поскольку a^{x + y} = a^x·a^y, (a > 0, a ≠ 1), уравнение примет вид

Обозначим t ≥ 2 (сумма двух взаимно обратных положительных чисел). Тогда

и уравнение примет вид t² + 5t - (a + 2) = 0.

Положительный корень этого уравнения должен быть больше или равен 2 (данное уравнение имеет два различных противоположных по знаку корня, поскольку при a > 0 имеем -(a+2) < 0 и коэффициент при t² положителен), для чего достаточно, чтобы

	-^b/_2a < 2,
	f(2) ≤ 0,

или

	-⁵/₂ < 2,
	4 + 10 - (a + 2) ≤ 0,

откуда a ≥ 12.

Пример 7. Определить сумму всех четных трехзначных чисел, делящияся на 3.

Решение. Первым четным трехзначным числом, делящимся на 3, является 102. Поскольку четное число, делящееся на 3, делится и на 6, получим прогрессию

102, 108, 114, ..., 996, где a₁ = 102, d = 6 и последний ее член a_x = 996 (x Î N).

Поскольку a_x = a₁ + (x - 1)d или

102 + (x - 1)·6 = 996, находим x = 150. Тогда, используя формулу (7), получим

Пример 8. Пусть S_n, S_m и S_p - соответственно суммы первых n, m и p членов арифметической прогрессии a₁, a₂, a₃, ... Показать, что

(9)

Решение. Использем формулу (8), тогда равенство (9) примет вид

или 2a₁[m - p + p - n + n - m] + [(n - 1)(m - p) + (m - 1)(p - n) + (p - 1)(n - m)]d = 0.

Поскольку

(n - 1)(m - p) + (m - 1)(p - n) + (p - 1)(n - m) =

= nm - np - m + p + mp - mn - p + n + pn - pm - n + m = 0

получим: 2a₁·0 + 0·d = 0, то есть, 0 = 0, и, следовательно, равенство доказано.

Пример 9. Определить числа, являющиеся одновременно членами арифметической прогрессии, 2, 5, 8, ..., 332 и 7, 12, 17, ..., 157.

Решение. Пусть b - n-ый член первой прогрессии, следовательно, b = 2 + (n - 1)·3 и, в то же время, b является m-ым членом во второй прогрессии, то есть, b = 7 + (m - 1)·5. Таким образом, получим уравнение

2 + (n - 1)·3 = 7 + (m - 1)·5, или 3(n - 1) = 5m откуда, учитывая, что m, n - натуральные числа, получим n = 5k + 1 и m = 3k, k Î N, то есть, члены a₆, a₁₁, a₁₆, ..., a_5k+1 первой прогрессии совпадают с членами c₃, c₆, c₉, ..., c_3k, второй прогрессии. Таким образом, числа 17, 32, 47, 62, 77, 92, 107, 122, 137 и 152 входят в обе прогрессии.

Пример 10. Сумма трех положительных чисел равна ^p/₂. Найти произведение ctga· ctgg если известно, что ctga, ctgb, ctgg образуют арифметическую прогрессию.

Решение. Используя характеристическое свойство арифметической прогрессии, получим

2ctgb = ctga + ctgg. Поскольку a + b + g = ^p/₂ влечет b = ^p/₂ - (a + g), используя формулу приведения ctg(^p/₂ - x) = tgx получим 2tg(a + b) = ctga + ctgb, используя формулу тангенса двойного угла, имеем

откуда

Учитывая, что a, b и g - положительные числа, сумма которых равна ^p/₂ (tgatgg ≠ 1, tga ≠ 0, tgg ≠ 0), получим 2tgatgg = 1 - tgatgg откуда следует, что tgatgg = ¹/₃ и, следовательно, ctgactgg = 3.

Пример 11. Пусть x₁ и x₂ - корни уравнения x² + px + q = 0. Определить p и q, если известно, что q, x₁, p, x₂ (в данной очередности) образуют возрастающую арифметическую прогрессию.

Решение. Используя характеристическое свойство арифметической прогрессии и теорему Виета, получим систему

	2x₁ = q + p,
	2p = x₁ + x₂,
	x₁ + x₂ = -p,
	x₁x₂ = q,

решения которой

	q = -4,
	x₁ = -2,
	p = 0,
	x₂ = 2,

	q = 0,
	x₁ = 0,
	p = 0,
	x₂ = 0

По условию, арифметическая прогрессия - возрастающая и, следовательно, квадратное уравнение, удовлетворяющее условиям задачи, есть x² - 4 = 0 (p = 0, q = -4).

Пример 12. Определить первые три члена убывающей арифметической прогрессии, если известно, что a₁ + a₃ + a₅ = -24 и a₁a₃a₅ = 640.

Решение. Используя свойство P3, находим a₃ = -8, затем получим систему

	a₁ + a₅ = -16,
	a₁a₅ = -80,

решения которой a¢₁ = -20, a¢₅ = 4 и a¢¢₁ = 4, a¢¢₅ = -20. Поскольку прогрессия - убывающая (d < 0), остается a₁ = 4 и a₅ = -20. Используя свойство P3, получим

Таким образом, первыми тремя членами данной прогрессии являются 4, -2 и -8.

Геометрическая прогрессия

Определение 2. Числовая последовательность (b_n)_{n Î
N} называется геометрической прогрессией, если существует действительное число q, называемое знаменателем прогрессии, такое, что

b_n+1 = b_n·q, ("n Î N) то есть, каждый член последовательности (начиная со второго) равен предыдущему, умноженному на одно и то же число (знаменатель прогрессии).

Следующие последовательности являются геометрическими прогрессиями:

2, 4, 8, ..., 2ⁿ, ...	здесь b₁ = 2 и q = 2,
3, -1, ¹/₃, -¹/₃,...	здесь b₁ = 3 и q = -¹/₃,
a, a, a, ...	здесь b₁ = a и q = 1,
a, 0, 0, ...	здесь b₁ = a и q = 0

Заметим, что, если один из членов геометрической прогрессии равен нулю, то тогда либо b₁ = 0, либо q = 0.

Свойства геометрической прогрессии

P5. Формула n-го члена геометрической прогрессии:

b_n = b₁·q^n-1, ("n Î N). (11)

P6. (Характеристическое свойство геометрической прогрессии). Квадрат n-го члена геометрической прогрессии равен произведению равноудаленных от него членов:

(12)

В частном случае, для трех последовательных членов геометрической прогрессии

(13)

Замечание. Формулы (12), (13) можно записать и следующим образом:

(14)

(15)

то есть, модуль n-го члена геометрической прогрессии есть среднее геометрическое равноудаленных от него членов. В случае прогрессии с положительными членами n-ый член является средним геометрическим равноудаленных от него членов

(16)

P7. Если k + n = m + p (k, n, m, p Î N), тогда

b_k·b_n = b_m·b_p, (17)

где b_k, b_n, b_m, b_p - члены геометрической прогрессии b₁, b₂, ....

P8. Числа a, b, c (не обязательно в указанной очередности) образуют геометрическую прогрессию, если и только если удовлетворяют равенству

(a² - bc)(b² - ac)(c² - ab) = 0, (18)

а числа a, b, c (в указанной очередности) образуют геометрическую прогрессию, если и только если

b² = ac.

P9. Сумма S_n первых n членов геометрической прогрессии определяется по формуле

(19)

где b₁ - первый член прогрессии, q - её знаменатель, b_n - n-ый член прогрессии.

Если q = 1, то

S_n = b₁·n. (20)

P10. Сумма S всех членов бесконечно убывающей геометрической прогрессии (|q| < 1) определяется по формуле

(21)

Доказательства свойств P5-P10 можно найти, например, в [1].

Рассмотрим несколько примеров.

Пример 13. Произведение первых трех членов геометрической прогрессии равно 1728, а их сумма равна 63. Найти первый член и знаменатель этой прогрессии.

Решение. Пусть b₁, b₂ и b₃- первые три члена данной прогрессии. Тогда из условия b₁b₂b₃ = 1728 следует (см. (12 )) и b₂ = 12. Следовательно,

	b₁b₃ = 144,
	b₁ + b₃ = 51,

Решения данной системы (см. обратную теорему Виета) является также корнями квадратного уравнения z² - 51z + 144 = 0. Решая квадратное уравнение, получим z₁ = 3 и z₂ = 48, то есть, b₁ = 3, b₃ = 48 или b₁ = 48, b₃ = 3. Поскольку b₁ = 3, b₂ = 12 или b₁ = 48 и b₂ = 12, получим q = 4 или q = ¹/₄. Таким образом, решеними задачи будут b₁ = 3 и q = 4 или b₁ = 48 и q = ¹/₄.

Пример 14. В геометрической прогрессии с положительными членами (m + n)-ый член равен p, а (m - n)-ый член (m > n) равен s. Найти члены порядка m и n.

Решение. Поскольку (см. (11))

то

, и, поскольку b_m > 0, получим

Согласно условиям и формуле (10), получим

	b₁q^m+n-1 = p,
	b₁q^m-n-1 = s,

откуда

и, следовательно,

Поскольку b₁q^m+n-1 = b₁q^n-1·q^m = b_n·q^m = p, следует, что

Пример 15. Вычислить сумму

Решение. Имеем

или ⁹/₇·S_n = (10 - 1) + (100 - 1) + (10³ - 1) + ... + (10ⁿ - 1), откуда ⁹/₇·S_n = (10 + 10² + 10³ + ... + 10ⁿ) - n. Заметим, что в скобках - сумма первых n членов геометрической прогрессии с первым членом b₁ = 10 и знаменателем q = 10. Используя формулу (19), получим

, откуда

Пример 16. Доказать, что числа 9, 10 и 11 не могут являться членами одной геометрической прогрессии.

Решение. Пусть данные числа являются членами геометрической прогрессии с первым членом b₁ и знаменателем q. Тогда 9 = b₁q^k-1, 10 = b₁q^n-1 и 11 = b₁q^m-1, откуда следует

Таким образом,

, откуда

Поскольку m, n, k - различные натуральные числа, данное равенство ложно, и, следовательно, 9, 10 и 11 не могут быть членами одной геометрической прогрессии.

Пример 17. Числа a, b, c, d образуют геометрическую прогрессию. Показать, что (a - c)² + (b - c)² + (b - d)² = (a - d)².

Решение. Преобразуем левую часть равенства:

A = a² - 2ac + c² + b² - 2bc + c² + b² - 2bd + d². Так как b² = ac, c² = bd и bc = ad (см. (12) и (17)), то A = a² - 2b² + c² + b² - 2bc + c² + b² - 2c² + d² = a² - 2bc + d² = a² - 2ad + d² = (a - d)².

Пример 18. Сумма членов бесконечно убывающей геометрической прогрессии равна 4, а сумма их кубов равна 192. Найти пятый член последовательности.

Решение. Пусть b₁ и q - соответственно первый член и знаменатель данной геометрической прогрессии. Тогла |q| < 1 и

Заметим, что кубы членов исходной прогрессии образуют, в свою очередь, бесконечно убывающую геометрическую прогрессию с первым членом

и знаменателем q³. Действительно, поскольку

то

Следовательно,

Из первого уравнения находим b₁ = 4(1 - q) и подставляем во второе уравнение системы:

откуда (поскольку (|q| < 1) следует уравнение (1 - q)² = 3(1 + q + q²) или 2q² + 5q + 2 = 0 решения которого q₁ = -2 и q₂ = -¹/₂. Поскольку |q| < 1, остается q = -¹/₂ и, следовательно, b₁ = 6. Используя формулу n-го члена геометрической прогрессии, получим

Пример 19. Решить уравнения

Решение. Заметим, что числитель левой части уравнения представляет собой сумму бесконечно убывающей геометрической прогрессии с первым членом b₁ = 1 и знаменателем q₁ = tgx, а знаменатель левой части - сумму бесконечно убывающей геометрической прогрессии с первым членом 1 и знаменателем (-tgx). Поскольку |tgx| < 1, уравнение переписывается следующим образом:

или

Поскольку

уравнение примет вид

, откуда следует совокупность

или

Поскольку |tgx| < 1, остается x = pn, n Î Z.

Смешанные задачи

Пример 20. Определить числа a, b и c, если известно, что a, b, c - три последовательных члена геометрической прогрессии; a, b + 2, c образуют арифметическую прогрессию, а числа iar a, b + 2, c + 9 - геометрическую прогрессию.

Решения. Используя характеристические свойства геометрической и арифметической прогрессии, получим следующую систему:

	b² = ac,
	2(b + 2) = a + c,
	(b + c)² = a(c + 9),

откуда a = 4, b = 8, c = 16 или

Пример 21. Доказать, что если положительные числа a, b и c являются соответственно членами m, n и p-го порядка арифметической прогрессии a₁, a₂, ... и геометрической прогрессии b₁, b₂, ..., то a^b-c·b^c-a·c^a-b = 1.

Решение. Согласно условиям

a = a₁ + (m - 1)d,

b = a₁ + (n - 1)d,

c = a₁ + (p - 1)d,

(22)

где a₁ и d - соответственно первый член и разность арифметической прогрессии.

Из равенства (22) следует

b - c = (n - p)d, c - a = (p - m)d и a - b = (m - n)d. (23)

В то же время

a = b₁q^m-1, b = b₁q^n-1, c = b₁q^p-1, (24)

где b₁ и q - соответственно первый член и знаменатель геометрической прогрессии.

Используя (23) и (24), получим

Пример 22. Определить треугольник, длины сторон которого образуют геометрическую прогрессию, а величины внутренних углов - арифметическую прогрессию.

Решение. Пусть a, b, g - внутренние углы треугольника, противоположные сторонам a, b и c. Поскольку a + b + g = 180° и a = b - d, g = b + d, где d - разность арифметической прогрессии, получим

b - d + b + b + d = 180° откуда b = 60°.

Согласно теореме косинусов,

b² = a² + c² - 2accosb. Поскольку b² = ac и cosb = ¹/₂, то ac = a² + c² - ac откуда a² - 2ac + c² = 0 или (a - c)² = 0 и a = c.

Следовательно, получим равнобедренный треугольник (a = c) с углом при вершине в 60°, то есть, равносторонний треугольник.

Пример 23. Последовательность положительных чисел a₁, a₂, ..., a_n, ... образует арифметическую прогрессию, а последовательность b₁, b₂, ..., b_n, ... - геометрическую прогрессию. Доказать, что для любого натурального n, n > 2

a_n < b_n, если a₁ ≠ a₂, a₁ = b₁ и a₂ = b₂.

Решение. Пусть d - разность арифметической прогрессии, q - знаменатель геометрической прогрессии. Поскольку a₁ = b₁ и a₂ = b₂, получим

a₁ + d = a₁·q, откуда

и d = a₁(q - 1) > 0. Следовательно,

a_n = a₁ + (n - 1)d = a₁ + (n - 1)a₁(q - 1) = a₁(1 + (n - 1)(q - 1))

b_n = b₁q^n-1 = a₁q^n-1

и необходимо доказать неравенство a₁(1 + (n - 1)(q - 1)) < a₁q^n-1 или, так как a₁ > 0, 1 + (n - 1)(q - 1) < q^n-1. Последнее неравенство непосредственно следует из неравенства Бернулли (см. "Принцип математической индукции" или "Неравенства").

Другой способ. Рассмотрим разность

(было учтено, что

есть сумма первых n - 2 членов геометрической прогрессии с b¢₁ = 1 и q¢ = q).

Поскольку q > 1, q^k > 1, k Î N, получаем

1 + q + q² + ... + q^n-2 - (n - 1) > 0 а произведение (1 - q)(1 + q + q² + ... + q^n-2 - (n - 1)) < 0. Следовательно, и 1 + (n - 1)(q - 1) - q^n-1 < 0, то есть, a_n < b_n, n > 2.

Пример 24. Определить те прогрессии, которые одновременно является и арифметическими и геометрическими.

Решение. Пусть a₁, a₂, ..., a_n, ... - арифметическая и геометрическая прогрессия. Тогда 2a_k+2 = a_k+1 + a_k+3, или 2a₁q^k+1 = a₁q^k + a₁q^k+2, или a₁q^k - 2a₁q^k+1 + a₁q^k+2 = 0, откуда получим:

a₁q^k(1 - 2q + q²) = 0, a₁q^k(1 - q)² = 0.

Следовательно, если a₁q ≠ 0, то q = 1, и искомая прогрессия представляет собой постоянную последовательность a₁, a₁, ..., a₁, ... (d = 0, q = 1).

Если a = 0, получим 0, 0, ..., 0, ... (d = 0, q Î R), а если q = 0, a ≠ 0 - решений нет.

Упражнения

Пусть a₁, a₂, ..., a_n, ... - арифметическая прогрессия с положительными членами. Показать, что
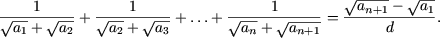
Показать, что где a₁, a₂, ..., a_n+1, ... - ненулевые члены арифметической прогрессии.
Определить трехзначные числа, делящиеся на 45, цифры которых образуют арифметическую прогрессию.
Решить уравнение 2 + 5 + 8 + 11 + ... + x = 155
Определить сумму всех двузначных четных чисел.
Найти a₁ + a₆ + a₁₁ + a₁₆, если a₁, a₂, ..., a_n, ... - арифметическая прогрессия и a₁ + a₄ + a₇ + ... + a₁₆ = 1447.
Определить те значения x, при которых число lg2, lg(2^x - 1), lg(2^x + 3) образуют арифметическую прогрессию.
Показать, что числа не могут быть членами одной арифметической прогрессии.
Пусть S_n, S_2n и S_3n - соответственно суммы первых n, 2n и 3n членов геометрической прогрессии. Доказать равенство S_n(S_3n - S_2n) = (S_2n - S_n)².
Определить четыре числа, образующих арифметическую прогрессию, сумма которых, равна 48, а отношение произведения крайних членов к произведению оставшихся равно
Определить геометрическую прогрессию, состоящую из семи членов, если известно, что сумма первых трех ее членов равна 26, а сумма последних трех равна 2106.
Доказать, что числа образуют геометрическую прогрессию.
Определить три числа, образующих геометрическую прогрессию, если их сумма равна 62, а сумма их квадратов равна 2604.
Числа a₁, a₂, a₃ образуют арифметическую прогрессию, а их квадраты - геометрическую прогрессию. Определить эти числа, если известно, что их сумма равна 21.
Определить арифметическую прогрессию, если сумма ее первых десяти членов равна 300, а первый, второй и пятый члены этой прогрессии образуют геометрическую прогрессию.

Литература

P.Cojuhari si altii. Progresii aritmetice si geometrice. Mica biblioteca a elevului. Seria Matematica, informatica. Chisinau, Editura ASRM, 1995.