Линейные уравнения и неравенства с параметром

Уравнение вида

ax + b = 0, (1)

где a,b О R, x - переменная, называется уравнением первой степени (линейным уравнением).

Ниже приведены примеры линейных уравнений:

a) 2x + 6 = 0,	где a = 2, b = 6;
b) x - 2 = 0	где a = 1, b = -2;
c) 0·x + 0 = 0,	где a = b = 0;
d) 0·x + ¹/₃ = 0,	где a = 0, b = ¹/₃;
e) -¹/₂x = 0,	где a = -¹/₂; b = 0.

Уравнение (1) равносильно уравнению

ax = -b откуда следует следующее утверждение.

Утверждение 1.

Если a ≠ 0, то уравнение (1) имеет единственное решение x = -^b/_a;
Если a = 0, b ≠ 0, то множество решений уравнения (1) пусто;
Если a = 0, b = 0, то любое действительное число является решением уравнения (1).

Таким образом, приведенные выше линейные уравнения решаются следующим образом:

a) x = -⁶/₂, то есть x = -3;
b) x = 2;
c) любое действительное число является решением данного уравнения;
d) уравнение не имеет решений;
e) x = 0.

Замечание 1. Уравнение

ax + b = cx + d, где a, b, c, d О R, сводится к линейному уравнению (1): ax + b = cx + d Ы (a - c)x + (b - d) = 0, или ax + b = cx + d Ы (a - c)x = d - b.

Замечание 2. Уравнение

(ax + b)(cx + d) = 0 где a, b, c, d О R, сводится к совокупности линейных уравнений

	ax + b = 0,
	cx + d = 0.

Пример 1. Решить уравнения

a) ,	c) -x + 2 = 2 - x,
b) 2x + 1 = 2x + 3,	d) (2x + 4)(3x - 1) = 0.

Решение. a) x = 6.

b) 2x + 1 = 2x + 3 Ы 2x - 2x = 3 - 1 Ы 0·x = 2 откуда следует, что уравнение не имеет решений.

c) -x + 2 = 2 - x Ы -x + x = 2 - 2 Ы 0·x = 0, следовательно, любое действительное число является решением уравнения.

d) (2x + 4)(3x - 1) = 0 Ы

2x + 4 = 0,

3x - 1 = 0,

Ы

x₁ = -2,

x₂ = ¹/₃.

В дальнейшем будут рассматриваться линейные уравнения с параметрами. Под параметром понимается (смотрите тему Уравнения с параметром) фиксированное (но неизвестное) число. Как правило, параметр обозначается первыми буквами латинского алфавита.

Пример 2. Решить уравнения

a) ax = 1;	e)
b) a²x - 1 = x + a;	f)
c) ax + b = cx + d;	g)
d) ;

Решение. a) Применяя утверждение 1, получим:

при a ≠ 0 уравнение имеет единственное решение, x = ¹/_a;

при a = 0 уравнение примет вид 0·x = 1 и, следовательно, оно не имеет решений.

Ответ: если a О R\{0}, то x = ¹/_a; если a = 0, то уравнение не имеет решений.

b) После элементарных преобразований получим:

a²x - 1 = x + a Ы a²x - x = a + 1 Ы x(a² - 1) = a + 1.

откуда, применяя утверждение 1, получим:

если a²-1 ≠ 0, то есть a ≠ ±1, то 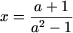или
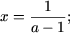
если a = 1, то уравнение примет вид 0·x = 2 и, следовательно, не имеет решений;
если a = -1, то уравнение примет вид 0·x = 0, и, следовательно, любое действительное число является решением этого уравнения.

c) Перепишем уравнение следующим образом

(a - c)x = d - b, откуда следует:

если a - c ≠ 0, то есть a ≠ c, то уравнение имеет единственное решение
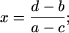
если a = c и d - b ≠ 0, то уравнение примет вид 0·x = d - b ( ≠ 0) и, следовательно, оно не имеет решений;
если a = c и d = b, то уравнение примет вид 0·x = 0, и, следовательно, множество его решений есть R

d) Область допустимых значений (ОДЗ) уравнения есть x ≠ 4. В ОДЗ уравнение решается следующим образом:

	x-2a = 0,
	x ≠ 4

	x = 2a,
	x ≠ 4.

Таким образом, если 2a ≠ 4, то есть a ≠ 2, то уравнение имеет единственное решение x = 2a, а если a = 2, то уравнение не имеет решений.

e) ОДЗ уравнения есть множество R\{-1;2}. Поскольку (x - a)(2x + a) = 0 влечет x₁ = a и x₂ = -^a/₂, так как x ≠ -1 и x ≠ 2, получим:

если a ≠ -1, a ≠ 2, -^a/₂ ≠ -1, -^a/₂ ≠ 2, то есть a О R\{-1;2;-4}, то уравнение имеет два решения x₁ = a и x₂ = -^a/₂ (если a = 0, решения совпадают);
если a = -1, то уравнение имеет единственное решение x = ¹/₂;
если a = 2, то уравнение не имеет решений;
если a = -4, то уравнение имеет единственное решение x = -4.

f) Если a = 0 или b = 0, то уравнение не имеет смысла. Пусть a·b ≠ 0. Тогда уравнение равносильно следующему

x(b + a) = abc откуда следует:

если b + a ≠ 0, то есть a ≠ -b, то уравнение имеет единственное решение
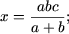
если a = -b и c ≠ 0, то уравнение не имеет решений.
если a = -b и c = 0, то любое действительное число есть решение данного уравнения.

g) ОДЗ уравнения определяется из системы

	5x -a ≠ 0,
	ax - 1 ≠ 0,

откуда x ≠ ^a/₅ и, если a ≠ 0, x ≠ ¹/_a. Если a = 0, то уравнение примет вид

или -2 = 15x,

откуда , и, поскольку следует, что если a = 0 то уравнение имеет решение .

Пусть a ≠ 0. Тогда в ОДЗ уравнение примет вид

2(ax - 1) = 3(5x - a), откуда (2a - 15)x = 2 - 3a и, следовательно,

если 2a - 15 ≠ 0, то есть то получим ;
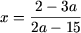если 2a-15 = 0, то есть то уравнение не имеет решений.

Таким образом для нужно проверить условие x ≠ ^a/₅ и x ≠ ¹/_a:

или (2a - 15)a ≠ 5(2 - 3a) откуда 2a² ≠ 10, или

Таким образом, для

уравнение не имеет решений.

В случае второго ограничения получим

или a(2 - 3a) ≠ (2a - 15), откуда 3a² = 15, то есть a² ≠ 5 (уже исследованный случай).

Таким образом, если уравнение не имеет решений, а если то уравнение имеет единственное решение

(заметим, что решение полученное в случае a = 0 содержится в приведенном выше результате).

Пример 3. Решить уравнения

a) \|x - a\| = 2;	c) \|x - a\| + \|x - 2a\| = a;
b) \|x\| + \|x - a\| = 0;	d) \|x - 1\| + \|x - 2\| = a.

Решение. a) Используя свойство модуля, получим:

|x - a| = 2 Ы

	x - a = 2,
	x - a = -2,

	x = a + 2,
	x = a - 2.

Таким образом, для любого действительного a уравнение имеет два различных решения, x₁ = a + 2 и x₂ = a - 2.

b) Левая часть уравнения принимает неотрицательные значения (как сумма двух неотрицательных слагаемых), а правая часть равна нулю. Следовательно,

	x = 0,
	x - a = 0,

или

	x = 0,
	x = a.

Таким образом, если a = 0, то система (а, следовательно, и уравнение) имеет единственное решение x = 0, а если a ≠ 0, то система (и исходное уравнение) решений не имеет.

c) Так как | f(x)| = |-f(x)| уравнение можно переписать следующим образом

|x - a| + |2a - x| = a.

Очевидно, что если a < 0, то уравнение не имеет решений, а если a=0, то получим |x| = 0, откуда x = 0.

Пусть a > 0. Тогда a = |a| = |(2a - x) + (x - a)|, и уравнение примет вид

|x - a| + |2a - x| = |(2a - x) + (x - a)|. Это уравнение равносильно (см. свойства модуля) неравенству (2a - x)(x - a) ≥ 0 откуда, учитывая, что 0 < a < 2a, получим решение x О [a;2a].

Таким образом:

если a < 0, то уравнение не имеет решений;

если a = 0, то уравнение имеет единственное решение x = 0;

если a > 0, то уравнение имеет бесконечное число решений - любое число

a ≤ x ≤ 2a.

d) Очевидно, что уравнение имеет решения только при a > 0. Рассмотрим три случая:

Пусть x < 1. Тогда |x - 1| = -(x - 1), |x - 2| = -(x - 2) и уравнение примет вид -x + 1 - x + 2 = a или -2x = a - 3 откуда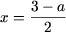 . Поскольку x < 1, то должно выполняться откуда a > 1. Таким образом, если a > 1, то ;
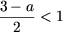
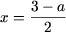Пусть x О [1;2]. Тогда |x - 1| = x - 1, |x - 2| = -(x-2) и уравнение примет вид x - 1 - x + 2 = a, 0·x = a - 1. Используя утверждение 1, получим:
если a = 1, то любое действительное число из отрезка [1;2] есть решение исходного уравнения;
если a ≠ 1, то решений нет.
Пусть x > 2. Тогда |x - 1| = x - 1, |x - 2| = x - 2 и уравнение примет вид x - 1 + x - 2 = a откуда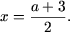 Поскольку x > 2, то 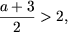то есть a > 1.
Таким образом:
если a > 1, то уравнение имеет два различных решения
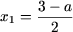и
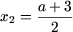
если a = 1, то любое число отрезка [1;2] есть решение уравнения;
если a < 1, то уравнение не имеет решений.

Линейные неравенства

Неравенства вида

ax + b > 0, ax + b ≥ 0, ax + b < 0, ax + b ≤ 0, (2)

где a, b О R, x - переменная, называются неравенствами первой степени (линейными неравенствами).

Поскольку все неравенства (2) решаются аналогично, приведем решение лишь первого из них: ax + b > 0. Рассмотрим следующие случаи:

a > 0, тогда ax + b > 0 Ы ax > -b Ы x > -^b/_a и, следовательно, множество решений неравенства ax + b > 0 (a > 0) есть (-^b/_a;+Ґ);
a < 0, тогда ax + b > 0 Ы ax > -b Ы x < -^b/_a и, следовательно, множество решений неравенства ax + b > 0 (a < 0) есть (-Ґ;-^b/_a);
a = 0, тогда неравенство примет вид 0·x + b > 0 и для b > 0 любое действительное число есть решение неравенства, а при b ≤ 0 неравенство не имеет решений.

Рассмотрим несколько примеров.

Пример 1. Решить неравенства

a) 3x + 6 > 0;	c) 2(x + 1) + x < 3x + 1;
b) -2x + 3 ≥ 0;	d) 3x + 2 ≥ 3(x - 1) + 1.

Решение. a) 3x + 6 > 0 Ы 3x > -6 Ы x > -2, и, следовательно, множество решений исходного неравенства есть (-2;+Ґ).

b) -2x + 3 ≥ 0 Ы -2x ≥ -3 Ы x ≤ ³/₂, то есть множеством решений исходного неравенства является (-Ґ;³/₂].

c) После элементарных преобразований получим линейное неравенство

2(x + 1) + x < 3x + 1 Ы 2x + 2 + x < 3x + 1 Ы 0·x + 1 < 0. Так как 1 < 0 - ложное числовое неравенство, то исходное неравенство не имеет решений.

d) Решая аналогично примеру c), получим

3x + 2 ≥ 3(x - 1) + 1 Ы 3x + 2 ≥ 3x - 3 + 1 Ы 0·x + 4 ≥ 0, откуда следует, что любое действительное число является решением исходного неравенства.

Пример 2. Решить неравенства

a) ax ≤ 1;

b) |x - 2| > -(a - 1)²;

c) 3(4a - x) < 2ax + 3;

d) abx + b > ax + 3;

f) ax + b > cx + d;

Решение. a) В зависимости от знака a рассмотрим три случая:

если a > 0, то x ≤ ¹/_a;
если a < 0, то x ≥ ¹/_a;
если a = 0, то неравенство примет вид 0·x ≤ 1 и, следовательно, любое действительное число является решением исходного неравенства.

Таким образом, если a > 0, то x О (-Ґ;¹/_a], если a < 0, то x О [¹/_a;+Ґ), и если a = 0, то x О R.

b) Заметим, что |x - 2| ≥ 0 для любого действительного x и -(a-1)² ≤ 0 для любого значения параметра a. Следовательно, если a = 1, то любое x действительное число, отличное от 2, является решением неравенства, а если a ≠ 1, то любое действительное число является решением неравенства. Ответ: если a = 1, то x О R\{2}, а если a О R\{1}, то x О R.

c) После элементарных преобразований получим

3(4a - x) < 2ax + 3 Ы 12a - 3x < 2ax + 3 Ы 12a - 3 < 2ax + 3x Ы x(2a + 3) > 3(4a - 1).

Далее рассмотрим три случая:

если 2a + 3 > 0, то есть a > -³/₂, то
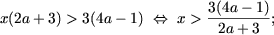
если 2a + 3 < 0, то есть a < -³/₂, то
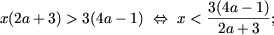
если 2a + 3 = 0, то есть a = -³/₂, то неравенство примет вид 0·x > -21 и, так как 0 > -21 - истинное числовое неравенство, следует, что любое действительное число является решением исходного неравенства.

Следовательно,

если то

если a = -³/₂, то x О R.

d) abx + b > ax + 3 Ы abx - ax > 3 - b Ы a(b - 1)·x > 3 - b.

Далее рассмотрим следующие случаи:

если a(b - 1) > 0, то есть a > 0 и b > 1, или a < 0 и b < 1, то
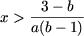
если a(b - 1) < 0, то есть a > 0 и b < 1, или a < 0 и b > 1, то
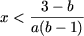
если a = 0, b ≠ 1 то неравенство примет вид 0·x > 3 - b и для b > 3 любое число является решением, а если b О (-Ґ;1)И(1;3], то множество решений неравенства пусто.
если a ≠ 0, b = 1, то неравенство примет вид 0·x > 2 и, очевидно, что оно решений не имеет.

Следовательно,

если a > 0 и b > 1, или a < 0 и b < 1, то

если a > 0 и b < 1, или a < 0 и b > 1, то

если a = 0 и b О (3;+Ґ), то x О R;

если a = 0 и b О (-Ґ;1)И(1;3) или a ≠ 0 и b = 1, то неравенство не имеет решений.

e) Заметим, что a ≠ ± 1, (в противном случае неравенство не имеет смысла). Неравенство переписывается следующим образом

Далее рассмотрим следующие случаи:

1. пусть a О (-Ґ;-1)И(1;+Ґ), тогда (a - 1)(a + 1) > 0 и, следовательно, исходное неравенство равносильно следующему

x(2 - 3a) + 3 - a ≤ 0, или x(2 - 3a) ≤ a - 3, откуда для a > 1

для a < -1

2. пусть a О (-1;1), тогда (a - 1)(a + 1) < 0, и, следовательно, исходное неравенство равносильно следующему

x(2 - 3a) + 3 - a ≥ 0 или x(2 - 3a) ≥ a - 3.

Последнее неравенство решается следующим образом:

если a = ²/₃, то x О R

если a О (-1;²/₃), то

если a О (²/₃,1), то .

Таким образом, исходное неравенство

при a О (-Ґ;-1)И(²/₃;1) имеет решения

при a О (-1;²/₃)И(1;+Ґ) имеет решения

при a = ²/₃, любое действительное число является решением исходного неравенства.

f) Исходное неравенство равносильно следующему

(a - c)x > d - b откуда следует, что

если a > c, то a - c > 0 и, следовательно,
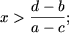
если a < c, то
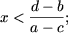
если a = c и d ≥ b, то множество решений неравенства пусто;
если a = c и d < b, то x О R.

g) Заметим, что a ≠ 0 и b ≠ 0. Приведя к общему знаменателю, получим

		2(b² - a²) - x(b - a)² > 0,
		ab > 0,
		2(b² - a²) - x(b - a)² < 0,
		ab < 0,

		x(b - a)² < 2(b² - a²),
		ab < 0,
		x(b - a)² > 2(b² - a²),
		ab < 0,


		ab > 0,
		a ≠ b,
		x О Ж,
		a = b,

		ab < 0.

Таким образом, если a и b одиннакогого знака (ab > 0) и a ≠ b, то множество решений неравенства есть если a и b - противоположных знаков (ab < 0), то множество решений есть este а если a = b то неравенство не имеет решений.

Пример 3. Решить неравенства

a) \|x + a\| + \|x - 2a\| < 4a;	c) \|x + a\| > 2;
b) \|x + a\| < \|a\|x;	d) \|x - a\| ≤ a.

Решение. a) Заметим, что при a ≤ 0 неравенство решений не имеет. Пусть a > 0. Рассмотрим три случая:

пусть x О (-Ґ;-a], тогда |x + a| = -x - a и |x - 2a| = 2a - x и неравенство примет вид -x - a + 2a - x < 4a, или x > -³/₂ a, поскольку a > 0, пересечением множеств (-Ґ;-a] и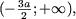 (а, следовательно, и множеством решений неравенства) явяется множество
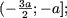
пусть x О (-a;2a], тогда |x + a| = x + a, и |x - 2a| = 2a - x, и неравенство примет вид x + a + 2a - x < 4a или 3a < 4a и, поскольку a > 0, любое число из интервала (-a;2a] есть решение неравенства;
пусть x О (2a;+Ґ), тогда |x + a| = x + a и |x - 2a| = x - 2a, и неравенство примет вид x + a + x - 2a < 4a или x < ⁵/₂ a. Учитывая условие x > 2a, получим x О (2a;⁵/₂a).

Таким образом, если a ≤ 0, то неравенство не имеет решений, а если a > 0, то множество решений неравенства есть (-³/₂a;-a]И(-a;2a]И(2a;⁵/₂a) или (-³/₂a;⁵/₂a).

b) Заметим, что неравенство может иметь лишь положительные решения. Для x > 0 неравенство переписывается |x + a| < |a|·|x| и решается, используя свойства модуля:

|x + a| < |a|·|x| Ы |x + a| < |ax| Ы (x + a + ax)(x + a - ax) < 0 Ы

Ы [(a + 1)x + a][(1 - a)x + a] < 0 Ы

		(a + 1)x + a > 0,
		(1 - a)x + a < 0,
		(a + 1)x + a < 0,
		(a + 1)x + a < 0,

		(a + 1)x > -a,
		(1 - a)x < -a,
		(a + 1)x < -a,
		(1 - a)x > -a.

Если a > 1, тогда a - 1 > 0 и a + 1 > 0, и первая система совокупности примет вид

откуда (учитывая, что x > 0) получим

а вторая система совокупности примет вид

и, так как a > 1 влечет

а x > 0, система не имеет решений.

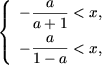
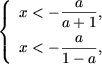
Если a = 1, то первая система совокупности не имеет решений, а из второй получим x < -¹/₂, и, так как x > 0, то и в этом случае исходное неравенство не имеет решений.

Если -1 < a < 1, то a + 1 > 0 и 1 - a > 0, и первая система совокупности примет вид

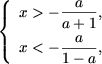или

откуда, заметив, что

получим, что первая система совокупности несовместна. Из второй системы получим

и, учитывая, что x > 0, получим

откуда a < 0. Таким образом, если a О [0;1), то неравенство не имеет решений, а если a О (-1;0), то множество решений неравенства есть

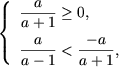
Если a = -1, то первая система совокупности несовместна, а из второй получим x > ¹/₂.

Если a < -1, то a + 1 < 0 и 1 - a > 0, и из первой системы следует

Так как a < -1 влечет

а x > 0, то в этом случае исходное неравенство не имеет решений. Вторая система совокупности примет вид

и, поскольку x > 0, получим

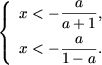
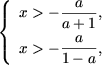
Таким образом,

если a О (-Ґ;-1)И(1;+Ґ), то

если a О [0;1], то неравенство не имеет решений;

если a = -1, то x О (¹/₂;+Ґ).

c) Используя свойство модуля, получим

|x + a| > 2 Ы

	x + a > 2,
	x + a < -2,

	x > 2 - a,
	x < -a - 2.

d) Если a < 0, то неравенство не имеет решений (левая часть неравенства неотрицательна). Если a = 0, то неравенство имеет единственное решение: x = 0. Если a > 0, то

|x - a| ≤ a Ы -a ≤ x - a ≤ a Ы 0 ≤ x ≤ 2a.