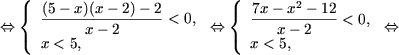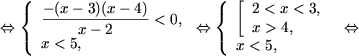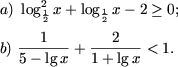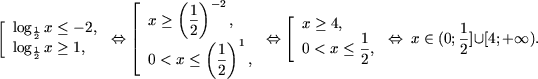Логарифмические уравнения
Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании,
называется логарифмическим уравнением.
Простейшим логарифмическим уравнением является уравнение вида
Утверждение 1. Если a > 0, a ≠ 1, уравнение (1) при
любом действительном b имеет единственное решение x =
ab.
Пример 1. Решить уравнения:
a) log2 x = 3,
b) log3 x = -1,
c) 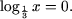
Решение. Используя утверждение 1, получим
a) x = 23 или x = 8;
b) x = 3-1 или x = 1/3;
c) 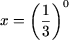 или x = 1. или x = 1.
Приведем основные свойства логарифма.
P1. Основное логарифмическое тождество:
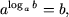 где a > 0, a ≠ 1 и b > 0.
где a > 0, a ≠ 1 и b > 0.
P2. Логарифм произведения положительных сомножителей равен сумме
логарифмов этих сомножителей:
loga N1·N2 =
loga N1 +
loga N2
(a > 0, a ≠ 1,
N1 > 0, N2 > 0).
Замечание. Если N1·N2 > 0,
тогда свойство P2 примет вид
loga N1·N2 =
loga |N1| +
loga |N2|
(a > 0, a ≠ 1,
N1·N2 > 0).
P3. Логарифм частного двух положительных чисел равен разности
логарифмов делимого и делителя
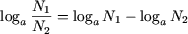 (a > 0, a ≠ 1, N1 > 0,
N2 > 0).
(a > 0, a ≠ 1, N1 > 0,
N2 > 0).
Замечание. Если 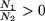 ,
(что равносильно N1N2 > 0)
тогда свойство P3 примет вид ,
(что равносильно N1N2 > 0)
тогда свойство P3 примет вид
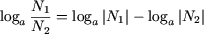 (a > 0, a ≠ 1,
N1N2 > 0).
(a > 0, a ≠ 1,
N1N2 > 0).
P4. Логарифм степени положительного числа равен произведению
показателя степени на логарифм этого числа:
loga N k =
k loga N
(a > 0, a ≠ 1, N > 0).
Замечание. Если k - четное число (k = 2s), то
loga N 2s =
2s loga |N|
(a > 0, a ≠ 1,
N ≠ 0).
P5. Формула перехода к другому основанию:
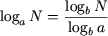 (a > 0, a ≠ 1,
b > 0, b ≠ 1, N > 0),
в частности, если N = b, получим
(a > 0, a ≠ 1,
b > 0, b ≠ 1, N > 0),
в частности, если N = b, получим
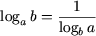
|
(a > 0, a ≠ 1,
b > 0, b ≠ 1).
|
|
(2) |
Используя свойства P4 и P5, легко получить
следующие свойства

|
(a > 0, a ≠ 1, b > 0,
c ≠ 0),
|
|
(3) |
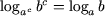
|
(a > 0, a ≠ 1, b > 0,
c ≠ 0),
|
|
(4) |
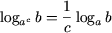
|
(a > 0, a ≠ 1, b > 0,
c ≠ 0),
|
|
(5) |
и, если в (5) c - четное число (c = 2n), имеет место
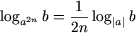
|
(b > 0, a ≠ 0,
|a| ≠ 1).
|
|
(6) |
Перечислим и основные свойства логарифмической функции
f(x) = loga x:
- Область определения логарифмической функции есть множество положительных
чисел.
- Область значений логарифмической функции - множество действительных чисел.
- При a > 1 логарифмическая функция строго возрастает
(0 < x1 < x2 Þ
loga x1 <
loga x2), а при 0 < a < 1,
- строго убывает (0 < x1 <
x2 Þ
loga x1 >
loga x2).
- loga 1 = 0 и loga a = 1
(a > 0, a ≠ 1).
- Если a > 1, то логарифмическая функция отрицательна при
x Î (0;1) и положительна при
x Î (1;+¥),
а если 0 < a < 1, то логарифмическая функция положительна при
x Î (0;1) и отрицательна при
x Î (1;+¥).
- Если a > 1, то логарифмическая функция выпукла вверх, а если
a Î (0;1) - выпукла вниз.
Следующие утверждения (см., например, [1]) используются
при решении логарифмических уравнений.
Утверждение 2. Уравнение loga f(x) =
loga g(x)
(a > 0, a ≠ 1) равносильно одной из систем (очевидно,
выбирается та система, неравенство которой решается проще)
 |
f(x) = g(x), |
|
 |
f(x) = g(x), |
| f(x) > 0, |
g(x) > 0. |
Утверждение 3. Уравнение logh(x) f(x) =
logh(x) g(x) равносильно одной из систем
 |
f(x) = g(x), |
|
 |
f(x) = g(x), |
| h(x) > 0, |
h(x) > 0, |
| h(x) ≠ 1, |
h(x) ≠ 1, |
| f(x) > 0, |
g(x) > 0. |
Нужно подчеркнуть, что в процессе решения логарифмических уравнений часто
используются преобразования, которые изменяют область допустимых значений
(ОДЗ) исходного уравнения. Следовательно, могут появиться "чужие"
решения или могут быть потеряны решения. Например, уравнения
f(x) = g(x) и
loga f(x) = loga g(x)
или
loga [f(x)·g(x)] = b
и
loga f(x) +
loga g(x) = b
вообще говоря, неравносильны (ОДЗ уравнений справа уже).
Следовательно, при решении логарифмических уравнений полезно использовать
равносильные преобразования. В противном случае, проверка полученных решений
является составной частью решения. Более того, необходимо учитывать и
преобразования, которые могут привести к потере корней.
Приведем основные способы решения логарифмических уранений.
I. Использование определения логарифма
Пример 2. Решить уравнения
| a) log2(5 + 3log2(x - 3)) = 3,
|
c) log(x - 2)9 = 2, |
b)  |
d) log2x + 1(2x2 - 8x + 15) = 2. |
Решение. a) Логарифмом положительного числа b по основанию a
(a > 0, a ≠ 1) называется степень, в которую нужно возвести число
a, чтобы получить b. Таким образом,
logab = c Û
b = ac и, следовательно,
5 + 3log2(x - 3) = 23
или
3log2(x - 3) = 8 - 5,
log2(x - 3) = 1.
Опять используя определение, получим
x - 3 = 21, x = 5.
Проверка полученного корня является неотъемлемой частью решения этого
уравнения:
log2(5 + 3log2(5 - 3)) =
log2(5 + 3log22) = log2(5 + 3) =
log28 = 3.
Получим истинное равенство 3 = 3 и, следовательно, x = 5 есть решение
исходного уравнения.
b) Аналогично примеру a), получим уравнение
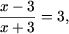 откуда следует линейное уравнение x - 3 = 3(x + 3) с решением
x = -6. Сделаем проверку и убедимся, что x = -6 является корнем
исходного уравнения.
откуда следует линейное уравнение x - 3 = 3(x + 3) с решением
x = -6. Сделаем проверку и убедимся, что x = -6 является корнем
исходного уравнения.
c) Аналогично примеру a), получим уравнение
(x - 2)2 = 9.
Возведя в квадрат, получим квадратное уравнение
x2 - 4x - 5 = 0 с решениями x1 = -1 и
x2 = 5. После проверки остается лишь x = 5.
d) Используя определение логарифма, получим уравнение
(2x2 - 8x + 15) = (2x + 1)2
или, после элементарных преобразований,
x2 + 6x-7 = 0,
откуда x1 = -7 и x2 = 1. После проверки
остается x = 1.
II. Использование свойств логарифма
Пример 3. Решить уравнения
| a) log3x + log3(x + 3) =
log3(x + 24), |
| b) log4(x2 - 4x + 1) -
log4(x2 - 6x + 5) =
-1/2 |
| c) log2x + log3x = 1, |
| d) 2log3(x - 2) +
log3(x - 4)2 = 0, |
| e) 16log4(1 - 2x) =
5x2 - 5. |
Решение. a) ОДЗ уравнения есть множество
x Î (0;+¥)
которое определяется из системы неравенств (условия существования логарифмов
уравнения)
 |
x > 0, |
| x+3 > 0, |
| x+24 > 0. |
Используя свойство P2 и утверждение
1, получим
|
log3x + log3(x + 3) =
log3(x + 24) Û
|
|
 |
log3x(x + 3) = log3(x + 24), |
| x > 0, |
|
Û
|
Û
 |
x(x + 3) = x + 24, |
| x > 0, |
|
Û
 |
x2 + 2x - 24 = 0, |
| x > 0, |
|
Û
 |
 |
x1 = -6, |
| x2 = 4, |
| x > 0, |
|
Û x = 4. |
b) Используя свойство P3, получим следствие исходного
уравнения
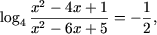 откуда, используя определение логарифма, получим
откуда, используя определение логарифма, получим
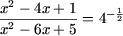 или
x2 - 4x + 1 =
1/2(x2 - 6x + 5),
откуда получаем уравнение
x2 - 2x - 3 = 0
с решениями x1 = -1 и x = 3. После проверки остается
лишь x = -1.
или
x2 - 4x + 1 =
1/2(x2 - 6x + 5),
откуда получаем уравнение
x2 - 2x - 3 = 0
с решениями x1 = -1 и x = 3. После проверки остается
лишь x = -1.
c) ОДЗ уравнения: x Î
(0;+¥). Используя свойство
P5, получим уравнение
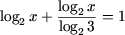
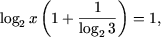 log2x(1 + log32) = 1,
откуда
log2x(1 + log32) = 1,
откуда 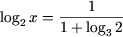 или
или 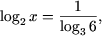 или log2x = log63.
Следовательно,
или log2x = log63.
Следовательно, 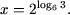
d) ОДЗ уравнения - множество
(2;4)È(4;+¥)
определяется из системы неравенств
 |
x-2 > 0, |
| (x - 4)2 ≠ 0, |
Используя свойство P4 (учитывая замечание), получим
равносильное уравнение
2log3(x - 2) + 2log3|x - 4| = 0
или log3(x - 2) + log3|x - 4| = 0.
Используя свойство P2, получим равносильное уравнение
log3(x - 2)|x - 4| = 0
(x - 2)|x - 4| = 1.
Поскольку в ОДЗ x - 2 = |x - 2| уравнение можно записать
следующим образом
|x - 2||x - 4| = 1 или
|x2 - 6x + 8| = 1
последнее уравнение (см. свойства модуля) равносильно совокупности уравнений
 |
x2 - 6x + 8 = 1, |
| x2 - 6x + 8 = -1, |
откуда получим: x1 = 3,
x2 = 3 +
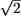 и x3 =
3 -
и x3 =
3 - 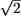 Ï ОДЗ. Таким образом, корнями исходного
уравнения являются x1 = 3 и
x2 = 3 +
Ï ОДЗ. Таким образом, корнями исходного
уравнения являются x1 = 3 и
x2 = 3 +
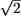 . .
e) Поскольку
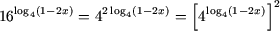 используя свойство P1, получим, что в ОДЗ
(x Î (-¥;-1))
уравнение равносильно уравнению
(1 - 2x)2 = 5x2 - 5
или
x2 + 4x - 6 = 0,
откуда следует: x1 = -2 -
используя свойство P1, получим, что в ОДЗ
(x Î (-¥;-1))
уравнение равносильно уравнению
(1 - 2x)2 = 5x2 - 5
или
x2 + 4x - 6 = 0,
откуда следует: x1 = -2 -
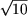 и x2 = -2 +
и x2 = -2 +
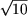 .
Последнее значение x не входит в ОДЗ, остается единственное
решение x = -2 - .
Последнее значение x не входит в ОДЗ, остается единственное
решение x = -2 -
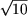 . .
III. Метод подстановки
В некоторых случаях логарифмическое уравнение можно свести к алгебрическому
уравнению относительно новой переменной. Например, уравнение
F(logax) = 0, где F(x)
- алгебраическая рациональная функция, посредством подстановки
logax = t сводится к алгебраическому уравнению
относительно t, R(t) = 0.
Пример 4. Решить уравнения
| a) lg2x - 3lgx + 2 = 0, |
c) lg2100x + lg210x + lgx = 14, |
b) 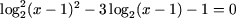 , , |
d) 5lgx = 50 - xlg5. |
Решение. a) ОДЗ уравнения есть множество
x Î (0;+¥).
Обозначив lgx = t (тогда
lg2x = (lg x)2 = t2),
получим квадратное уравнение
t2 - 3t + 2 = 0,
решения которого t1 = 1 и t2 = 2.
Следовательно,
 |
lg x = 1, |
| lg x = 2, |
откуда x1 = 10 и x2 = 100. Оба корня входят
в ОДЗ.
b) ОДЗ уравнения - множество (1;+¥).
Поскольку 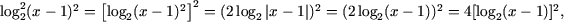 подстановкой t = log2(x - 1) получим квадратное
уравнение
подстановкой t = log2(x - 1) получим квадратное
уравнение
4t2 - 3t - 1 = 0
решениями которого являются t1 = -1/4 и
t2 = 1. Таким образом,
 |
log2(x - 1) = -1/4, |
| log2(x - 1) = 1, |
|
Û
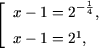
|
Û
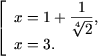
|
c) ОДЗ уравнения - множество (0;+¥). Так
как
lg2100x = (lg100x)2 =
(lg100 + lgx)2 = (2 + lgx)2,
lg210x = (lg10x)2 =
(lg10 + lgx)2 = (1 + lgx)2,
подстановкой t = lgx сведем исходное уравнение к квадратному
уравнению
(2 + t)2 + (1 + t)2 + t = 14
или
2t2 + 7t - 9 = 0
откуда t1 = -9/2 и
t2 = 1. Возвращаясь к исходной переменной, получим
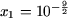 и
x2 = 10. и
x2 = 10.
d) ОДЗ уравнения - множество
(0;1)È(1;+¥). Поскольку
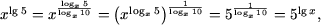 уравнение примет вид 5lg x = 50 - 5lg x или
2·5lg x = 50, откуда 5lg x = 25 или
5lg x = 52 Û
lgx = 2 Û x = 100.
уравнение примет вид 5lg x = 50 - 5lg x или
2·5lg x = 50, откуда 5lg x = 25 или
5lg x = 52 Û
lgx = 2 Û x = 100.
IV. Уравнения, содержащие выражения вида
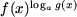
Пример 5. Решить уравнения
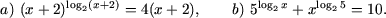
Решение. a) ОДЗ уравнения определяется из системы
 |
x + 2 > 0, |
| x + 2 ≠ 1. |
Получим множество x Î
(-2;-1)È(-1;+¥). В
ОДЗ обе части уравнения положительны, поэтому, логарифмируя обе части
уравнения (например, по основанию 2), получим равносильное уравнение
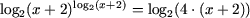 или, используя свойства P4 и
P2,
log2(x + 2)·log2(x + 2) =
log24 + log2(x + 2).
Обозначив log2(x + 2) = t, получим квадратное уравнение
t2 - t - 2 = 0
решениями которого являются t1 = -1 и
t2 = 2. Следовательно,
или, используя свойства P4 и
P2,
log2(x + 2)·log2(x + 2) =
log24 + log2(x + 2).
Обозначив log2(x + 2) = t, получим квадратное уравнение
t2 - t - 2 = 0
решениями которого являются t1 = -1 и
t2 = 2. Следовательно,
 |
log2(x + 2) = -1, |
| log2(x + 2) = 2, |
откуда
 |
x + 2 = 1/2, |
| x + 2 = 4 |
или
 |
x1 = -3/2, |
| x2 = 2. |
Оба корня входят в ОДЗ.
b) ОДЗ уравнения - множество
(0;1)È(1;+¥).
Поскольку (см. свойство proprietatea P5
и формулу (2))
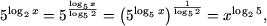
уравнение примет вид
 |
или |
 |
Логарифмируя обе части уравнения по основанию 2, получим
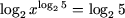 или log2x = 1, откуда x = 2.
или log2x = 1, откуда x = 2.
V. Некоторые специальные методы
Пример 6. Решить уравнения
|
a) 2x = 9 - log3x;
|
b) 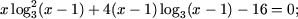
|
|
c) log2(x2 + 1) -
log2x = 2x - x2;
|
|
d) log5(x + 2) = 4 - x;
|
e) 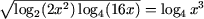
|
|
f) |log2(3x - 1) - log23| =
|log2(5 - 2x) - 1|;
|
|
g) logx+1(x3 -
9x + 8)logx-1(x + 1) = 3;
|
|
h) log2(6x - x2 - 5) =
x2 - 6x + 11.
|
Решение. a) Заметим, что x = 3 есть корень данного уравнения:
23 = 9-log33, 8 = 9-1, 8 = 8. Других решений уравнение не
имеет, так как левая часть уравнения представляет строго возрастающую функцию,
а правая часть - строго убывающую функцию. Графики таких функций имеют не более
одной точки пересечения и, следовательно, поскольку x = 3 является
решением, следует, что других решений нет.
b) ОДЗ уравнения есть множество x Î
(1;+¥). Обозначив
log3(x-1) = t получим квадратное уравнение
относительно t
xt2 + 4(x - 1)t - 16 = 0.
Дискриминант этого уравнения D =
[4(x - 1)]2 + 4x·16 =
16x2 + 32x + 16 = 16(x + 1)2, а
корни
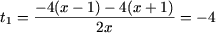 и
и
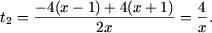 Таким образом, получена совокупность уравнений
Таким образом, получена совокупность уравнений

|
log3(x - 1) = -4,
|
|
log3(x - 1) = 4/x.
|
Из первого уравнения получим
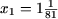 ,
а второе уравнение решается аналогично предыдущему примеру: заметив, что
x = 4 есть корень уравнения, доказывается, что других корней нет.
Следовательно, корнями исходного уравнения являются ,
а второе уравнение решается аналогично предыдущему примеру: заметив, что
x = 4 есть корень уравнения, доказывается, что других корней нет.
Следовательно, корнями исходного уравнения являются
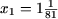 и x = 4. и x = 4.
c) ОДЗ уравнения определяется из системы

|
x2 + 1 > 0,
|
| x > 0, |
откуда следует x Î
(0;+¥). Используя свойство
P3, получим равносильное уравнение
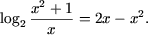
Поскольку 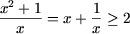 при x > 0, а знак равенства достигается лишь при x = 1,
то левая часть уравнения
при x > 0, а знак равенства достигается лишь при x = 1,
то левая часть уравнения
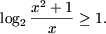 В то же время правая
часть уравнения принимает максимальное значение 1 при x = 1 (вершина
параболы y = 2x - x2 находится в точке
(1;1)). Следовательно, уравнение имеет решения только если В то же время правая
часть уравнения принимает максимальное значение 1 при x = 1 (вершина
параболы y = 2x - x2 находится в точке
(1;1)). Следовательно, уравнение имеет решения только если
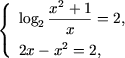 откуда x = 1. откуда x = 1.
d) Решая аналогично примеру a), получим x = 3.
e) Используя утверждение A1
(иррациональные уравнения), получим
f) Используя свойства P2, P3
и свойства модуля (см., например, [2]), получим
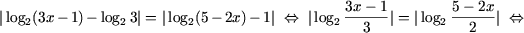
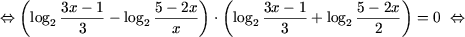
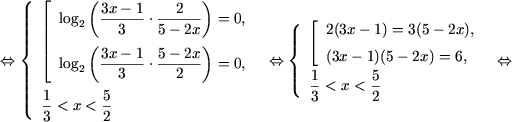
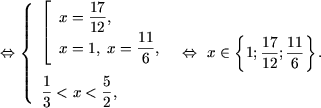
g) Находим ОДЗ уравнения
 |
x + 1 > 0, |
Û |
x > -1, |
| | Û |
| x + 1 ≠ 1, |
x ≠ 0, |
Û |
x > 1, |
| x3 - 9x + 8 > 0, |
x3 - x - 8x + 8 > 0, |
x ≠ 2, |
| x - 1 > 0, |
x > 1, |
(x - 1)(x2 + x - 8) > 0, |
| x - 1 ≠ 1, |
x ≠ 2, |
Û  |
x > 1, |
| x ≠ 2, |
| x2 + x - 8 > 0, |
|
Û  |
x > 1, |
| x ≠ 2, |
 |
|
Û
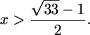
|
Используя свойство P5, получим (в ОДЗ)
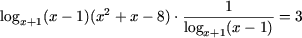 или
logx+1(x - 1)(x2 + x-8) =
logx+1(x - 1)3,
откуда следует уравнение
(x - 1)(x2 + x - 8) = (x - 1)3,
или
logx+1(x - 1)(x2 + x-8) =
logx+1(x - 1)3,
откуда следует уравнение
(x - 1)(x2 + x - 8) = (x - 1)3,
 |
x = 1, |
| x2 + x - 8 = x2 - 2x + 1, |
откуда x1 = 1, x2 = 3.
Поскольку x = 1 не удовлетворяет ОДЗ, а
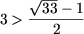 остается лишь x = 3.
остается лишь x = 3.
h) Поскольку функция f(x) = 6x - x2 - 5
достигает своего максимума 4 при x = 3, следует, что
log2(6x - x2 - 5) ≤ 2.
Правая часть уравнения x2 - 6x + 11 =
x2 - 6x + 9 + 2 = (x - 3)2 + 2 и,
следовательно, 2 - это наименьшее ее значение (достигается при x = 3).
Таким образом, уравнение имеет решение лишь в случае, если одновременно
log2(6x - x2 - 5) = 2 и
x2 - 6x + 11 = 2, то есть, если x = 3.
Логарифмические неравенства
Неравенство, содержащее неизвестное под знаком логарифма или (и) в его основании
называется логарифмическим неравенством.
В процессе решения логарифмических неравенств часто используются следующие
утверждения относительно равносильности неравенств и учитываются свойства
монотонности логарифмической функции.
Утверждение 1. Если a > 1, то неравенство
loga f(x) > loga g(x)
равносильно системе неравенств
 |
f(x) > g(x), |
| g(x) > 0. |
Утверждение 2. Если 0 < a < 1, то неравенство
loga f(x) > loga g(x)
равносильно системе неравенств
 |
f(x) < g(x), |
| f(x) > 0. |
Утверждение 3. Неравенство logh(x) f(x) >
logh(x) g(x)
равносильно совокупности систем неравенств
 |
 |
h(x) > 1, |
| f(x) > g(x) > 0, |
 |
0 < h(x) < 1, |
| 0 < f(x) < g(x). |
Подчеркнем, что в неравенстве loga f(x) >
loga g(x) вместо знака >
может фигурировать любой из знаков ≥ , < , ≤ .
В этом случае утверждения 1-3 соответственно
преобразуются.
Пример 1. Решить неравенства
| a) log3(x2 - x) ≥
log3(x + 8); |
d)  |
b) 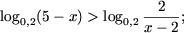
|
e) log2x(x2 - 5x + 6) < 1. |
c)  |
Решение. a) Используя утверждение 1 , получим
log3(x2 - x)
≥ log3(x + 8)
Û  |
x2 - x ≥ x + 8, |
Û  |
x2 - 2x - 8 ≥ 0, |
Û |
| x+8 > 0, |
x > -8, |
Û
 |
 |
x ≤ -2, | |
| x ≥ 4, |
Û x Î
(-8;-2]È[4;+¥). |
| x > -8, |
b) Основание логарифма число между нулем и единицей, поэтому, используя
утверждение 2, получим
c) Запишем 0 = log21 и, используя
утверждение 1, получим
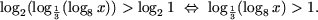
Запишем 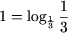 и, используя утверждение 2, получим
и, используя утверждение 2, получим
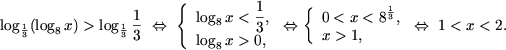
d) Используя утверждение 3, получим
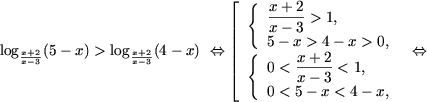
Û
 |
x Î (3;4), |
Û x Î (3;4).
|
| x Î Ж, |
Решение первой системы совокупности:
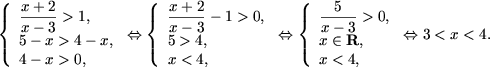
Решение второй системы совокупности:
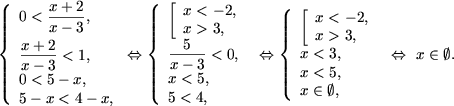
e) Запишем 1 = log2x2x, и используем
утверждение 3 (учитывая, что знак > заменен на знак
< ).
log2x(x2 - 5x + 6) <
log2x2x Û
 |
 |
2x > 1, |
|
| x2 - 5x + 6 < 2x, |
| x2 - 5x + 6 > 0, |
 |
0 < 2x < 1, |
| x2 - 5x + 6 > 2x, |
| 2x > 0, |
Û
 |
x Î (1;2)È(3;6), |
x Î
(0;1/2)È(1;2)È(3;6).
|
| x Î (0;1/2) |
Решение первой системы совокупности:
 | |
x > 1/2, |
Û
 | |
x > 1/2, |
Û x Î
(1;2)È(3;6). |
| x2 - 7x + 6 < 0, |
| 1 < x < 6, |
 |
x < 2, |
 |
x < 2, |
| x > 3, |
x > 3, |
Решение второй системы совокупности:
 |
0 < x < 1/2, |
| x2 - 7x + 6 > 0, |
|
Û
 | |
0 < x < 1/2, |
 |
x < 1, |
| x > 6, |
|
Û x Î
(0;1/2). |
Неравенства вида F(logax) > 0 сводятся
подстановкой t = logax к алгебраическому
неравенству F(t) > 0.
Пример 2. Решить неравенства
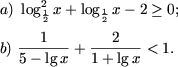
Решение. a) Обозначив
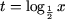 , получим
квадратное неравенство t2 + t - 2 ≥ 0, откуда
t ≤ -2 или t ≥ 1. Таким образом, , получим
квадратное неравенство t2 + t - 2 ≥ 0, откуда
t ≤ -2 или t ≥ 1. Таким образом,
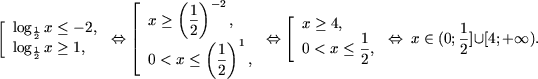
b) Обозначив t = lgx, получим рациональное неравенство
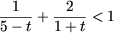 .
Используя метод интервалов (см., например,
[1], [2]), получим .
Используя метод интервалов (см., например,
[1], [2]), получим
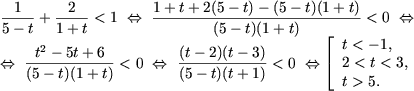
Следовательно,
 |
lgx < -1, |
|
 |
0 < x < 1/10, | |
| 2 < lgx < 3, |
Û |
100 < x < 1000, |
Û x Î
(0;1/10)È(100;1000)È(105;+¥). |
| lgx > 5, |
|
x > 105, |
В случае логарифмических неравенств, которые не имеют вид неравенств, входящих
в утверждения 1-3, определяется ОДЗ и с помощью
равносильных преобразований исходные неравенства сводятся к неравенствам,
которые решаются с помощью утверждений 1-3.
Пример 3. Решить неравенства
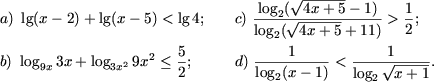
Решение. a) ОДЗ неравенства - множество
(5;+¥). Используя свойство
P2, получим неравенство
lg(x - 2)(x - 5) < lg4.
Используя утверждение 1, получим
 |
(x - 2)(x - 5) < 4, |
| (x - 2)(x - 5) > 0. |
Решаем систему
 | |
x2 - 7x + 6 < 0, | |
 | |
1 < x < 6, | |
 |
x < 2, |
Û |
 |
x < 2, |
Û x Î
(1;2)È(5;6) |
| x > 5, |
|
x > 5, |
и, учитывая ОДЗ, получим x Î (5;6).
e) Определим ОДЗ неравенства
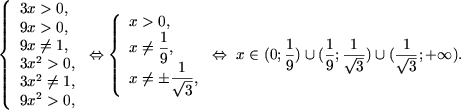 Приведя все логарифмы к основанию 3, получим
Приведя все логарифмы к основанию 3, получим
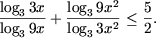 Используя свойство P2, получим
Используя свойство P2, получим
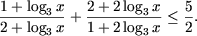 Обозначив log3x = t, решим полученное неравенство
методом интервалов
Обозначив log3x = t, решим полученное неравенство
методом интервалов
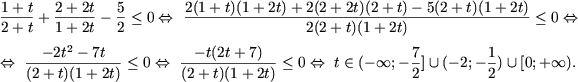
Следовательно,
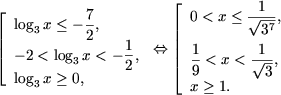 откуда, учитывая ОДЗ, получим множество решений исходного неравенства:
откуда, учитывая ОДЗ, получим множество решений исходного неравенства:
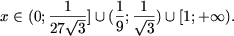
c) Определим ОДЗ неравенства
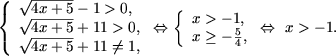
Поскольку
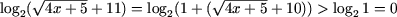 ,
неравенство равносильно следующему: ,
неравенство равносильно следующему:
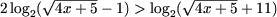 откуда следует
откуда следует
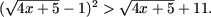 Обозначив
Обозначив 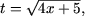 t ≥ 0, получим квадратное неравенство
(t - 1)2 > t + 11,
или
t2 - 3t - 10 > 0,
откуда t < -2 или t > 5. Поскольку t ≥ 0, остается
t > 5 или
t ≥ 0, получим квадратное неравенство
(t - 1)2 > t + 11,
или
t2 - 3t - 10 > 0,
откуда t < -2 или t > 5. Поскольку t ≥ 0, остается
t > 5 или 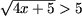 Û x > 5.
Û x > 5.
Учитывая ОДЗ, получим ответ: x Î
(5;+¥).
d) ОДЗ неравенства есть множество
(1;2)È(2;+¥).
Используя обобщенный метод интервалов, получим
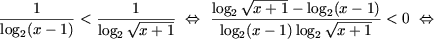
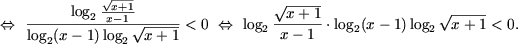
Так как в ОДЗ log2(x-1) > 0
при x > 2 и log2(x-1) < 0 при 1 < x < 2,
следует, что 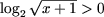 для любого x из ОДЗ,
для любого x из ОДЗ,
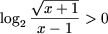 при x Î (1;2)È(2;3)
и
при x Î (1;2)È(2;3)
и 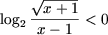 при x > 3, значит,
при x > 3, значит,
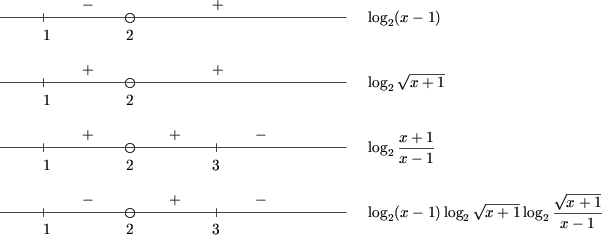
получим x Î
(1;2)È(3;+¥).
Для укрепления навыков решения логарифмических уравнений и неравенств
рекомендуем читателю, например, задачники [3-5].
Литература
- P. Cojuhari. Ecuatii si inecuatii. Teorie si practica.
Chisinau, Universitas, 1993.
- P. Cojuhari, A. Corlat. Ecuatii si inecuatii algebrice. Mica
biblioteca a elevului. Seria matematica si informatica. Editura
ASRM. Chisinau, 1995.
- C.Cosnita, F.Turtoiu. Probleme de algebra. Editura Tehnica. Bucuresti,
1989.
- Е.Д.Куланин и др. 3000 конкурсных задач по математике. Айрис Ролиф.
Москва, 1997.
- Ф.П.Яремчук, П.Рудченко. Алгебра и элементарные функции. Киев, Наукова
Думка. 1987.
| Заглавная страница |
Руководство пользователя |
Практикум абитуриента |
Учебные программы |
| Математический кружок |
Занимательная математика|
Формулы, словари |
Новости |
|Странички истории |
Экзамены, тесты |
Библиография |
Ссылки |
Карта |

|
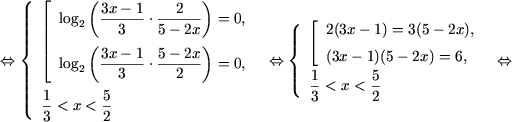
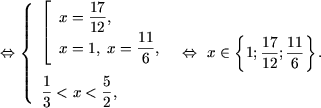
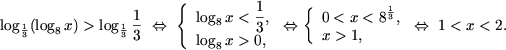
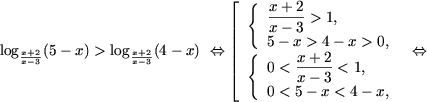
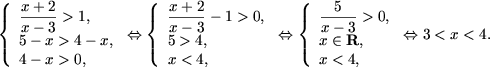
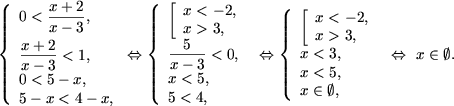
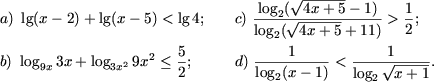
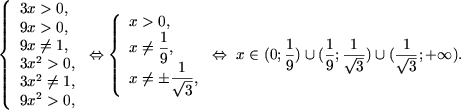
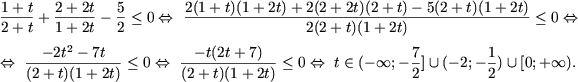
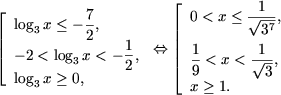
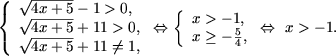
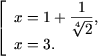
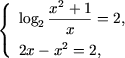 откуда x = 1.
откуда x = 1.

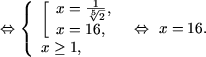

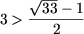 остается лишь x = 3.
остается лишь x = 3.