
| Заглавная страница |
Руководство пользователя |
Практикум абитуриента |
Учебные программы |
| Математический кружок |
Занимательная математика|
Формулы, словари |
Новости |
|Странички истории |
Экзамены, тесты |
Библиография |
Ссылки |
Карта |
Иррациональные неравенства
Неравенство, содержащее неизвестные величины или некоторые функциии неизвестных
величин под знаком радикала называется иррациональным неравенством.
При решении иррациональных неравенств, как правило, приходится возводить обе
части неравенства в натуральную степень. Такого рода преобразования могут
привести к неравенствам, которые не равносильны исходному, и посколько множество
решений в большинстве случаев представляет бесконечное множество, невозможно
провести проверку полученых решений подстановкой. Единственный способ, который
гарантирует правильный ответ, состоит в применении исключительно равносильных
преобразований неравенств. В связи с этим, приведем соответсвующие утверждения,
которые часто исппользуются при решении иррациональных неравенств (во всех
утверждениях n - натуральное число).
A1. Неравенство
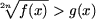 равносильно совокупности систем
равносильно совокупности систем

|

|
g(x) < 0, |
| f(x) ≥ 0, |

|
g(x) ≥ 0, |
|
f(x) > [g(x)]2n.
|
Замечание. Из утверждения A1 следует что
неравенство
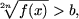 при b ≥ 0 равносильно неравенству f(x) >
[b]2n, а при b < 0, равносильно неравенству
f(x) ≥ 0.
при b ≥ 0 равносильно неравенству f(x) >
[b]2n, а при b < 0, равносильно неравенству
f(x) ≥ 0.
A2. Неравенство
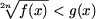 равносильно следующей системе неравенств
равносильно следующей системе неравенств

|
g(x) > 0,
|
|
f(x) ≥ 0,
|
|
f(x) < [g(x)]2n.
|
Замечание.. Из утверждения A2 следует, что если
правая часть неравенства есть число b (g(x) = b),
то
- 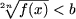 Ы 0 ≤
f(x) < [b]2n, если b > 0
Ы 0 ≤
f(x) < [b]2n, если b > 0
|
- неравенство
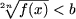 не имеет решений, если b ≤ 0.
не имеет решений, если b ≤ 0.
|
A3. Неравенство
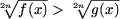 равносильно системе неравенств
равносильно системе неравенств

|
f(x) > g(x), |
|
g(x) ≥ 0.
|
A4. Неравенство
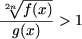 равносильно системе неравенств
равносильно системе неравенств

|
f(x) > [g(x)]2n,
|
|
g(x) > 0.
|
A5. Неравенство
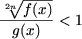 равносильно следующей совокупности систем
равносильно следующей совокупности систем

|

|
g(x) < 0,
|
|
f(x) ≥ 0,
|

|
g(x) > 0,
|
|
f(x) ≥ 0,
|
|
f(x) < [g(x)]2n.
|
A6. Неравенство
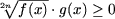 равносильно совокупности
равносильно совокупности

|

|
f(x) = 0,
|
|
x О D(g),
|

|
f(x) > 0,
|
|
g(x) ≥ 0,
|
где D(g) означает область определения функции g.
A7. Неравенство
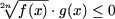 равносильно совокупности
равносильно совокупности

|

|
f(x) = 0,
|
|
x О D(g),
|

|
f(x) > 0,
|
|
g(x) ≤ 0.
|
A8. Неравенства
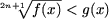 и f(x) <
[g(x)]2n+1
равносильны.
и f(x) <
[g(x)]2n+1
равносильны.
A9. Неравенства
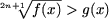 и f(x) >
[g(x)]2n+1
равносильны.
и f(x) >
[g(x)]2n+1
равносильны.
Замечание. Если m нечетное число, то
f(x) < g(x) Ы
[f(x)]m <
[g(x)]m,
f(x) > g(x) Ы
[f(x)]m >
[g(x)]m,
т.е. при возведении в нечетную степень знак неравенства не изменяется.
Расмотрим несколько примеров.
Пример 1. Решить неравенства
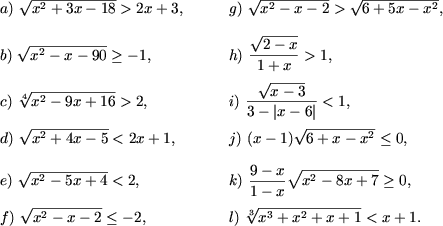
Решение.
a) Используя утверждение A1 (в данном случае
f(x) = x2 + 3x - 18, a
g(x) = 2x + 3) получим
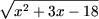 >
2x + 3 >
2x + 3
|
|
Ы

|

|
x2 + 3x - 18 ≥ 0,
|
|
2x + 3 < 0,
|

|
x2 + 3x - 18 > (2x + 3)2,
|
|
2x + 3 ≥ 0,
|
|
Ы

|
x О (-Ґ,-6],
|
|
x О Ж,
|
|
Ы |
Ы x О
(-Ґ,-6].
Действительно, поскольку
x2 + 3x - 18 ≥ 0
Ы
(x + 6)(x - 3) ≥ 0,
решение первого неравенства есть множество
x О
(-Ґ;-6]И[3;+Ґ).
Решения второго неравенства системы x О
(-Ґ,-3/2), следовательно,
решение первой системы совокупности неравенств есть множество
x О (-Ґ,-6].
Первое неравенство второй системы совокупности не имеет решений
x2 + 3x - 18 > (2x + 3)2
Ы
x2 + 3x - 18 >
4x2 + 12x + 9
Ы
Ы
3x2 + 9x + 27 < 0
Ы
x2 + 3x + 9 < 0
Ы
x О Ж
и, следовательно, вторая система совокупности не имеет решений.
Таким образом множество решений исходного неравенства есть
(-Ґ,-6].
b) Заметим, что правая часть неравенства есть отрицательное число, а левая
часть (как только существует - x2 - x - 90 ≥ 0)
получает неотрицательные значения. Таким образом (см. замечание к утверждению
A1 множество решений исходного неравенства находится
решая неравенство
x2 - x - 90 ≥ 0,
или
(x + 9)(x - 10) ≥ 0,
откуда x О
(-Ґ,-9]И[10,+Ґ).
c) Возводим обе части неравенства в четвертую степень и получим равносильное
неравенство (см. замечание к утверждению A1)
x2 - 9x + 16 > 16,
или
x2 - 9x > 0,
откуда x О
(-Ґ,0)И(9,+Ґ).
d) Используя утверждение A2
(здесь f(x) = x2 + 4x - 5 и
g(x) = 2x - 3) получим
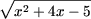 < 2x + 1 < 2x + 1
|
|
Ы

|
2x + 1 ≥ 0,
|
|
x2 + 4x - 5 ≥ 0,
|
|
x2 + 4x - 5 < (2x + 1)2,
|
|
Ы

|
|
x ≥ -1/2,
|

|
x ≤ -5,
|
|
x ≥ 1,
|
|
3x2 + 6 > 0,
|
|
Ы
|
Ы

|
x ≥ 1,
|
Ы
x ≥ 1.
|
|
x О R,
|
e) Используя замечание к утверждению A2 получим
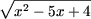 < 2 < 2
|
|
Ы

|
x2 - 5x + 4 < 4,
|
|
x2 - 5x + 4 ≥ 0,
|
|
Ы

|
x2 - 5x < 0,
|
|
x2 - 5x + 4 ≥ 0
|
|
Ы

|
|
0 < x < 5,
|

|
x ≤ 1,
|
|
x ≥ 4,
|
|
Ы
|
Ы
x О (0;1]И[4;5).
f) Неравенство не имеет решений, поскольку левая часть неравенства в
ОДЗ есть выражение, принимающие неотрицательные значения и,
следовательно, не может быть меньше или равно отрицательного числа.
g) Используя утверждение
A3 (здесь f(x) =
x2 - x - 2 и
g(x) = 6 + 5x - x2) получим
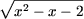 > >
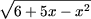
|
|
Ы

|
x2 - x - 2 > 6 + 5x - x2,
|
|
6 + 5x - x2 ≥ 0,
|
|
Ы

|
x2 - 3x - 4 > 0,
|
|
x2 - 5x - 6 ≤ 0,
|
|
Ы
|
Ы

|

|
x < -1,
|
Ы
x О (4,6].
|
|
x > 4,
|
|
-1 ≤ x ≤ 6,
|
h) Согласно утверждению A4
|
|
Ы

|
2 - x > (x + 1)2,
|
|
x + 1 > 0,
|
|
Ы

|
x2 + 3x - 1 < 0,
|
|
x > -1,
|
|
Ы
|
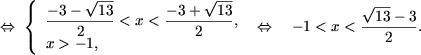
i) Используя утверждение
A5 получим следующую совокупность систем

|

|
3 - |x - 6| < 0,
|
|
x - 3 ≥ 0,
|

|
3 - |x - 6| > 0,
|
|
x - 3 ≥ 0,
|
|
x - 3 < (3 - |x - 6|)2.
|
Решая первую систему, получим

|
|x - 6| > 3,
|
|
x ≥ 3,
|
|
Ы

|

|
x - 6 > 3,
|
Ы

|

|
x > 9,
|
Ы
x > 9.
|
|
x - 6 < -3,
|
x < 3,
|
|
x ≥ 3,
| |
x ≥ 3,
|
Решая вторую систему совокупности, получим

|
|x - 6| < 3,
|
Ы

|
-3 < x - 6 < 3,
|
Ы
|
|
x ≥ 3,
|
x ≥ 3,
|
|
x - 3 < 9 - 6|x - 6| + x2 - 12x + 36,
|
x2 - 6|x - 6| - x + 48 > 0,
|
Ы

|
3 < x < 9,
|
|
x2 - 6|x - 6| - x + 48 > 0,
|
|
Ы

|

|
3 < x ≤ 6,
|
Ы
|
|
x2 + 6(x - 6) - x + 48 > 0,
|

|
6 < x < 9,
|
|
x2 - 6(x - 6) - x + 48 > 0,
|
|
Ы

|

|
3 < x ≤ 6,
|
Ы

|

|
3 < x ≤ 6,
|
Ы
3 < x < 9.
|
|
x2 + 5x + 12 > 0,
|
x О R
|

|
6 < x < 9,
|

|
6 < x < 9,
|
|
x2 - 7x + 84 > 0,
|
x О R,
|
т.е. решение исходного неравенства есть
x О
(3;9)И(9;+Ґ).
j) Согласно утверждению A7 получим:
(x - 1)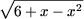 ≤ 0
≤ 0
|
|
Ы

|

|
6 + x - x2 = 0,
|
Ы
|
|
x О R.
|

|
6 + x - x2 > 0,
|
|
x - 1 ≤ 0,
|
Ы

|

|
x = -2,
|
Ы
x О [-2;1]И{3}.
|
|
x = 3,
|

|
-2 < x < 3,
|
|
x ≤ 1,
|
k) Используя утверждение A6 получим:
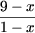
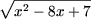 ≥ 0
≥ 0
|
|
Ы

|

|
x2 - 8x + 7 = 0,
|
Ы
|
|
x ≠ 1,
|

|
x2 - 8x + 7 > 0,
|
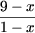 ≥ 0,
≥ 0,
|
Ы

|

|

|
x = 1,
|
Ы

| |
x = 7,
|

|
x < 1,
|
|
x ≥ 9,
|
|
Ы x О
(-Ґ,1)И{7}И[9,+Ґ).
|
|
x = 7,
|
|
x ≠ 1,
|

|

|
x < 1,
|
|
x > 7,
|

|
x ≥ 9,
|
|
x < 1,
|
l) Возведя обе части неравенства в куб получим равносильное неравенство (см.
утверждение A9)
x3 + x2 + x + 1 <
x3 + 3x2 + 3x + 1
или
2x2 + 2x > 0,
откуда x < -1 или x > 0.
В дальнейшем рассмотрим применение метода подстановки.
Пример 2. Решить неравенства
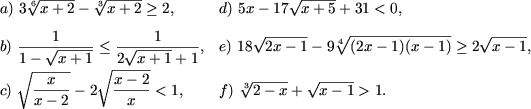
Решение. a) Положив
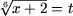 (t ≥ 0),
и тем самым
(t ≥ 0),
и тем самым 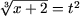 ,
получим неравенство ,
получим неравенство
3t - t2 ≥ 2,
или
t2 - 3t + 2 ≤ 0,
откуда
1 ≤ t ≤ 2.
Следовательно, исходное неравенство равносильно двойному неравенству
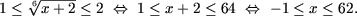
b) Положив
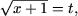 t ≥ 0 и используя метод интервалов получим
t ≥ 0 и используя метод интервалов получим
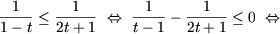
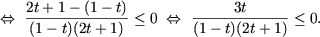
Поскольку t ≥ 0,
влечет 2t + 1 ≥ 1, последнее неравенство равносильно
системе

|
t = 0,
|
|
1 - t < 0,
|
откуда получим t = 0 и t > 1. Таким образом:
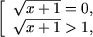 откуда x = -1 и x > 0. Следовательно,
x О
{-1}И(0,+Ґ).
откуда x = -1 и x > 0. Следовательно,
x О
{-1}И(0,+Ґ).
c) Заметим, что данное неравенство содержит взаимно обратные выражения. Положив
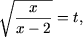 тогда
тогда
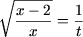 получим неравенство
получим неравенство
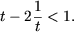
Так как t > 0, последнее неравенство равносильно следующему
t2 - t - 2 < 0,
откуда -1 < t < 2. Так как t > 0,
получим 0 < t < 2, или
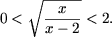
Последнее неравенство равносильно системе
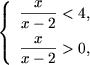 или
или
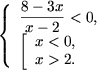
|
Ы

|

|
x > 8/3,
|
|
x < 2,
|

|
x < 0,
|
|
x > 2,
|
|
откуда x О
(-Ґ;0)И(8/3;+Ґ).
d) Запишем неравенство (добавив и вычтя 25) следующим образом:
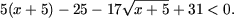
Обозначив
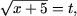 (тогда x + 5 = t2) получим квадратное неравенство
(тогда x + 5 = t2) получим квадратное неравенство
5t2 - 17t + 6 < 0,
откуда
2/5 < t < 3,
или
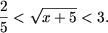
Поскольку все части двойного неравенства положительны, возведя в квадрат
получим равносильное неравенство
4/25 < x + 5 < 9,
откуда x О
(-421/25;4).
e) ОДЗ неравенства есть x ≥ 1.
На ОДЗ неравенство равносильно следуещему
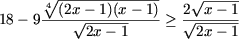 или
или
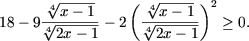
Положив
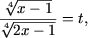 получим квадратное неравенство
получим квадратное неравенство
18 - 9t - 2t2 ≥ 0
решения которого -6 ≤ t ≤ 3/2. Так как
t ≥ 0 исходное неравенство равносильно следующему
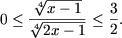
Используя утверждения A1 и
A2 получим
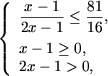 откуда x ≥ 1.
откуда x ≥ 1.
f) Положив
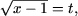 тем самым x - 1 = t2 и
тем самым x - 1 = t2 и
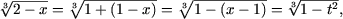 получим неравенство
получим неравенство
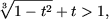 или
или
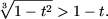
Возводя в куб получим равносильное неравенство (см. утвеждение
A9)
1 - t2 > (1 - t)3,
или
|
(1 - t)(1 + t) - (1 - t)3 > 0,
|
|
(1 - t)(1 + t - (1 - t)2) > 0,
|
|
(1 - t)(1 + t - 1 + 2t - t2) > 0,
|
|
(1 - t)t(3 - t) > 0.
|
Поскольку t ≥ 0, последнее неравенство равносильно системе

|
(1 - t)(3 - t) > 0,
|
|
t ≠ 0,
|
откуда следует совокупность

| |
t > 3,
|

|
t < 1,
|
|
t ≠ 0,
|
или
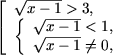 откуда
откуда

|
x - 1 > 9,
|
|
0 < x - 1 < 1,
|
или

|
x > 10,
|
|
1 < x < 2.
|
то есть x О
(1;2)И(10;+Ґ).
Часто используется следующий способ решения иррациональных неравенств: с
помощью преобразований сохраняющих равносильность, исходное неравенство
сводится к неравенствам которые фигурируют в утверждениях
A1-A9, после чего
применяется соответвующее утверждение.
Пример 3. Решить неравенства
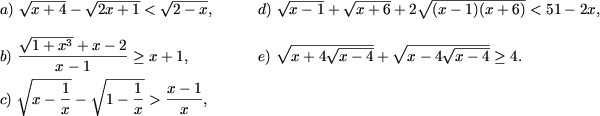
Решение. a) Решив систему (условие существования радикалов второго
порядка)

|
x + 4 ≥ 0,
|
|
2x + 1 ≥ 0,
|
|
2 - x ≥ 0.
|
находим ОДЗ неравенства: [- 1/2;2]
В ОДЗ неравенство равносильно следующему

Поскольку обе части неравенства положительны в ОДЗ, возводя в квадрат,
получим равносильное неравенство:
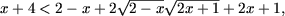 или
или
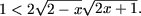
Еще раз возводя в квадрат и учитывая ОДЗ получим

|
1 < 4(2 - x)(2x + 1),
|
|
-1/2 ≤ x
≤ 2,
|
или

|
8x2 - 12x - 7 < 0,
|
|
-1/2 ≤
x ≤ 2,
|
откуда
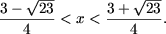
b) Запишем неравенство следующим образом
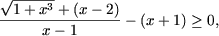 или
или
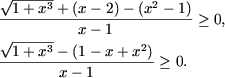
Так как 1 + x3 = (1 + x)(1 - x +
x2) и 1 - x + x2 > 0 для любого
x О R, неравенство
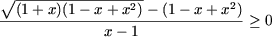 эквивалентно следующему
эквивалентно следующему

Разделив на 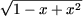 (это выражение положительно для любого x О
R)получим неравенство
(это выражение положительно для любого x О
R)получим неравенство
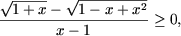 равносильное совокупности систем неравенств
равносильное совокупности систем неравенств
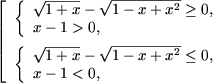 или, учитывая утверждение A3,
или, учитывая утверждение A3,

|

|
1 + x ≥ 1 - x + x2,
|
|
1 - x + x2 ≥ 0,
|
|
x > 1,
|

|
1 + x ≤ 1 - x + x2,
|
|
1 + x ≥ 0,
|
|
x < 1,
|
откуда следует

|

|
x2 - 2x ≤ 0,
|
|
x О R,
|
|
x > 1,
|

|
x2 - 2x ≥ 0,
|
|
x > -1,
|
|
x < 1,
|
|
Ы

|
1 < x ≤ 2,
|
|
-1 < x ≤ 0.
|
|
Таким образом, множество решений исходного неравенства есть
x О (-1;0]И(1;2].
c) ОДЗ данного неравенства x О
[-1;0)И[1;+Ґ),
определяется решая систему неравенств
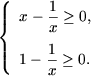
Запишем неравенство в виде
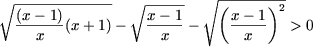 или, используя следующее свойство радикалов четной степени:
или, используя следующее свойство радикалов четной степени:
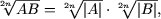 (AB ≥ 0),
(AB ≥ 0),
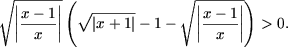
Последнее неравенство, учитывая что в ОДЗ x + 1 ≥ 0 и
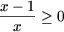 и, следовательно |x + 1| = x + 1,
и, следовательно |x + 1| = x + 1,
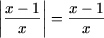 ,
равносильно системе ,
равносильно системе
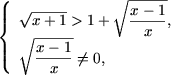 которая решается следующим образом
которая решается следующим образом
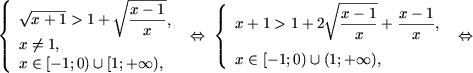
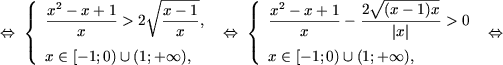
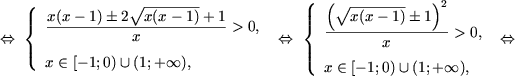
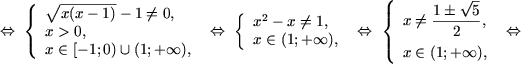
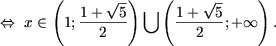
d) Пусть
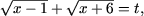 тогда
тогда
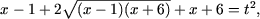 откуда
откуда
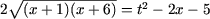 и неравенство принимает вид
и неравенство принимает вид
t + t2 - 5 < 51
или
t2 + t - 56 < 0,
откуда -8 < t < 7. Так как t > 0
(сумма двух радикалов четной степени), остается t < 7 или
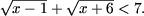
Последнее неравенство можно решить аналогично примеру
3a):
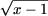 + +
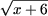 < 7 < 7
|
Ы

|
x - 1 + 2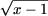 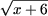 + x + 6 < 49, + x + 6 < 49,
|
|
x-1 ≥ 0,
|
|
x+6 ≥ 0,
|
|
Ы
|
|
|
Ы

|
(x-1)(x+6) < (22-x)2,
|
|
22-x > 0,
|
|
x ≥ 1,
|
|
Ы
|
Ы

|
x < 10,
|
Ы 1 ≤ x < 10,
|
|
1 ≤ x < 22,
|
или другим способом: заметим что для x = 10,
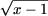 + +
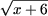 = 7,
следовательно, поскольку функции f(x) = = 7,
следовательно, поскольку функции f(x) =
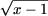 + +
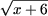 является возрастающей, для x ≥ 10 неравенства не имеет решений.
Учитывая ОДЗ запишем множество решений
x О [1;10).
является возрастающей, для x ≥ 10 неравенства не имеет решений.
Учитывая ОДЗ запишем множество решений
x О [1;10).
e) Так как
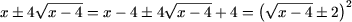 неравенство равносильно следующему:
неравенство равносильно следующему:
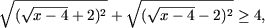 или, учитывая что
или, учитывая что
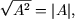
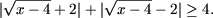
Так как 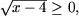 то
то
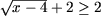 и, следовательно
и, следовательно
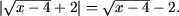 Таким образом,
Таким образом,
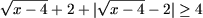 или
или
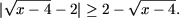
Так как |a| ≥ -a,
для любого a О R
следует что множество решений исходного неравенства совпадает с
ОДЗ, то есть x ≥ 4.
Упражнения
Решить неравенства:
-
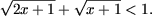
-
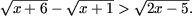
-
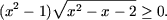
-
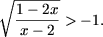
-
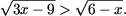
-

-

-

-

-

-
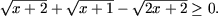
-
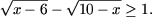
-
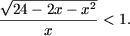
-
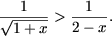
-

-
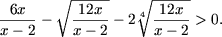
-

-
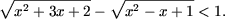
-
-

| Заглавная страница |
Руководство пользователя |
Практикум абитуриента |
Учебные программы |
| Математический кружок |
Занимательная математика|
Формулы, словари |
Новости |
|Странички истории |
Экзамены, тесты |
Библиография |
Ссылки |
Карта |

|
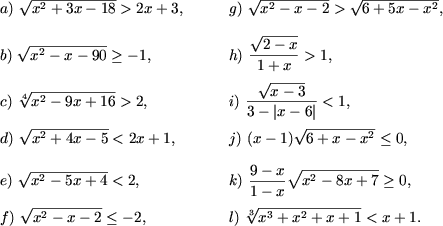
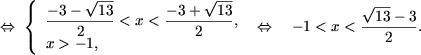
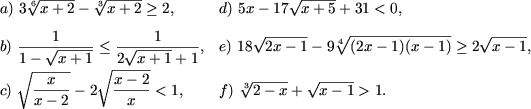
![]() (t ≥ 0),
и тем самым
(t ≥ 0),
и тем самым ![]() ,
получим неравенство
,
получим неравенство
![]() t ≥ 0 и используя метод интервалов получим
t ≥ 0 и используя метод интервалов получим
![]() тогда
тогда
![]() получим неравенство
получим неравенство
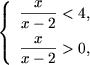
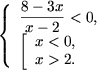
![]() (тогда x + 5 = t2) получим квадратное неравенство
(тогда x + 5 = t2) получим квадратное неравенство
![]() получим квадратное неравенство
получим квадратное неравенство
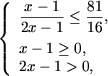
![]() тем самым x - 1 = t2 и
тем самым x - 1 = t2 и
![]() получим неравенство
получим неравенство
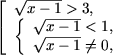
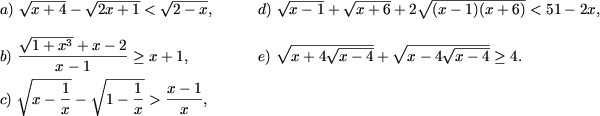
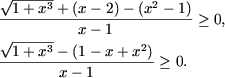
![]() (это выражение положительно для любого x О
R)получим неравенство
(это выражение положительно для любого x О
R)получим неравенство
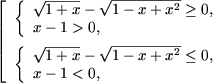
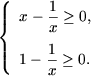
![]() и, следовательно |x + 1| = x + 1,
и, следовательно |x + 1| = x + 1,
![]() ,
равносильно системе
,
равносильно системе
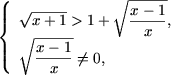
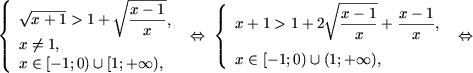
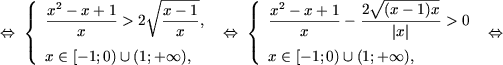
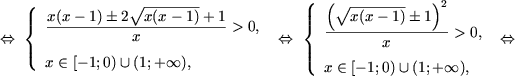
![]() тогда
тогда
![]() откуда
откуда
![]() и неравенство принимает вид
и неравенство принимает вид
![]() то
то
![]() и, следовательно
и, следовательно
![]() Таким образом,
Таким образом,