Уравнение, которое содержит неизвестное в показателе степени, называется показательным уравнением.
Самое простое показательное уравнение имеет вид
| (1) |
Утверждение 1. Уравнение (1) имеет единственное решение x = logab при b > 0 и не имеет решений при b ≤ 0.
Пример 1. Решить уравнения:
Решение. a) Множество решений данного уравнения пусто, так как левая часть уравнения положительна при любом x О R (см. свойства показательной функции), а правая часть есть отрицательное число.
b) Используя утверждение 1 получим x = log24, то есть x = 2.
c) Аналогично предыдущему примеру получим x = log25.
Замечание. Из утверждения 1 следует что показательное уравнение вида
| (2) |
Пример 2. Решить уравнения
Решение. a) Согласно замечанию к утверждению 1
b) Поскольку log39 = 2, данное уравнение равносильно следующему уравнению
|
Ы | x2-x = 2, | Ы |
|
x2-x-2 = 0, | Ы |
|
x = -1, | ||
| x2-x = -2, | x2-x+2 = 0, | x = 2. |
c) Логарифмируя по основанию 5 (обе части уравнения положительны), получим
При решении показательных уравнений используется следующее утверждение о равносильности уравнений (см., например, [2]).
Утверждение 2. При a > 0, a ≠ 1, уравнения
| (3) |
Замечание. Уравнение вида
Некоторые показательные уравнения сводятся к уравнениям вида (1)-(3) с помощью равенств
Пример 3. Решить уравнения
|
a) |
c) |
|
b) | d) 32x-1 = 7x+1. |
Решение. a) Используя равенства E1-E3 и утверждение 2 получим
b) Так как ![]() (ab ≠ 0), то
(ab ≠ 0), то
![]() Используя свойства E4,
E3 и E1, получим
Используя свойства E4,
E3 и E1, получим
c) Так как 43x+1 =
41·43x =
4·(43)
x = 4·64x,
![]() ,
то уравнение примет вид
,
то уравнение примет вид
d) Используя замечание к утверждению 2, получим
Показательные уравнения вида
| (4) |
|
|
(5) |
|
|
Пример 4. Решить уравнения
Решение. a)
2x+3·2x-4 = 76
Ы
![]() Обозначая t = 2x получим линейное уравнение
Обозначая t = 2x получим линейное уравнение
b) Перепишем уравнение в виде
Обозначая t = 3x (тогда 9x = t2) получим алгебраическое уравнение
c) Обозначим ![]() ,
тогда
,
тогда ![]() В результате получим квадратное уравнение
В результате получим квадратное уравнение
d) Так как 21+x =
2·2x,
![]() , то после подстановки
t = 2x, уравнение примет вид
, то после подстановки
t = 2x, уравнение примет вид
Умножив обе части уравнения на t (t > 0), получим квадратное уравнение
 и
t2 = 8. Поскольку t1 < 0, остается
и
t2 = 8. Поскольку t1 < 0, остается
e) Обозначив ![]() (при x О (-Ґ,0]
И[2,+Ґ),
x2-2x ≥ 0 и следовательно
t ≥ 1), получим уравнение
(при x О (-Ґ,0]
И[2,+Ґ),
x2-2x ≥ 0 и следовательно
t ≥ 1), получим уравнение
Возводя в квадрат (обе части уравнения неотрицательны при x О (-Ґ;0]И[2;+Ґ) получим равносильное уравнение
Уравнение вида
Пример 5. Решить уравнения
Решение. a) Записав уравнение в виде
Обозначив ![]() получим квадратное уравнение
получим квадратное уравнение
Таким образом
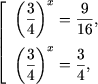
b) Перепишем уравнение в виде
Обозначая ![]() получим квадратное уравнение
получим квадратное уравнение
При решении некоторых показательных уравнений полезно выделить общий множитель.
Пример 6. Решить уравнения
| a) 2x+1 - 2x + 2x-2 - 2x-3 = 9, |
| b) 2x+1 - 2x+2 - 2x+3 = 5x - 5x+1, |
| c) x2·2x+1 + 2|x-3|+2 = x2·2|x-3|+4 + 2x-1. |
Решение. a) Перепишем уравнение в виде
b) Аналогично примеру 6a, получим
c) Запишем уравнение в виде
| 4x2-1 = 0, | |
| 2x-1 = 2|x-3|+2. |
Из первого уравнения совокупности находим x1 = -1/2, x2 = 1/2. Второе решаем используя свойства модуля
Некоторые показательные уравнения решаются особыми методами.
Пример 7. Решить уравнения
| a)
|
d) 4x+(x-1)2x = 6-2x, | g)
|
| b) 5x-2 = 8-x, | e) x2+x+2 = 2·2x-4x, | h)
|
| c) 3x+4x = 5x, | f)
|
i)
|
Решение. a) Заметим, что
![]() .
Используя подстановку
.
Используя подстановку
![]() (тогда
(тогда ![]() )
получим квадратное уравнение
)
получим квадратное уравнение
b) Заметим, что x = 3 является решением данного уравнения. Других корней уравнение не имеет. Действительно, левая часть уравнения представляет строго возрастающую функцию, а правая - строго убывающую функцию. Графики этих функций могут иметь не более одной точки пересечения. Следовательно x = 3 - единственное решение уравнения.
c) Заметим, что x = 2 - корень данного уравнения. Докажем, что других решений уравнение не имеет. Перепишем уравнение в виде:
d) Обозначим t = 2x и решим квадратное уравнение относительно t:
Дискриминант этого уравнения равен D = (x-1)2-4(2x-6) = x2-10x+25 = (x-5)2, и значит его корни имеют вид
e) Перепишем уравнение в виде
f) Заметим, что уравнение имеет решение лишь при x > 0. Тогда правая часть уравнения
Следовательно, исходное уравнение имеет единственное решение x = 1.
g) Заметим, что при x О (-Ґ,-1/2] уравнение не имеет решений (в этом случае левая часть уравнения отрицательна). При x О (-1/2;+Ґ) левая часть уравнения (как произведение двух строго возрастающих функций) есть строго возрастающая функция и, следовательно, каждое свое значение принимает лишь один раз. Остается заметить что x = 0 является (единственным) корьнем данного уравнения.
h) Множество допустимых значений данного уравнения имеет вид: {x О N | x > 1}.
Запишем уравнение в виде
i) ОДЗ уравнения есть множество x О R\{0} и (см. предыдущий пример) его корни 3 и -log52.
Уравнения вида
| (6) |
Как правило, областью определения функции [h(x)] f(x) считается множество всех значений x О D(f) для которых h(x) > 0, где D(f) обозначает область определения функции f. Таким образом
|
f(x) = g(x), | |||
| h(x) > 0, | ||||
| h(x) ≠ 1, | ||||
| h(x) = 1, | ||||
| x О D(f) ЗD(g). |
Пример 8. Решить уравнения
Решение. a) Поскольку a2 = |a|2, уравнение можно переписать в виде
| |x-2| > 0, | ||
| |x-2|≠ 1, | ||
| x2+x+1 = 2, | ||
| |x-2| = 1, | ||
| x О ОДЗ. |
b) Учитывая соотношение (x2+x)0 = 1 получим
|
|
|
c) ОДЗ уравнения представляет множество (0;+Ґ). На ОДЗ уравнение равносильно совокупности
| |x-1| > 0, | ||
| |x-1| ≠ 1, | ||
| lg2x-lgx2 = 3. | ||
| |x-1| = 1, | ||
| x > 0. |
Замечание. Иногда функции из (6) рассматриваются на
более широких областях: принимается во внимание, что функция
h(x)f(x)
имеет смысл и при h(x) = 0, f(x) > 0 или при
h(x) < 0, когда f(x)
принимает значения во множестве целых чисел и т.п. (см., например,
[2]-[4]).
Упражнения