Метод математической индукции

Метод математической индукции является важным способом доказательства предложений (утверждений), зависящих от натурального аргумента.

Метод математической индукции состоит в следующем:

Предложение (утверждение) P(n), зависящее от натурального числа n, справедливо для любого натурального n если:

P(1) является истинным предложением (утверждением);
P(n) остается истинным предложением (утверждением), если n увеличить на единицу, то есть P(n + 1) - истинное предложение (утверждение).

Таким образом метод математической индукции предполагает два этапа:

Этап проверки: проверяется, истинно ли предложение (утверждение) P(1).
Этап доказательства: предполагается, что предложение P(n) истинно, и доказывается истинность предложения P(n + 1) (n увеличено на единицу).

Замечание 1. В некоторых случаях метод математической индукции используется в следующей форме:

Пусть m - натуральное число, m > 1 и P(n) - предложение, зависящее от n, n ≥ m.

Если

P(m) справедливо;
P(n) будучи истинным предложением, влечет истинность предложения P(n + 1) для любого натурального n, n ≥ m, тогда P(n) - истинное предложение для любого натурального n, n ≥ m.

В дальнейшем рассмотрим примеры применения метода математической индукции.

Пример 1. Доказать следующие равенства

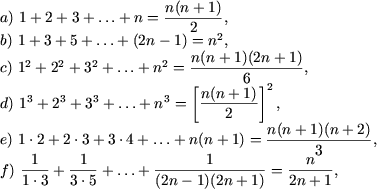
g) формула бинома Ньютона:

где n О N.

Решение. a) При n = 1 равенство примет вид 1=1, следовательно, P(1) истинно. Предположим, что данное равенство справедливо, то есть, имеет место

. Следует проверить (доказать), что P(n + 1), то есть

истинно. Поскольку (используется предположение индукции)

получим

то есть, P(n + 1) - истинное утверждение.

Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального n.

Замечание 2. Этот пример можно было решить и иначе. Действительно, сумма 1 + 2 + 3 + ... + n есть сумма первых n членов арифметической прогрессии с первым членом a₁ = 1 и разностью d = 1. В силу известной формулы , получим

b) При n = 1 равенство примет вид: 2·1 - 1 = 1² или 1=1, то есть, P(1) истинно. Допустим, что имеет место равенство

1 + 3 + 5 + ... + (2n - 1) = n² и докажем, что имеет место P(n + 1): 1 + 3 + 5 + ... + (2n - 1) + (2(n + 1) - 1) = (n + 1)² или 1 + 3 + 5 + ... + (2n - 1) + (2n + 1) = (n + 1)².

Используя предположение индукции, получим

1 + 3 + 5 + ... + (2n - 1) + (2n + 1) = n² + (2n + 1) = (n + 1)².

Таким образом, P(n + 1) истинно и, следовательно, требуемое равенство доказано.

Замечание 3. Этот пример можно решить (аналогично предыдущему) без использования метода математической индукции.

c) При n = 1 равенство истинно: 1=1. Допустим, что истинно равенство

и покажем, что

то есть истинность P(n) влечет истинность P(n + 1). Действительно,

и, так как 2n² + 7n + 6 = (2n + 3)(n + 2), получим

и, следовательно, исходное равенство справедливо для любого натурального n.

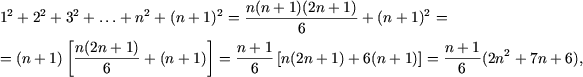
d) При n = 1 равенство справедливо: 1=1. Допустим, что имеет место

и докажем, что

Действительно,

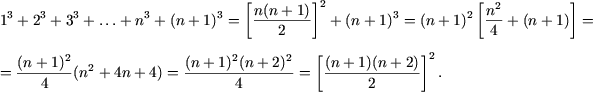
e) Утверждение P(1) справедливо: 2=2. Допустим, что равенство

справедливо, и докажем, что оно влечет равенство

Действительно,

Следовательно, исходное равенство имеет место для любого натурального n.

f) P(1) справедливо: ¹/₃ = ¹/₃. Пусть имеет место равенство P(n):

. Покажем, что последнее равенство влечет следующее:

Действительно, учитывая, что P(n) имеет место, получим

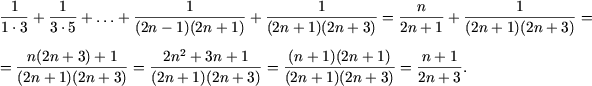
Таким образом, равенство доказано.

g) При n = 1 имеем a + b = b + a и, следовательно, равенство справедливо.

Пусть формула бинома Ньютона справедлива при n = k, то есть,

Тогда

Используя равенство

получим

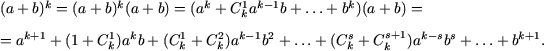
Пример 2. Доказать неравенства

a) неравенство Бернулли: (1 + a)ⁿ ≥ 1 + na, a > -1, n О N.

b) x₁ + x₂ + ... + x_n ≥ n, если x₁x₂· ... ·x_n = 1 и x_i > 0,

c) неравенство Коши относительно среднего арифемтического и среднего геометрического

где x_i > 0,

, n ≥ 2.

d) sin²ⁿa + cos²ⁿa ≤ 1, n О N.

f) 2ⁿ > n³, n О N, n ≥ 10.

Решение. a) При n = 1 получаем истинное неравенство

1 + a ≥ 1 + a. Предположим, что имеет место неравенство

(1 + a)ⁿ ≥ 1 + na

(1)

и покажем, что тогда имеет место и (1 + a)^{n + 1} ≥ 1 + (n + 1)a.

Действительно, поскольку a > -1 влечет a + 1 > 0, то умножая обе части неравенства (1) на (a + 1), получим

(1 + a)ⁿ(1 + a) ≥ (1 + na)(1 + a) или (1 + a)^{n + 1} ≥ 1 + (n + 1)a + na² Поскольку na² ≥ 0, следовательно, (1 + a)^{n + 1} ≥ 1 + (n + 1)a + na² ≥ 1 + (n + 1)a.

Таким образом, если P(n) истинно, то и P(n + 1) истинно, следовательно, согласно принципу математической индукции, неравенство Бернулли справедливо.

b) При n = 1 получим x₁ = 1 и, следовательно, x₁ ≥ 1 то есть P(1) - справедливое утверждение. Предположим, что P(n) истинно, то есть, если adica, x₁,x₂,...,x_n - n положительных чисел, произведение которых равно единице, x₁x₂·...·x_n = 1, и x₁ + x₂ + ... + x_n ≥ n.

Покажем, что это предложение влечет истинность следующего: если x₁,x₂,...,x_n,x_n+1 - (n + 1) положительных чисел, таких, что x₁x₂·...·x_n·x_n+1 = 1, тогда x₁ + x₂ + ... + x_n + x_{n + 1} ≥ n + 1.

Рассмотрим следующие два случая:

1) x₁ = x₂ = ... = x_n = x_n+1 = 1. Тогда сумма этих чисел равна (n + 1), и требуемое неравество выполняется;

2) хотя бы одно число отлично от единицы, пусть, например, больше единицы. Тогда, поскольку x₁x₂· ... ·x_n·x_{n + 1} = 1, существует еще хотя бы одно число, отличное от единицы (точнее, меньше единицы). Пусть x_{n + 1} > 1 и x_n < 1. Рассмотрим n положительных чисел

x₁,x₂,...,x_n-1,(x_n·x_n+1). Произведение этих чисел равно единице, и, согласно гипотезе, x₁ + x₂ + ... + x_n-1 + x_nx_{n + 1} ≥ n. Последнее неравенство переписывается следующим образом: x₁ + x₂ + ... + x_n-1 + x_nx_n+1 + x_n + x_n+1 ≥ n + x_n + x_n+1 или x₁ + x₂ + ... + x_n-1 + x_n + x_n+1 ≥ n + x_n + x_n+1 - x_nx_n+1.

Поскольку

(1 - x_n)(x_n+1 - 1) > 0, то n + x_n + x_n+1 - x_nx_n+1 = n + 1 + x_n+1(1 - x_n) - 1 + x_n =
= n + 1 + x_n+1(1 - x_n) - (1 - x_n) = n + 1 + (1 - x_n)(x_n+1 - 1) ≥ n + 1. Следовательно, x₁ + x₂ + ... + x_n + x_n+1 ≥ n+1, то есть, если P(n) справедливо, то и P(n + 1) справедливо. Неравенство доказано.

Замечание 4. Знак равенства имеет место тогда и только тогда, когда x₁ = x₂ = ... = x_n = 1.

c) Пусть x₁,x₂,...,x_n - произвольные положительные числа. Рассмотрим следующие n положительных чисел:

Поскольку их произведение равно единице:

согласно ранее доказанному неравенству b), следует, что

откуда

Замечание 5. Равенство выполняется если и только если x₁ = x₂ = ... = x_n.

d) P(1) - справедливое утверждение: sin²a + cos²a = 1. Предположим, что P(n) - истинное утверждение:

sin²ⁿa + cos²ⁿa ≤ 1 и покажем, что имеет место P(n + 1). Действительно, sin^{2(n + 1)}a + cos^{2(n + 1)}a = sin²ⁿa·sin²a + cos²ⁿa·cos²a < sin²ⁿa + cos²ⁿa ≤ 1 (если sin²a ≤ 1, то cos²a < 1, и обратно: если cos²a ≤ 1, то sin²a < 1). Таким образом, для любого n О N sin²ⁿa + cos²ⁿ ≤ 1 и знак равенства достигается лишь при n = 1.

e) При n = 1 утверждение справедливо: 1 < ³/₂.

Допустим, что и докажем, что

Поскольку

учитывая P(n), получим

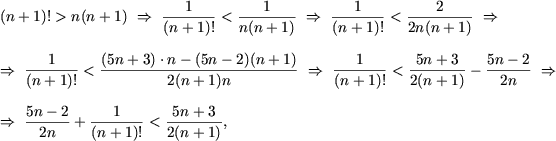
f) Учитывая замечание 1, проверим P(10): 2¹⁰ > 10³, 1024 > 1000, следовательно, для n = 10 утверждение справедливо. Предположим, что 2ⁿ > n³ (n > 10) и докажем P(n + 1), то есть 2ⁿ⁺¹ > (n + 1)³.

Поскольку при n > 10 имеем или , следует, что

2n³ > n³ + 3n² + 3n + 1 или n³ > 3n² + 3n + 1. Учитывая неравенство (2ⁿ > n³), получим 2ⁿ⁺¹ = 2ⁿ·2 = 2ⁿ + 2ⁿ > n³ + n³ > n³ + 3n² + 3n + 1 = (n + 1)³.

Таким образом, согласно методу математической индукции, для любого натурального n О N, n ≥ 10 имеем 2ⁿ > n³.

Пример 3. Доказать, что для любого n О N

a) n(2n² - 3n + 1) делится на 6,

b) 6^2n-2 + 3ⁿ⁺¹ + 3^n-1 делится на 11.

Решение. a) P(1) - истинное утверждение (0 делится на 6). Пусть P(n) справедливо, то есть n(2n² - 3n + 1) = n(n - 1)(2n - 1) делится на 6. Покажем, что тогда имеет место P(n + 1), то есть, (n + 1)n(2n + 1) делится на 6. Действительно, поскольку

n(n + 1)(2n + 1) = n(n - 1 + 2)(2n - 1 + 2) = (n(n - 1) + 2n)(2n - 1 + 2) =

= n(n - 1)(2n - 1) + 2n(n - 1) + 2n(2n + 1) = n(n - 1)(2n - 1) + 2n·3n =

= n(n - 1)(2n - 1) + 6n²

и, как n(n - 1)(2n - 1), так и 6n² делятся на 6, тогда и их сумма n(n + 1)(2n + 1) делится 6.

Таким образом, P(n + 1) - справедливое утверждение, и, следовательно, n(2n² - 3n + 1) делится на 6 для любого n О N.

b) Проверим P(1): 6⁰ + 3² + 3⁰ = 11, следовательно, P(1) - справедливое утверждение. Следует доказать, что если 6^2n-2 + 3ⁿ⁺¹ + 3^n-1 делится на 11 (P(n)), тогда и 6²ⁿ + 3ⁿ⁺² + 3ⁿ также делится на 11 (P(n + 1)). Действительно, поскольку

6²ⁿ + 3ⁿ⁺² + 3ⁿ = 6^2n-2+2 + 3ⁿ⁺¹⁺¹ + 3^n-1+1 = = 6²·6^2n-2 + 3·3ⁿ⁺¹ + 3·3^n-1 = 3·(6^2n-2 + 3ⁿ⁺¹ + 3^n-1) + 33·6^2n-2 и, как 6^2n-2 + 3ⁿ⁺¹ + 3^n-1, так и 33·6^2n-2 делятся на 11, тогда и их сумма 6²ⁿ + 3ⁿ⁺² + 3ⁿ делится на 11. Утверждение доказано.

Индукция в геометрии

Пример 4. Вычислить сторону правильного 2ⁿ-угольника, вписанного в окружность радиуса R.

Решение. При n = 2, правильный 2²-угольник есть квадрат, и в этом случае a₄ = R.

Пусть и определим . Если AB = aў, то AE = ^aў/₂; BD = aўў. По теореме Пифагора, из прямоугольного треугольника DEB

В свою очередь DE = R-EC и

Таким образом,

и, следовательно,

формула перехода от n к n + 1.

В частных случаях

Возникает гипотеза

(2)

Как ранее было показано при n = 1, что эта формула справедлива. Пусть (2) выполняется при n = k. Вычислим . Согласно формуле перехода,

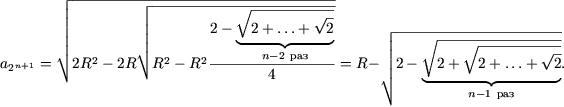
Замечание. Из (2) следует, что длина окружности равна

и, поскольку l = 2pR, получим

Упражнения для самостоятельной работы

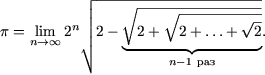
I. Доказать равенства

II. Доказать неравенства

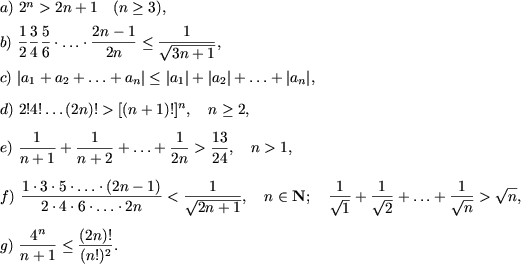
III. Доказать, что при любом натуральном n число a_n делится на b

a) a_n = 5ⁿ⁺³ + 11³ⁿ⁺¹, b = 17,

b) a_n = 11ⁿ⁺² + 12²ⁿ⁺¹, b = 133,

c) a_n = 2n³ + 3n² + 7n, b = 6,

d) a_n = 10ⁿ + 18n - 28, b = 27,

e) a_n = n⁵ - n, b = 30.

IV. Показать, что 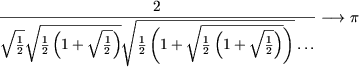(Формула Виета).

V. Вычислить радиусы r_n, R_n вписанной и описанной окружностей правильного 2ⁿ-угольника с периметром p.

VI. Пусть даны n произвольных квадратов. Доказать, что эти квадраты могут быть разрезаны так, чтобы из получившихся частей можно было образовать квадрат.