Принцип крайнего

Принцип крайнего

При решении многих задач ключевой идеей оказывается рассмотрение некоторой крайней или экстремальной величины (элемента, характеристики), связанной с задачей. Этот метод решения задач называется принципом (правилом) крайнего. Приведем несколько примеров.

Задача 1. Доказать бесконечность множества простых чисел вида 4m + 3.

Решение. Предположим противное, т.е. что множество простых чисел вида 4m + 3 конечно. Пусть p₁,ј,p_n - его элементы.

Если n - четное число, то

p₁·p₂·ј·p_n + 2 є (-1)ⁿ + 2 є 3 (mod 4), т.е. p₁·p₂·ј·p_n + 2 = 4m + 3 при некотором m О N. Следовательно это число имеет простой делитель p вида p = 4k + 3 (в самом деле, если все простые делители числа 4m + 3 имеют вид 4k + 1, то и их произведение имеет вид 4k + 1). С другой стороны нетрудно заметить, что ни одно из чисел p₁,p₂,ј,p_n не является делителем числа p₁·p₂·ј·p_n + 2. Отсюда получаем, что p П {p₁,p₂,ј, p_n}. Противоречие с тем, что все простые числа вида 4m+3 содержатся в множестве {p₁,p₂,ј,p_n}.

Если n - нечетное число, то

p₁·p₂·ј·p_n + 4 є (-1)ⁿ + 4 є 3 ( mod 4). Аналогично рассуждая доказывается существование простого числа p вида p = 4k + 3 такого, что p П {p₁,p₂,ј,p_n}. И снова получено противоречие с исходным предположением.

Задача 2. Доказать, что для любого положительного целого числа n число

(1)

не является целым.

Решение. Пусть - максимальная степень тройки, делящая число 2j + 1 (j = 0,1,ј,n). Положим 3^r = max{ | j = 0,1,ј,n}. Покажем, что только для одного j О {0,1,ј,n} имеет место равенство r = r_j. Предположим противное. Тогда для некоторых j ≠ k, j,k, О {0,1,ј,n} имеют место соотношения

2j + 1 = 3^r·s_j, 2k + 1 = 3^r·s_k. Из построения числа 3^r следует, что 3^r+1 > 2n+1. Следовательно 1 ≤ 3^r·s_j < 3^r+1, 1 ≤ 3^r·s_k < 3^r+1. Отсюда получаем, что 1 ≤ s_j ≤ 2, 1 ≤ s_k ≤ 2. Так как s_j ≠ s_k, то одно из чисел s_j, s_k - четное. Полученное противоречие доказывает справедливость утверждения.

Приводя выражение (1) к общему знаменателю получим

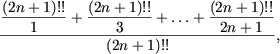
(2)

где (2n + 1)!! = 1·3·ј·(2n + 1).

Пусть r = r_j и 3^m - максимальная степень тройки, делящая число (2n+1)!!. Тогда для каждого k ≠ j из соотношения следует, что . С другой стороны . Значит

следовательно число (2) не целое.

Задача 3. Доказать, что уравнение

x² + y² = 3(z² + t²) (3)
не разрешимо в целых положительных числах.

Решение. Предположим противное, т.е. что существуют решения x, y, z, t уравнения (3) в целых положительных числах. Рассмотрим решение, для которого выражение x² + y² минимально. Из (3) следует, что 3|x² + y². Отсюда получаем, что 3|x и 3|y (это следует из того, что остаток от деления квадрата любого целого числа на 3 равен 0 или 1). Таким образом, x = 3x₁, y = 3y₁. Следовательно

Заметим, что z² + t² < x² + y². Полученное противоречие доказывает справедливость исходного утверждения.

Задача 4. На плоскости задано множество точек M такое, что каждая точка из M является серединой отрезка, соединяющего некоторые две другие точки из M. Докажите, что множество M бесконечно.

Решение. Предположим противное. Введем на плоскости систему прямоугольных координат. Рассмотрим точку из M с максимальной абсциссой. Если таких точек несколько, то рассмотрим ту из них, у которой максимальна (среди точек с максимальной абсциссой) ордината. Обозначим эту крайнюю точку через A(x,y). Она является серединой отрезка, соединяющего некоторые две точки B(x₁,y₁), C(x₂,y₂), принадлежащие M. Из соотношений , x₁ ≤ x, x₂ ≤ x следует, что x₁ = x₂ = x. То есть точки A, B, C имеют одинаковую абсциссу. Поэтому y₁ ≤ y, y₂ ≤ y. Это невозможно, так как , а точки A, B, C - различны. Полученное противоречие доказывает требуемое утверждение.

Задача 5. На каждой стороне произвольного четырехугольника, как на диаметре, построена окружность. Доказать, что четыре построенных круга полностью покроютчетырехугольник.

Решение.

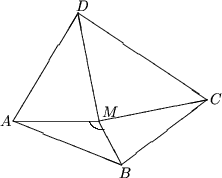
Обозначим данный четырехугольник ABCD (на рисунке он выпуклый, но можно проследить, что приведенное решение проходит и для невыпуклого четырехугольника). Пусть M - произвольная точка внутри четырехугольника. Рассмотрим максимальный угол среди углов РAMB, РBMC, РCMD, РDMA. Пусть это будет, например, угол РAMB. Тогда РAMB ≥ 90^° (в противном случае РAMB + РBMC + РCMD + РDMA < 4·90^° = 360^°). Следовательно точка M покроется кругом, построенном на отрезке AB, как на диаметре.

Задача 6. Докажите, что если длины всех сторон треугольника меньше 1, то его площадь меньше .

Решение.

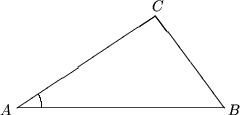
Обозначим данный треугольник через ABC. Пусть РA - его минимальный угол. Тогда РA ≤ 60^° и площадь треугольника оценивается следующим образом

Задача 7. На плоскости проведено n (n ≥ 3) попарно непараллельных прямых, причем через точку пересечения любых двух из них проходит ещё одна из данных прямых. Докажите, что все эти прямые проходят через одну точку.

Решение. Предположим противное. Это означает, что существует прямая из этого семейства и существует точка пересечения других прямых, не принадлежащая ей. Рассмотрим минимальное ненулевое расстояние от точек пересечений прямых до прямых. Пусть это будет расстояние от точки A до прямой l. Через точку A проходят по крайней мере три прямые.

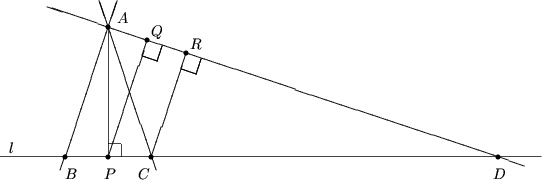
Обозначим их точки пересечения с прямой l через B, C, D. Опустим из точки A перпендикуляр AP на l. Из точек B,C,D по крайней мере две находятся по одну сторону относительно точки P. Пусть это будут точки C, D, причем PC < PD. Из точек P и C опустим перпендикуляры PQ и CR на прямую AD. Так как AP > PQ (гипотенуза прямоугольного треугольника APQ больше его катета) и PQ ≥ CR, следовательно AP > CR. Противоречие.

Задача 8. На плоскости расположено n точек, причем площадь любого треугольника с вершинами в этих точках не превосходит 1. Докажите, что все эти точки можно поместить в треугольник площади 4.

Решение.

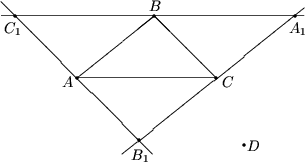
Рассмотрим треугольник максимальной площади с вершинами в данных точках. Пусть это будет треугольник ABC. Через точки A, B, C проведем прямые l_A, l_B, l_C, параллельные сторонам BC, CA, AB соответственно. Обозначим треугольник, образованный прямыми l_A, l_B, l_C через A₁B₁C₁. Площадь этого треугольника в 4 раза больше площади треугольника ABC, следовательно она не превосходит 4. Покажем, что каждая данная точка находится в треугольнике A₁B₁C₁. Предположим противное. Тогда существует точка D из данного множества, находящаяся с некоторой вершиной треугольника A₁B₁C₁ по разные стороны относительно стороны, противолежащей этой вершине. Пусть, например C₁ и D находятся по разные стороны относительно стороны B₁A₁. Тогда расстояние от точки D до AB больше, чем расстояние от точки C до AB. Следовательно площадь треугольника ABD больше площади треугольника ABC, что противоречит выбору треугольника ABC.

Задача 9. Докажите, что любой выпуклый многоугольник площади 1 можно поместить в прямоугольник площади 2.

Решение.

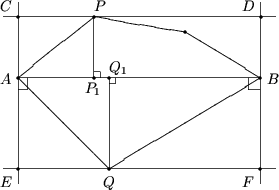
Пусть AB - максимальная диагональ (или сторона) многоугольника. Проведем через точки A и B прямые, перпендикулярные отрезку AB. Из построения отрезка AB следует, что весь многоугольник содержится в полосе, образованной этими прямыми. Проведем прямые CD, EF, параллельные AB, проходящие через некоторые вершины многоугольника и обладающие тем свойством, что многоугольник находится по одну сторону относительно каждой из них. Опустим из точек P и Q перпендикуляры PP₁ и QQ₁ на AB. Площадь исходного многоугольника больше или равна суммы площадей треугольников APB и AQB, т.е. выражения

Отсюда следует, что площадь прямоугольника EFDC, содержащего исходный многоугольник, не превосходит 2.

Задача 10. На плоскости даны четыре точки, не лежащие на одной прямой. Докажите, что хотя бы один из треугольников с вершинами в этих точках не является остроугольным.

Решение.

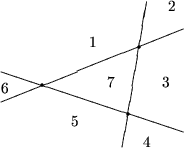
Рассмотрим произвольный треугольник с вершинами в данных точках. Прямые, построеные на сторонах этого треугольника разбивают плоскость на 7 частей. В связи с этим возникают несколько случаев.

I случай.

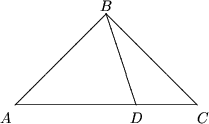
Четвертая точка расположена на одной из прямых. В этом случае некоторые три точки A, B, C образуют треугольник, а четвертая точка D лежит на одной из его сторон. Очевидно, максимальный угол среди РADB, РCDB не является острым. Поэтому по крайней мере один из треугольников ADB, CDB не является остроугольным.

II случай.

Четвертая точка расположена в одной из частей 2,4,6,7. В этом случае существует треугольник ABC, с вершинами в данных точках, содержащий внутри себя данную точку D. Максимальный угол среди РADC, РCDB, РBDA, не меньше 120^°, следовательно по крайней мере один из треугольников ADC, CDB, BDA, не является остроугольным.

III случай.

Четвертая точка расположена в одной из частей 1,3,5. В этом случае четыре данные точки являются вершинами выпуклого четырехугольника, который обозначим ABCD. Максимальный угол среди РABC, РBCD, РCDA, РDAB не меньше 90^°. Следовательно по крайней мере один из треугольников ABC, BCD, CDA, DAB не является остроугольным.

Задача 11. Семь грибников собрали вместе 100 грибов, причем никакие двое не собрали одинакового числа грибов. Докажите, что есть трое грибников, собравших вместе не менее 50 грибов.

Решение. Рассмотрим трех грибников, собравших вместе максимальное (среди всевозможных троек грибников) количество грибов. Если минимальное (из этих трех) количество грибов равно 16, то вместе три грибника собрали грибов не меньше, чем 16 + 17 + 18 = 51. Если указанное минимальное количество не больше 15, то оставшиеся четыре грибника собрали вместе не более 14 + 13 + 12 + 11 = 50 грибов. Отсюда заключаем, что первые трое собрали вместе не менее 50 грибов.

Задача 12. Пусть элементами таблицы n×n являются нули и единицы. Пусть при этом выполнено следующие условие: если на некотором месте таблицы записан нуль, то сумма чисел столбца и строки, содержащих этот нуль, не меньше n. Докажите, что сумма всех n² чисел не меньше .

Решение. Рассмотрим строку или столбец, имеющие минимальную сумму элементов среди всевозможных сумм элементов каждой строки и каждого столбца. Пусть, для определенности, это будет строка с суммой элементов равной k. Если , то сумма элементов каждой строки не меньше и поэтому сумма всех элементов не меньше . Предположим, что . Тогда в данной строке n - k нулей. Следовательно сумма элементов каждого столбца, содержащего один из указанных нулей не меньше n - k. Таких столбцов n - k, поэтому общая сумма содержащихся в них элементов не меньше (n - k)². Сумма элементов в каждом из оставшихся k столбцов не меньше k, поэтому общая сумма содержащихся в них элементов не меньше k². Следовательно сумма всех элементов таблицы не меньше

Задачи для самостоятельного решения

Доказать бесконечность множества простых чисел вида 6m + 5.
Доказать, что для любого целого числа n, n > 1, число не является целым.
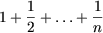
Доказать, что уравнение x² + y² + z² = 2¹⁹⁹⁹ не имеет решений в целых числах.
В некоторой стране 100 аэродромов, причем все попарные расстояния между ними различны. С каждого аэродрома поднимается самолет и летит на ближайший к нему аэродром. Докажите, что ни на один аэродром не может прилететь больше пяти самолетов.
На плоскости дано конечное число точек, причем любая прямая, проходящая через две из данных точек, содержит ещё одну данную точку. Докажите, что все данные точки лежат на одной прямой.
Длины биссектрис треугольника не превосходят 1. Докажите, что его площадь не превосходит .
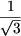Докажите, что в любом выпуклом пятиугольнике найдутся три диагонали, из которых можно составить треугольник.