Прием 2000, тест по математике

1. Решить неравенство

≥ 1

A) x О	B) x О [6;+Ґ)	C) x О И [6;+Ґ)
D) x О	E) x О .

2. Сколько корней уравнения

2sinx·cosx - 3(sinx + cosx) + 3 = 0 находятся на отрезке

. A) один B) ни один C) два D) три E) четыре.

3. Решить неравенство

log_x²2 - 5log_x2 + 6 ≥ 0

A) x О (0;1) И (1;+Ґ)	B) x О (0,1) И (1;] И [;+Ґ)
C) x О (0;1) И [;+Ґ)	D) x О (1;] И [;+Ґ)
E) x О (1;)

4. Найти величины углов треугольника, если известно, что высота и медиана проведенные из одного и того же угла треугольника, делят данный угол на три равные части.

A) 30°, 30°, 120°	B) 45°, 45°, 90°	C) 30°, 60°, 90°
D) 60°, 60°, 60°	E) 25°, 55°, 100°.

5. Какие из следующих утверждений истины?

Для любого треугольника ABC справедливо неравенство cosA + cosB + cosC ≤ ;
Если четырехугольник имеет центр симметрии, то этот четырехугольник является прямоугольником;
В равнобедренном треугольнике центр вписанной окружности этого треугольника совпадает с центром описанной окружности этого треугольника;
В равнобедренной трапеции точка пересечения диагоналей является центром симметрии этой трапеции;
В прямоугольном треугольнике центр описанной ему окружности совпадает с серединой гипотенузы.

Тест подготовлен доцентом МГУ, д.ф.м.н. С.Катаранчук.

Решения

1. Неравенство равносильно следующему

≥ 1 +

Так как обе части последнего неравенства неотрицательны, возведя их в квадрат, получим равносильное неравенство

4x + 1 ≥ 1 + 2

+ 2x + 4 или, x - 2 ≥

Последнее неравенство равносильно следующей системе

	x - 2 ≥ 0,
	(x - 2)² ≥ 2x + 4,
	2x + 4 ≥ 0.

Решив систему

	x ≥ 2,
	x² - 4x + 4 ≥ 2x + 4,
	x ≥ -2,

	x ≥ 2,
	x(x - 6) ≥ 0,

x ≥ 2,

	x ≤ 0,
	x ≥ 6,

получим x ≥ 6.

Следовательно, множество решений неравенства есть множество [6;+Ґ).

Ответ: B.

2. Обозначим sinx + cosx = t, (|t| ≤ ), тогда , и уравнение примет вид

t² - 1 - 3t + 3 = 0 или t² - 3t + 2 = 0, откуда t₁ = 1 и t₂ = 2 (не удовлетворяет условию |t| ≤

). Следовательно sinx + cosx = 1.

Используя метод вспомогательного угла, получим

Поскольку x О , следует что x₁ = 0 и x₂ = и, таким образом, на данном отрезке уравнение имеет два решения.

Ответ: C.

3. Область допустимых значений неравенства есть множество x О (0,1) И (1,+Ґ). Обозначим log_x2 = t и получим квадратное неравенство t² - 5t + 6 ≥ 0 решения которого t ≤ 2 или t ≥ 3. Таким образом

Ответ: B.

4. Пусть в треугольнике ABC BD^AC (BD - высота), BE - медиана (AE = EC = a) РABD = РDBE = РEBC = a.

Поскольку BD высота и биссектриса, DABE равнобедренный и, следовательно BD - медиана,

Из DABD: Используя теорему синусов

или

откуда 4sinacos2a = sin3a, или 4sina(1 - 2sin²a) = sina(3 - 4sin²a).

Так как a ≠ pk, k О Z, то

4 - 8sin²a = 3 - 4sin²a, или 4sin²a = 1 откуда sina = ¹/₂ (sina = -¹/₂ не удовлетворяет условиям задачи) и a = 30°. Следовательно, углы треугольника равны РABC = 3a = 90°, РBAC = 90 - a = 60°, РBCA = 30°.

Ответ: C.

Истинное утверждение. Так как (R (r) - радиус описанной (вписанной) в треугольник окружности), а 2r ≤ R, то
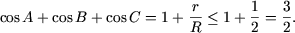
Ложное утверждение. Например, ромб имеет центр симметрии, но не обязательно является прямоугольником.
Ложное утверждение. Например, в прямоугольном треугольнике центр описанной окружности совпадает с серединой гипотенузы, а центр вписанной окружности находится внутри треугольника.
Ложное утверждение. Следует из определения центра симметрии.
Истинное утверждение. Следует из теоремы синусов: 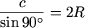Ю c = 2R и (c - гипотенуза, R - радиус описанной окружности).

Ответ: Первое и пятое утверждение истинны.