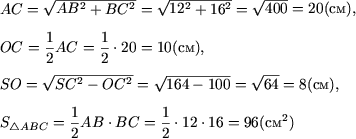Экзамен по математике на бакалавра, 1999, гуманитарный профиль

Время решения - 180 минут

1. Определить, какому числовому множеству принадлежит числовое выражение

Решение. Приведя к общему знаменателю, получим

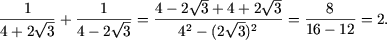
Ответ. Множеству натуральных чисел.

Замечание. Нужно принять во внимание, что N М Z М Q М R М C...

2. Написать полиномиальное уравнение третьего порядка, если известно, что одним из корней этого уравнения является x = 1.

Решение. Пусть корнями искомого уравнения являются x₁ = 1, x₂ = 2 и x₃ = 3. Тогда, согласно теореме Безу,

P₃(x) = (x - 1)(x - 2)(x - 3) или P₃(x) = x³ - 6x² + 11x - 6. В общем случае, если коэффициэнты многочлена a₀x³ + a₁x² + a₂x + a₃ удовлетворяют условию a₀ + a₁ + a₂ + a₃ = 0, то x = 1 есть корень уравнения a₀x³ + a₁x² + a₂x + a₃ = 0.

3. Найти сумму действительных корней уравнения

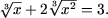
Решение. ОДЗ уравнения есть множество R. Обозначив , получим квадратное уравнение 2t² + t - 3 = 0, решения которого t₁ = 1 и t₂ = -³/₂.

Таким образом,

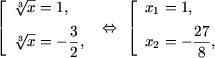
следовательно, сумма действительных корней исходного уравнения равна x₁ + x₂ = -¹⁹/₈.

4. Решить неравенство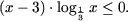

Решение. ОДЗ неравенства есть множество x > 0. Используем обобщенный метод интервалов.

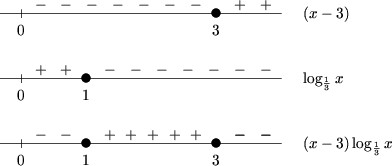
Получим: x О (0,1]И[3;+Ґ).

5. Показать, что парабола y = x² - x + 5,35 не пересекает график функции f(x) = 2sinx + 3.

Решение. Поскольку 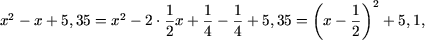область значений функции y = x² - x + 5,35 есть множество [5,1;+Ґ). В то же время, |sinx| ≤ 1 влечет 1 ≤ 2sinx + 3 ≤ 5 и, следовательно, графики данных функций не пересекаются.

6. Определить площадь фигуры, ограниченной графиками функций f(x) = 2 + x - x² и g(x) = 2 - x.

Решение.

Площадь S фигуры, ограниченной графиками функций f(x) = 2 + x - x² и g(x) = 2 - x (см. рисунок) определяется по формуле

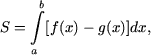
где a и b - пределы интегрирования, которые определяются при решении уравнения f(x) = g(x).

В данном случае

2 + x - x² = 2 - x или x² - 2x = 0 откуда, учитывая, что a < b, получим a = 0, b = 2.

Следовательно,

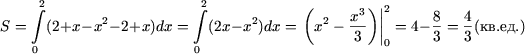
7. При каких действительных значениях значениях параметра a система

	ax + y + z = 1,
	3x + ay + z = 1,
	3x + y + az = 1,

имеет единственное решение?

Решение. Согласно правилу Крамера, данная система будет иметь единственное решение, тогда и только тогда, когда ее главный определитель будет отличен от нуля.

a	1	1	≠ 0.
3	a	1
3	1	a

Раскрывая определитель, получим a³ - 7a + 6 ≠ 0, откуда, учитывая, что a³ - 7a + 6 = a³ - a - 6a + 6 = a(a² - 1) - (6a - 6) = a(a - 1)(a + 1) - 6(a - 1) = = (a - 1)(a² + a - 6) = (a - 1)(a + 2)(a - 3) получим a ≠ 1, a ≠ -2 и a ≠ 3 или a О R\{-2,1,3}.

8. Напишите уравнение касательной к графику функции в точке x₀ = -3.

Решение. Уравнение касательной к графику функции f(x) в точке x₀ есть

y - f(x₀) = f ў(x₀)(x - x₀) где f ў(x₀) - значение производной функции f(x) в точке x₀.

Так как

получим y - 9 = -3(x + 3) или, после элементарных преобразований, y = -3x.

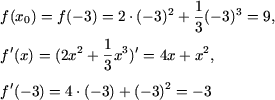
9. В основании треугольной пирамиды - прямоугольный треугольник с катетами 12см и 16см. Найти объем пирамиды, если известно, что боковые ребра равны и имеют длину см.

Решение.

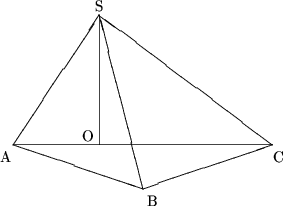
Поскольку все боковые ребра равны, высота пирамиды падает в центр описанной окружности основания, то есть, основание высоты находится в середине гипотенузы AC.

Так как

получим