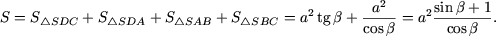Экзамен по математике на бакалавра, 1999, гуманитарный профиль

Время решения - 180 минут

1. Пусть f:R^*®R, Вычислить f(log₂3).

Решение. Используя основное логарифмическое тождество , получим

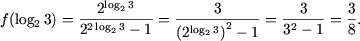
2. Написать уравнение второго порядка с действительными корнями, произведение которых равнялось бы четырем.

Решение. Используя обратную теорему Виета, например, для x₁ = 1 и x₂ = 4 (тогда x₁·x₂ = 4, x₁ + x₂ = 5), получим квадратное уравнение

x² - 5x + 4 = 0.

3. Пусть 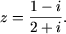Определить, при каких значениях a и b справедливо равенство

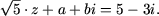
Решение. Так как

то равенство принимает вид

или

откуда, используя определение равенства двух комплексных чисел (z₁ = z₂ Ы Rez₁ = Rez₂ и Imz₁ = Imz₂), получим систему

решение которой

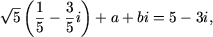
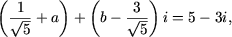
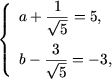
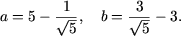
4. Пусть дана функция f(x) = 1-cosx. Вычислить значение выражения

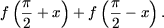
Решение. Используя формулы приведения 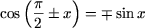, получим

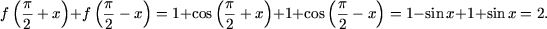
5. При каких действительных значениях параметра m многочлен 2x³ - x² + mx - 2 делится на x - 2.

Решение. Поскольку

f(2) = 2·2³ - 2² + m·2 - 2 = 10 + 2m, решая линейное уравнение 10 + 2m = 0, получим m = -5.

6. Вычислить площадь фигуры, ограниченной графиками функций f(x) = -x² - 4x и g(x) = 4 + x.

Решение.

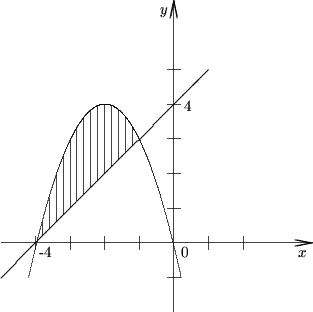
Искомая площадь определяется, используя формулу

где a и b - пределы интегрирования.

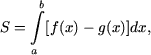
Для определения a и b решим уравнение f(x) = g(x), то есть,

-x² - 4x = 4 + x, или x² + 5x + 4 = 0 откуда, учитывая, что a < b, получим x₁ = a = -4, x₂ = b = -1.

Таким образом,

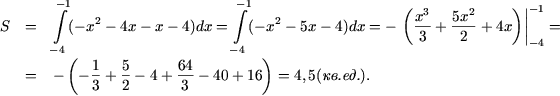
7. Пусть функция f:D®R, (D Ì R), 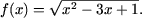Решить уравнение 3f(x) = 2f ¢(x).

Решение. Используя правило нахождения производной сложной функции, находим f ¢(x):

и уравнение примет вид

или 3(x² - 3x + 1) = 2x - 3, откуда следует квадратное уравнение 3x² - 11x + 6 = 0 решения которого x₁ = ²/₃ и x₂ = 3.

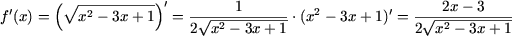
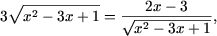
После проверки остается x = 3.

8. Решить неравенство

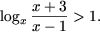
Решение. Используя утверждение 3 из Логарифмические неравенства, получим совокупность систем

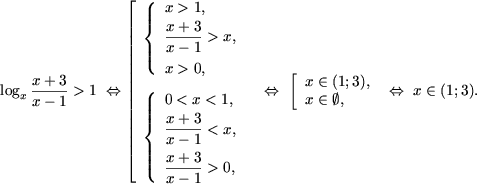
Действительно, первая система совокупности (учитывая, что x > 1) равносильна системе

	x > 1,	или		x > 1,	откуда x Î (1;3).
	x+3 < x(x - 1),			x² - 2x - 3 < 0,

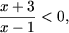Вторая система не имеет решений, так как при x Î (0;1) (первое неравенство) имеем

что противоречит последнему неравенству системы.

Таким образом, множеством решений исходного неравенства является (1;3).

9. Основание пирамиды - квадрат со стороной a. Две боковые грани пирамиды перпендикулярны плоскости основания, а остальные две образуют с ней угол b. Найти площадь боковой поверхности пирамиды.

Решение.

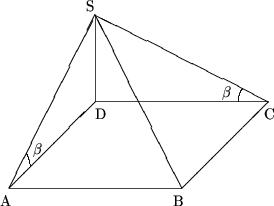
Рассмотрим прямоугольный треугольник SDC (SD ^ DC) и, используя метрические соотношения в прямоугольном треугольнике, получим

SD = CD tg ÐDCS = a tg b, и, поскольку

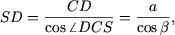
(SD - общая сторона, AD = DC), то

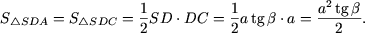
Так как SA ^ AB (SC ^ BC) - следует из теоремы о трех перпендикулярах), имеем

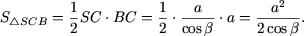
Аналогично,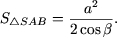

Таким образом, площадь боковой поверхности пирамиды равна