Экзамен по математике на бакалавра, 10 июля 1999, профиль: математика

1. Вычислить

(3 очка)

Решение. Неопределенность вида Ґ - Ґ. Приведя к общему знаменателю, получим

2. Привести пример функции, которая определена и непрерывна на открытом интервале (a,b), но которая неограничена на этом интервале. (3 очка)

Решение.

Действительно, f О C((a,b)) и

3. Пусть z = 1 + i. Определить действительные числа a,b О R, если известно, что z³ = az + b. (4 очка)

Решение. Используя определение равенства двух комплексных чисел, получим

(1 + i)³ = az + b Ы 1 + 3i + 3i² + i³ = a(1 + i) + b Ы 1 + 3i - 3 - i = a + b + ai Ы

Ы -2 - 2i = (a + b) + ai Ы

a+b = -2,

a = 2,

b = -4.

4. Вычислить определенный интеграл

(5 очков).

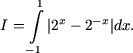
Решение. Заметим, что подинтегральная функция четная и, следовательно, 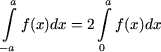. Поскольку для x О [0,1] имеем 2^x - 2^-x ≥ 0, то получим

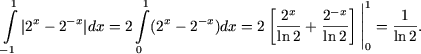
5. Решить уравнение

3+4|cosx| = bcos2x, если известно, что

является одним из его решений. (6 очков)

Решение. Так как x = есть решение уравнения, следует, что

, или

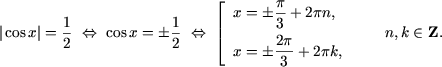
6. Высота прямого кругового конуса равна 6см, а его образующая образует угол в 60° с плоскостью основания. В конусе размещена пирамида, основание которой - прямоугольный равнобедренный треугольник, вписанный в основание конуса, а вершина пирамиды находится на середине одной из образующих конуса. Найти объем пирамиды. (5 очков)

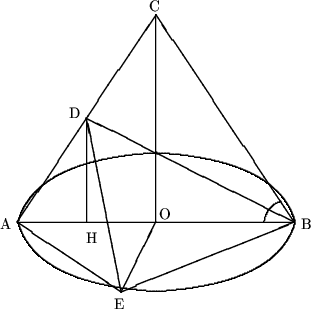
Решение. Рассмотрим прямоугольный треугольник COB (CO^OB). Так как РCBO = 60° (из условий), используя метрические соотношения в треугольнике, получим: (см). Таким образом, гипотенуза AB прямоугольного треугольника AEB (в то же время диаметр окружности радиуса OB) равна (см), а площадь AEB (и площадь основания пирамиды).

(см²). Высота пирамиды DH является средней линией в AOC, и, следовательно, равна половине OC,

Таким образом,

(см³).

7. Прямая x + y - 4 = 0 является касательной к эллипсу

где b О (0,3). Определить значение b и координаты точки касания прямой и эллипса. (6 очков)

Решение. Уравнение касательной к эллипсу в точке (x₀,y₀) есть

или, в данном случае

откуда

Из условия (y = -x + 4) следует

откуда x₀ = ⁹/₄. Поскольку y₀ = 4 - x₀ Ю y₀ = ⁷/₄, используя уравнение эллипса находим b:

откуда 9b² + 49 = 16b², или b² = 7,

, и, поскольку b О (0,3), получим

. Таким образом

, а точка касания M(⁹/₄,⁷/₄).

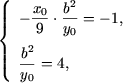
8. Определить член разложения бинома , который не содержит b², если известно, что n - это наибольшее натуральное число, которое удовлетворяет неравенству

(7 очков)

Решение. Исходное неравенство равносильно следующему

Обозначив log₃n = t, получим

Учитывая что t > 0, из последнего неравенства получим 1 < log₃x < 2 Ы 3 < n < 9. Поскольку n О N и является наибольшим из интервала (3;9), следует, что n = 8. Общий член разложения T_k+1 имеет вид

откуда ^k/₃ = 2 или k = 6. Таким образом,

9. Рассмотрим функцию

f:D® R, D М R такую, что

Найти такие a, b чтобы значения функции в точках экстремума равнялись -1 и -2. (8 очков)

Решение. Находим критические точки

Следовательно, f ў(x) = 0 Ю b² - x² = 0 Ю x = ±b.

Заметим, что a ≠ 0, b ≠ 0 (в противном случае нарушаются условия задачи) и в окрестностях точек x = ±b производная меняет знак. Следовательно, точки x = -b и x = b являются точками экстремума.

Получим следующую совокупность систем

		f(b) = -1,
		f(-b) = -2,
		f(b) = -2,
		f(-b) = -1

или

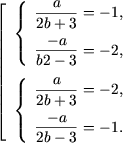
Из первой системы получим a = -4, b = ¹/₂, а из второй a = -4, b = -¹/₂. В обоих случаях функция f равна

10. Пусть ABC - прямоугольный треугольник с прямым углом C. Медиана CP перпендикулярна медиане BQ, а сторона BC равна a. Вычислить длину медианы BQ. (8 очков)

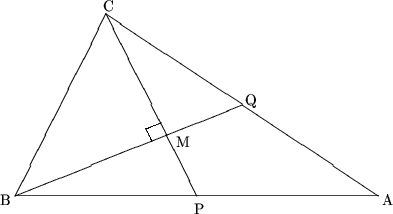
Решение. Пусть РCBA = a. Тогда РBAC = 90°-a. Поскольку CP =¹/₂AB = BP = PA, следует РBCP = a и РACP = 90°-a. Из прямоугольного треугольника CMQ получим РCQB = a. Таким образом, откуда

Так как CQ = ¹/₂AC (BQ - медиана) следует

откуда

Используя теорему Пифагора, получим AB² = a² + 2a², или

Таким образом,