Экзамен по математике на бакалавра, 2003, реальный профиль

Министерство просвещения Республики Молдова
Экзамен по математике на соискание звания бакалавра, 2 июня 2003
Реальный профиль

Время работы: 180 минут.

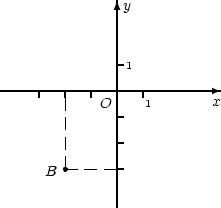
1. Запишите в алгебраической форме комплексное число z, геометрической интерпретацией которого служит точка B.

2. На рисунке представлен график функции f: [−6; 4] ® R. При каких значениях a уравнение f(x) = a имеет три различных действительных корня?

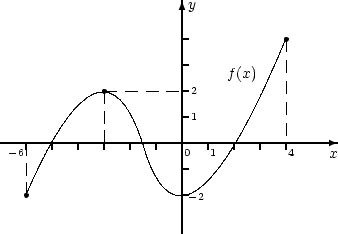
3. Запишите уравнение окружности с диаметром AB, где A(3;2), B(−1; 6).

4. Монету подбрасывают три раза. Какова вероятность того, что два раза выпадет "орел"?

5. Девятый член разложения бинома не содержит x. Вычислите A_n².

6. Вычислите .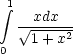

7. Решите неравенство (sin2)^x²-x ≥ sin² 2.

8. Площадь осевого сечения цилиндра равна Q. Найдите площадь его боковой поверхности.

9. Найдите корни многочлена P(X) = X ³ + 2aX ² −5X − a − 9, aÎR, если известно, что остаток от деления P(X) на двучлен (X − 2) равен остатку от деления P(X) на двучлен X+1.

10. Найдите площадь треугольника, образованного биссектрисами координатных углов и касательной к графику функции f:[; ¥) ® R, f(x)= в точке M(3;2).

11. Решите уравнение log₂ (x² − x + b) = log₂ (−3x + b) для всех значений действительного параметра b.

12. В треугольнике ABC медиана AM (MÎ(BC)) перпендикулярна медиане BN (NÎ(AC)). Найдите площадь треугольника, если AM = a, BN = b.

Решения

1. Поскольку геометрическим представлением комплексного числа z = a + bi является точка B(a;b), и B имеет координаты (−2;−3), следует, что z = −2 −3i.
Ответ: z = −2 −3i.

2. Уравнение f(x) = a, aÎR имеет три различных действительных корня при aÎ(−2;2), так как только при этих значениях параметра a прямая y = a пересекает график функции f(x) в трех различных точках.
Ответ: aÎ (−2;2).

3. Так как AB является диаметром, координаты середины этого отрезка являются координатами центра окружности. Используя формулы для вычисления координат (x₀; y₀) середины отрезка, соединяющего точки A(x₁; y₁) и B(x₂; y₂)

получим x₀ = 1 и y₀ = 4.
Применив формулу для нахождения расстояния между двумя данными точками A(x₁; y₁) и B(x₂; y₂),

вычислим длину диаметра AB:

Поскольку радиус окружности R равен половине диаметра, следует, что R =

. Уравнение окружности радиуса R с центром в точке O(x₀;y₀) имеет вид

(x − x₀)² + (y − y₀)² = R².

Подставляя x₀ = 1, y₀ = 4 и R =

, получим (x − 1)² + (y − 4)² = 8.
Ответ: (x − 1)² + (y − 4)² = 8.

4. Используем биномиальную схему (Бернулли):

p_n(k) = C_n^k p^k q^{n − k},

где n – число независимых испытаний;
k – число исходов, благоприятствующих событию A (0 ≤ k ≤ n);
p – вероятность реализации события A в каждом отдельном испытании (одинакова для всех испытаний);
q=1 − p;
p_n(k) – вероятность реализации события A ровно k раз в n независимых испытаниях.
Вероятность выпадения "орла" p в каждом из трех (n=3) подбрасываний (независимых испытаний) одинакова и равна ¹/₂. Следовательно,

Ответ: p₃(2) = ³/₈.

5. Применяя формулу для (k+1)-ого члена разложения бинома
T_k+1 = C_n^ka^n−k b^k, получим:

Поскольку девятый член не содержит x, то

, откуда n=20. Следовательно,

Ответ: A₂₀² = 380.

6. Заметим, что и, используя формулу Ньютона-Лейбница, получим:

Ответ:

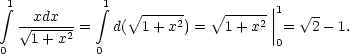
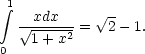
7. Так как 0 < sin2 < 1, функция (sin2)^x является убывающей. Следовательно,
(sin2)^x²−x ≥ sin² 2 Û x²−x ≤ 2 Û x²−x−2 ≤ 0 Û (x+1)(x−2) ≤ 0 Û −1 ≤ x ≤ 2.
Ответ: x Î [−1;2].

8. Пусть h – высота и d – диаметр основания цилиндра. Так как осевое сечение цилиндра представляет собой прямоугольник со сторонами h и d, имеем Q=dh. Поскольку площадь боковой поверхности цилиндра S_lat. = pdh и dh=Q, получим S_lat. = pQ.
Ответ: S_lat. = pQ.

9. Применив теорему Безу, получаем равенство P(2) = P(−1), то есть

8 + 8a − 10 − a − 9 = −1 + 2a + 5 − a − 9,

откуда a=1. Следовательно, P(X) = X ³ + 2X ² − 5X − 10. Корни многочлена P(X) найдем, решая уравнение P(X) = 0.
X ³ + 2X ² − 5X − 10 = 0 Û (X ³−5X) + (2X ²−10) = 0 Û X(X ²−5) + 2(X ²−5) = 0 Û
Û (X ²−5)(X+2) = 0 Û (X−5)(X+5)(X+2) = 0,
откуда X₁ =

, X₂ = −

, X₃ = −2.
Ответ: корнями многочлена P(X) являются −

, −2,

10. Уравнение касательной к графику функции f(x) в точке (x₀; f(x₀)) имеет вид

y = f '(x₀)(x−x₀) + f(x₀).

В данном случае

тогда уравнение касательной к графику функции f в точке M(3;2)

или

Найдем координаты вершин треугольника, образованного биссектрисами координатных углов (y=x и y=−x) и касательной к графику функции f, решая системы линейных уравнений:

Применив формулу для нахождения площади треугольника, вершинами которого являются A(x₁; y₁), B(x₂; y₂), C(x₃; y₃):

получим

Ответ: S = 5 (кв.ед.).

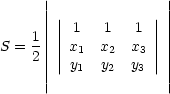
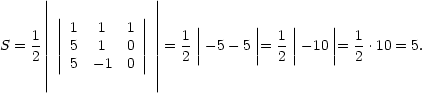
11. log₂(x²−x+b) = log₂(−3x+b) Û Û

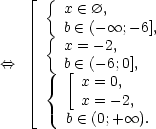
Ответ: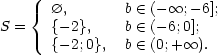

12.

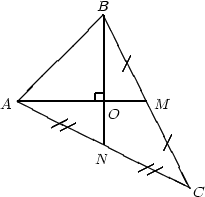
Пусть {AM}Ç{BN}={O}. Так как BN^AM и AO= a (медианы треугольника делятся точкой пересечения в отношении 2:1, считая от вершины),

S_ĎABN =

BN·AO =

b·

a =

Поскольку S_{Ď ABC} = 2S_ĎABN (свойство медианы), следует, что

S_ĎABC = 2 ·

(кв. ед.)

Ответ: S =

(кв. ед.)

Оценочная схема Максимальное число баллов
    N 1 – 3 балла
    N 2 – 3 балла
    N 3 – 3 балла
    N 4 – 4 балла
    N 5 – 5 баллов
    N 6 – 5 баллов
    N 7 – 5 баллов
    N 8 – 4 балла
    N 9 – 7 баллов
    N 10 – 8 баллов
    N 11 – 8 баллов
    N 12 – 6 баллов
    всего: 61 балл

Оценка
    "10" – 60-61 балл
    "9" – 55-59 баллов
    "8" – 48-54 балла
    "7" – 39-47 баллов
    "6" – 30-38 баллов
    "5" – 21-29 баллов
    "4" – 13-20 баллов
    "3" – 6-12 баллов
    "2" – 2-5 баллов
    "1" – 0-1 балл