Экзамен по математике на бакалавра, 2002, реальный профиль

Министерство образования Республики Молдова
Экзамен по математике на соискание звания бакалавра, 2002
Реальный профиль

Время работы: 180 минут.

1. Определите истинность высказывания "(") x Î R, x² + 9 – 6x > 0 ".

2. Вычислите

3. Постройте в одной системе координат графики функций f, g : [–3,3] ® R, для которых выполняются условия f(x) < g(x) и f '(x) > g'(x).

4. Найдите расстояние от центра окружности x² + y² + 6x + 10y – 135 = 0 до начала координат.

5. При каких действительных значениях x и y числа z₁ = x² + 4y – yi и будут сопряженными?

6. Решите уравнение

7. Найдите интервалы монотонности функции f : R ® R,

8. Отношение площади основания конуса к площади его осевого сечения равно p. Найдите угол наклона образующей к плоскости основания конуса.

9. Найдите корни многочлена P(X) = X ³ – 15X ² + 74X – 120, если известно, что один из его корней является средним арифметическим двух других корней.

10. Вокруг трапеции описана окружность. Боковая сторона трапеции образует с большим основанием угол a, а диагональ трапеции образует с этим основанием угол b. Найдите отношение площади круга, ограниченного данной окружностью, к площади трапеции.

11. Задана функция f : [0,2] ® R, f(x) = 2x – x². Найдите действительный параметр m, при котором прямая y = mx делит подграфик функции на две равновеликие части.

12. При каких действительных значениях параметра a уравнение a (2^x + 2^–x) = 5 имеет одно решение?

Решения

1. Утверждение является ложным. Заметим, что x² + 9 – 6x = (x–3)² и для x = 3 получим (x–3)² = 0, следовательно, $ x, x = 3 Î R при котором x² + 9 – 6x не будет строго больше нуля.

3. Например:

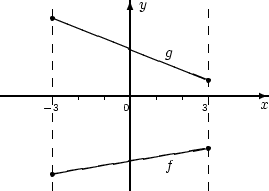
Действительно, поскольку g – строго убывающая функция, получим g'(x) < 0 и, так как f – строго возрастающая, f '(x) > 0, следовательно, g'(x) < f '(x) (xÎ [–3,3]).

4. Найдем каноническое уравнение окружности:
x² + y² + 6x + 10y – 135 = 0 Û (x² + 6x + 9) – 9 + (y² + 10y + 25) – 25 – 135 = 0 Û
Û (x+3)² + (y+5)² = 169.
Следовательно, координаты центра окружности O₁(–3; –5). Используя формулу расстояния между двумя данными точками, получим:

5.

Так как то следовательно, откуда y = 1 и x² = 1, то есть x = ± 1, y = 1.
Ответ: x = 1, y = 1 или x = –1, y = 1.

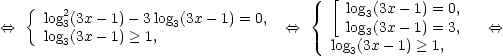
7. Найдем производную функции f :

Найдем критические точки функции f : f'(x) = 0 Þ x = 0 (заметим, что для " xÎ R $ f '(x)).
Определим знак производной и интервалы монотонности: для x < 0, f '(x) > 0 то есть при xÎ(– ¥,0] функция возрастает, для x > 0, f '(x) < 0, следовательно, при xÎ[0, + ¥) функция убывает.

8.

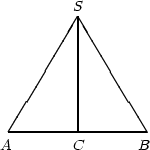
Пусть BC = AC = r – радиус конуса, SB = l – его образующая, SC = h – высота.
Поскольку площадь основания конуса равна , площадь осевого сечения и следует, что то есть r = h. Таким образом, прямоугольный треугольник SCB является равнобедренным и, значит, Ð SBC (угол между образующей и основанием конуса) равен 45^o.

9. Используя теорему Виета и условия задания, получим систему уравнений:

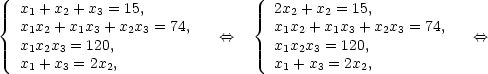
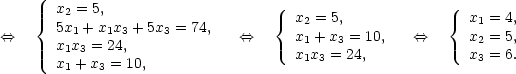
10.

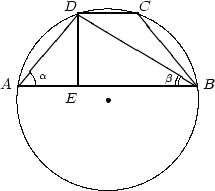
Так как около трапеции ABCD описана окружность, следует, что трапеция является равнобедренной. Следовательно, Ð DAB = Ð CBA = a, AC = BD. Тогда Ð DBC = a-b. Пусть радиус окружность равен R. По теореме синусов получим:

CD = 2Rsin(a - b)
AB = 2R sin(180^o – (a + b)) = 2Rsin(a + b).

Обозначим за DE = h высоту трапеции. Тогда

DE = BD sinb = 2Rsina × sinb

таким образом,

= 2R² sin²a × sin2b.

Следовательно,

11.

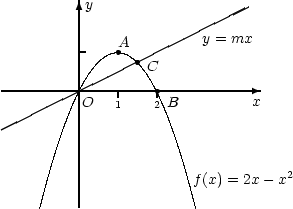
Найдем площадь подграфика функции f :

Найдем абсциссу точки C:

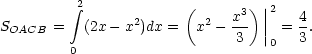
2x – x² = mx Þ x² + (m – 2)x = 0 Þ

é
ë

x₁ = 0,

x₂ = 2 – m.

Так как x₂ Î [0,2] Þ 0 ≤ 2 – m ≤ 2, откуда m Î [0,2].
Найдем площадь фигуры, ограниченной графиками функций f(x) = 2x – x² si y = mx:

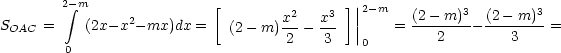
Поскольку

получим

откуда (2 – m)³ = 4, 2 – m =

, то есть, m = 2 –

. Заметим, что m = 2 –

Î [0,2], значит, удовлетворяет условиям задания.
Ответ: m = 2 –

12. Так как 2^x + 2^–x > 0, следует, что уравнение имеет решения только при a > 0. Тогда уравнение примет вид

2^x + 2^–x = ⁵/_a .

Поскольку функция f : R ® R, f(x) = 2^x + 2^–x является четной и строго возрастающей, последнее уравнение имеет единственное решение если и только если x = 0, откуда a = ⁵/₂.

Оценочная схема Максимальное число баллов
    N 1 – 2 балла
    N 2 – 4 балла
    N 3 – 4 балла
    N 4 – 4 балла
    N 5 – 5 баллов
    N 6 – 6 баллов
    N 7 – 5 баллов
    N 8 – 6 баллов
    N 9 – 7 баллов
    N 10 – 9 баллов
    N 11 – 10 баллов
    N 12 – 10 баллов
    всего: 72 балла

Оценка
    "10" – 69-72 балла
    "9" – 63-68 баллов
    "8" – 54-62 балла
    "7" – 42-53 балла
    "6" – 31-41 балл
    "5" – 23-30 баллов
    "4" – 15-22 балла
    "3" – 7-14 баллов
    "2" – 2-6 баллов
    "1" – 0-1 балл