Экзамен по математике на бакалавра, 1999, профиль: химия-биология

1. Пусть дана функция

Вычислить f(log₂3).

Решение.

Используя свойства логарифма, получим:

Таким образом, f(log₂3) = ³/₈.

2. Напишите уравнение второго порядка с действительными корнями, произведение которых равнялось бы 4.

Решение. Пусть x₁ = 1, x₂ = 4. Тогда x₁·x₂ = 1·4 = 4, x₁+x₂ = 5 и, используя обратную теорему Виета, получим квадратное уравнение

x² - 5x + 4 = 0.

3. Пара действительных чисел (x;y) удовлетворяет равенству x - i = yi. Определить действительные значения a, при которых данная пара удовлетворяет и равенству x - i² = 2a - y.

Решение. Имеем x - i = yi Ы x-i(y+1) = 0. Используя определение равенства двух комплексных чисел (Rez₁ = Rez₂ и Imz₁ = Imz₂), получим систему

	x = 0,
	y+1 = 0,

откуда x = 0 и y = -1.

Поскольку i² = -1,

x - i² = 2a - y Ы x + 1 = 2a - y, или, учитывая что x = 0 и y = -1, получим 1 = 2a + 1, откуда a = 0.

4. Какой член разложения бинома не содержит a?

Решение. Поскольку запишем бином в форме Используя формулу биноминального коэффициента

получим уравнение

или -8(17 - k) + 9k = 0, откуда k = 8.

Следовательно,

5. При каких значениях действительного параметра p функция f(x) = cos x - px + 2 монотонно возрастает на R.

Решение. f ў(x) = (cos x - px + 2)ў = -sin x - p. Функция f монотонно возрастает на R, если

-sin x - p ≥ 0 для "x О R.

Поскольку -1 ≤ sin x ≤ 1 для x О R, неравенство sin x ≤ -p имеет решения x О R, если и только если -p ≥ 1 или p ≤ -1.

6. В равнобедренной трапеции меньшее основание равно непараллельным сторонам и равно 16см, а диагональ перпендикулярна непараллельной стороне. Найти длину диагонали и площадь трапеции.

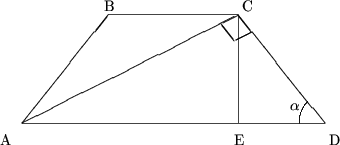
Решение. Пусть РCDA = РBCA = a (равнобедренная трапеция). Из прямоугольного треугольника ACD (AC^CD) следует РCAD = 90°-a и РCAD = РBCA (внутренние накрест лежащие углы). Поскольку AB = BC = 16 следует, что треугольник ABC - равнобедренный и РBAC = РBCA = 90°-a.

Таким образом, AC - биссектриса угла BAC и

a = 2(90°-a), откуда a = 60°. Из треугольника ACD получим AD = 2·CD = 2·16 = 32(см) (CD = 16(см) есть катет, противолежащий углу в 30°) и

(см).

Находим высоту CE трапеции:

или

(см). и площадь трапеции

(см²).

7. При каких действительных значениях параметра a справедливо равенство

2f ўўў(x) + 3f ўў(x) - 8f ў(x) + 3f (x) = 0, где f (x) = e^ax.

Решение. Определим первые три производные функции f :

f ў(x) = ae^ax, f ўў(x) = a²e^ax, f ўўў(x) = a³e^ax и получим уравнение 2a³e^ax + 3a²e^ax - 8ae^ax + 3e^ax = 0, или, поскольку e^ax ≠ 0, 2a³ + 3a² - 8a + 3 = 0. Удобно группируя, получим (2a³ + 6a²) - (3a² + 9a) + a + 3 = 0, 2a²(a + 3) - 3a(a + 3) + (a + 3) = 0, или (a + 3)(2a² - 3a + 1) = 0 откуда (a + 3)(a - 1)(2a - 1) = 0, и a = -3, a = 1, a = ¹/₂.

8. Определите первообразную функции график которой проходит через точку A(0;4).

Решение. Используя свойства неопределенного интеграла, получим

Определим значение постоянной C (F(0) = 4)

откуда C = 3. Таким образом,

9. Решить неравенства , где a - действительный параметр, a > 0.

Решение.

Ы		a - x < 0,
		2ax - x² ≥ 0,
		a - x ≥ 0,
		2ax - x² ≥ (a-x)².

Решая первую систему совокупности, получим

	a - x < 0,
	x(2a-x) ≥ 0

	x > a,
	0 ≤ x ≤ 2a

Ы x О (a;2a]

(здесь было использовано, что a > 0).

Решая вторую систему совокупности, получим

	a-x ≥ 0,
	2ax - x² ≥ a² - 2ax + x²

	x ≤ a,
	2x² - 4ax + a² ≤ 0

Таким образом, неравенство имеет решения

10. Величина угла между высотой правильной треугольной пирамиды и апофемой боковой грани равна 30°. Найти объем пирамиды, если длина апофемы равна 12см.

Решение. Пусть SO - высота пирамиды, SD - апофема (SD^BC). Тогда AD^BC и SO^AD Из прямоугольного треугольника SOD

(см). OD = SD sin 30° = 12· ¹/₂ = 6(см). Так как высота правильной треугольной пирамиды падает в точку пересечения биссектрис (в этом случае и медиан), OD = ¹/₃AD Ю AD = 18. Из прямоугольного треугольника ABD

(см). Следовательно, площадь основания пирамиды равна

(см²) и её объем

(см³).