Admiterea 2000, Test de evaluare la matematica

1. De rezolvat inecuatia

≥ 1

A) x Î	B) x Î [6;+¥)	C) x Î È [6;+¥)
D) x Î	E) x Î .

2. Cate radacini ale ecuatiei

2sinx·cosx - 3(sinx + cosx) + 3 = 0 apartin segmentului

. A) una B) nici una C) doua D) trei E) patru.

3. De rezolvat inecuatia

log_x²2 - 5log_x2 + 6 ≥ 0

A) x Î (0;1) È (1;+¥)	B) x Î (0,1) È (1;] È [;+¥)
C) x Î (0;1) È [;+¥)	D) x Î (1;] È [;+¥)
E) x Î (1;)

4. De gasit marimile unghiurilor intr-un triunghi, daca se stie ca inaltimea si mediana duse din acelasi varf al triunghiului impart unghiul respectiv in trei parti egale.

A) 30°, 30°, 120°	B) 45°, 45°, 90°	C) 30°, 60°, 90°
D) 60°, 60°, 60°	E) 25°, 55°, 100°.

5. Care dintre urmatoarele afirmatii sunt juste? (Pentru afirmatiile juste sa se utilizeze semnul de incercuire , iar pentru cele false ×)

Pentru orice triunghi ABC este adevatata relatia cosA + cosB + cosC ≤ ;
Daca un patrulater are centru de simetrie, atunci acest patrulater este un dreptunghi;
Intr-un tringhi isoscel centrul cercului inscris coincide cu centrul cercului circumscris acestui triunghi;
Intr-un trapez isoscel punctul de intersectie al diagonalelor este centru de simetrie al acestui trapez;
Intr-un triunghi dreptunghic centrul cercului circumscris coincide cu mijlocul ipotenuzei acestui triunghi.

Probe selectate de dr. S.Cataranciuc, conferentiar al USM.

Solutii

1. Inecuatia este echivalenta cu inecuatia

≥ 1 +

Cum ambii membri ai inecuatiei sunt pozitivi, ridicand la patrat, se obtine inecuatia echivalenta

4x + 1 ≥ 1 + 2

+ 2x + 4 sau, simplificand prin 2 si izoland radicalul, x - 2 ≥

Ultima inecuatie este echivalenta cu sistemul

	x - 2 ≥ 0,
	(x - 2)² ≥ 2x + 4,
	2x + 4 ≥ 0.

Se rezolva sistemul de inecuatii

	x ≥ 2,
	x² - 4x + 4 ≥ 2x + 4,
	x ≥ -2,

	x ≥ 2,
	x(x - 6) ≥ 0,

x ≥ 2,

	x ≤ 0,
	x ≥ 6,

si se obtine x ≥ 6.

Prin urmare, multimea solutiilor inecuatiei este [6;+¥).

Raspuns: B.

2. Se noteaza sinx + cosx = t, (|t| ≤ ), atunci , si ecuatia devine

t² - 1 - 3t + 3 = 0 sau t² - 3t + 2 = 0, de unde t₁ = 1 si t₂ = 2 (nu verifica conditia |t| ≤

). Asadar sinx + cosx = 1.

Se utilizeaza metoda unghiului auxiliar (a se vedea Ecuatii trigonometrice) si se obtine

Cum x Î , rezulta x₁ = 0 si x₂ = si, prin urmare, pe segmentul dat ecuatia are doua solutii.

Raspuns: C.

3. DVA al inecuatiei este multimea x Î (0,1) È (1,+¥). Se noteaza log_x2 = t si se obtine inecuatia patratica t² - 5t + 6 ≥ 0 cu solutiile t ≤ 2 sau t ≥ 3. Asadar

Raspuns: B.

4. Fie in triunghiul ABC BD^AC (inaltime), BE - mediana (AE = EC = a) ÐABD = ÐDBE = ÐEBC = a.

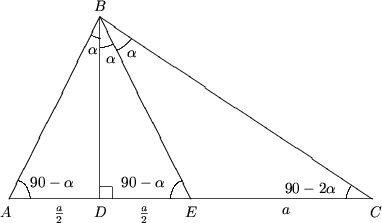
Cum BD inaltime si bisectoare, DABE este isoscel si, prin urmare, BD - mediana,

Din DABD: Se utilizeaza teorema sinusurilor:

de unde 4sinacos2a = sin3a, sau 4sina(1 - 2sin²a) = sina(3 - 4sin²a).

Cum a ≠ pk, k Î Z, rezulta

4 - 8sin²a = 3 - 4sin²a, sau 4sin²a = 1 de unde sina = ¹/₂ (sina = -¹/₂ nu verifica conditiile problemei) si a = 30°. Asadar unghiurile triunghiului sunt ÐABC = 3a = 90°, ÐBAC = 90 - a = 60°, ÐBCA = 30°.

Raspuns: C.

Afirmatie justa. Cum (R (r) - raza cercului circumscris (inscris) in triunghi), iar 2r ≤ R, rezulta
Afirmatie falsa. De exemplu, rombul are centru de simetrie, dar nu numaidecat este dreptunghi.
Afirmatie falsa. De exemplu, intr-un triunghi isoscel dreptunghic centrul cercului circumscris coincide cu mijlocul ipotenuzei, iar centrul cercului inscris se afla in interiorul triunghiului.
Afirmatie falsa. Rezulta din definitia centrului de simetrie.
Afirmatie justa. Rezulta din teorema sinusurilor 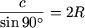Þ c = 2R si (c - ipotenuza, R - raza cercului circumscris).

Raspuns: a. si e. sunt afirmatii juste.