Examenul de absolvire a scolii medii de cultura generala, clasa a XI-a, 13 iunie 2008

Ministerul Educatiei si Tineretului al Republicii Moldova
Agentia de Evaluare si Examinare
Matematica
Examenul de absolvire a scolii medii de cultura generala, clasa a XI-a, 13 iunie 2008

Timp alocat: 180 minute.

In itemii 1-4 completati spatiile rezervate astfel incat propozitiile obtinute sa fie adevarate.

1. Ordonati crescator numerele
Raspuns: ; ; .

2. In desen ABCD este un dreptunghi. AB = BM, M ∈ (BC). m(∠AMC) = .

3. Incercuiti litera A, daca propozitia este adevarata, sau litera F, daca propozitia este falsa.

"|x| > x pentru orice x ∈ R".

4. Completati caseta astfel incat propozitia obtinuta sa fie adevarata.

Daca 3^x − 3^y = 0, x, y ∈ R, atunici 3^x−y =

5. La orele 15:00 stalp cu inaltimea de 3 m are lungimea umbrei egala cu 4,2 m. Determinati inaltimea unui copac, daca se stie ca lungimea umbrei lui la orele 15:00 este de 7,7 m.

6. Calculati sin2α, daca se stie ca sinα + cosα = 0,8.

7. In luna februarie salariul unui muncitor a fost majorat cu 20 % fata de salariul lui din luna ianuarie, iar in martie — a fost majorat cu 10 % fata de luna februarie. Cu cate procente a fost majorat salariul muncitorului in luna martie fata de salariul din luna ianuarie?

8. Scrieti ecuatia tangentei la graficul functiei f: R → R, in punctul x₀ = −1.

9. Rezolvati in R inecuatia

10. Determinati volumul piramidei patrulaterale regulate, daca se stie ca lungimea muchiei laterale este egala cu lungimea diagonalei bazei si este egala cu 6 cm.

11. Rezolvati in R ecuatia log ₃(3^4x − 3^2x+1 + 3) = 2log ₉7.

12. Determinati functia de gradul al doilea, f: R → R, care verifica conditiile: f '(1) = 3;
f(2) + f '(2) = 12 si

Solutii

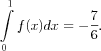
1. Prin urmare,

Raspuns:

2. Cum ΔABM — dreptunghic isoscel, rezulta ∠BMA = 45^o si ∠AMC = 180^o − 45^o = 135^o.
Raspuns: 135^o.

3. Fals, deoarece |x| > x are loc pentru orice x ∈ R_{_}^*, si nu pentru ∀x ∈ R.

4. Cum 3^x − 3^y = 0 ⇒ 3^x = 3^y ⇒ x = y, rezulta

3^{x − y} = 3^{x − x} = 3⁰ = 1. Raspuns: 1.

5.
Avem: BC = 3, AC = 4,2 si AD = 7,7. Cum triunghiurile ADE si BCA sunt asemenea, se obtine:

de unde

Raspuns: 5,5 m.

6. sinα + cosα = 0,8 ⇒ (sinα + cosα)² = 0,8² ⇒ sin²α + 2 sinαcosα + cos²α = 0,64 ⇒
⇒ 1 + sin2α = 0,64 ⇒ sin2α = −0,36.
Raspuns: −0,36.

7. Fie salariul din una ianuarie x lei. Atunci salariul din luna februarie iar salariul din luna martie Alcatuim proportia:

x — 100 %,
1,32x — z %, de unde z = 132 %. Asadar, salariul a fost majorat cu 132 % − 100 % = 32 %.
Raspuns: cu 32 %.

8. Ecuatia tangentei la graficul functiei f '(x) in punctul x₀:

y − f(x₀) = f '(x₀)(x − x₀).
Aflam:
a)

d) ecuatia tangentei: y + 2 = −2(x − 1),
y = −2x + 2 − 2,
y = −2x. Raspuns: y = −2x.

9.
⇔ x ∈ [−2; −1] ∪ {2}.
Raspuns: x ∈ [−2; −1] ∪ {2}.

10.

Consideram ΔMBD: MO = h, MB = MD = 6 (cm), MD = DB = 6 (cm). Rezulta ΔMBD — echilateral.

Consideram ΔADB dreptunghic in A. AD = AB, deci, triunghiul este isoscel.

Rezulta

(cm²).
Aflam volumul piramidei:

Raspuns: V = 18

(cm³).

11. log ₃(3^4x − 3^2x+1 + 3) = 2log ₉7 ⇔ log ₃(3^4x − 3⋅3^2x + 3) = log ₃7 ⇔
⇔ 3^4x − 3⋅3^2x + 3 = 7 ⇔ 3^4x − 3⋅3^2x − 4 = 0.
Notam 3^2x = t, t > 0 si ecuatia devine

t² − 3t − 4 = 0 cu solutiile t₁ = −1 (nu verifica conditia t > 0) si t₂ = 4. Asadar, 3^2x = 4 ⇔ 2x = log₃4 ⇔ 2x = 2 log₃2 ⇔ x = log₃2. Raspuns: x = log₃2.

12. Fie f(x) = ax² + bx + c. Cum f '(x) = 2ax + b si f '(1) = 3, avem 2a + b = 3.
Cum f(2) + f '(2) = 12, iar f '(2) = 4a + b, avem

4a + 2b + c + 4a + b = 12 sau 8a + 3b + c = 12. Cum

avem

sau 2a + 3b + 6c = −7. Se obtine sistemul:

Asadar,

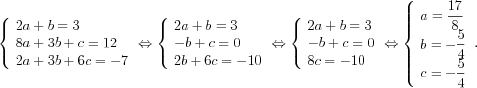
Raspuns:

Schema de notare Scor maxim
    Nr. 1 — 3 puncte
    Nr. 2 — 2 puncte
    Nr. 3 — 2 puncte
    Nr. 4 — 2 puncte
    Nr. 5 — 4 puncte
    Nr. 6 — 4 puncte
    Nr. 7 — 5 puncte
    Nr. 8 — 5 puncte
    Nr. 9 — 8 puncte
    Nr. 10 — 5 puncte
    Nr. 11 — 7 puncte
    Nr. 12 — 9 puncte
    total: 56 puncte