| Pagina principala | Ghidul utilizatorului | Rubrica candidatului | Curriculumurile scolare |
| Matematica competitiva | Matematica distractiva| Formule, dictionare | Avizuri |
|Pagini din istorie | Examene, teste | Bibliografie | Link-uri | Site map |

Ministerul Educatiei si Stiintei
Examenul de bacalaureat la matematica, sesiunea iunie, 1999
Profilul umanist
Varianta I

Timp de realizare - 180 minute

1. Fie functia f:R*®R, Calculati f(log32).

Solutie. Se tine seama de identitatea logaritmica de baza a > 0, a ¹ 1, b > 0 si se obtine

2. Dati exemplu de ecuatie de gradul doi care admite radacinile reale negative distincte.

Solutie. Se utilizeaza teorema reciproca a lui Viete de exemplu, pentru x1 = -1 si x2 = -2, si se obtine ecuatia patrata x2+3x+2 = 0. In caz general, o ecuatie patrata ax2+bx+c = 0 are doua solutii reale negative distincte daca si numai daca:

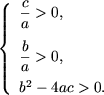
3. Pentru care valori reale ale lui x si y este adevarata egalitatea

Solutie. Egalitatea se scrie

x + y + (y - 3)i = (1 + i)(5 + 3i)
sau
x + y + (y - 3)i = 2 + 8i,
de unde, tinand seama de definitia egalitatii a doua numere complexe z1 si z2 (Rez1 = Rez2 si Imz1 = Imz2), se obtine sistemul
x + y = 2,
y - 3 = 8
cu solutiile x1 = -9 si y = 11.

4. Rezolvati ecuatia .

Solutie.

Û
x - 4 = 0,
3 + 2x - x2 = 0,
3 + 2x - x2 ³ 0,
 Û
x1 = 4,
x2 = -1,   x3 = 3,
-1 £ x £ 3,
 Û
x1 = -1,
x2 = 3.

5. Fie functia f(x) = asin4x + bcos2x. Sa se determine parametrii reali a si b, daca se stie ca si .

Solutie. Se determina derivata functiei f(x):

f ¢(x) = (asin4x + bcos2x)¢ = 4acos4x - 2bsin2x.
Cum si , rezulta
sau
2a + b = 4,
-4a + 2b = 2,
de unde a = 3/4  si   b = 5/2.

6. Sa se calculeze aria multimii marginite de graficele functiilor f(x) = 9 - x2 si g(x) = x2 - 6x + 9.

Solutie.

Aria figurii marginite de graficele functiilor f(x) = 9-x2 si g(x) = x2-6x+9 (a se vedea desenul) se determina din formula

unde a si b sunt limitele de integrare, ce se obtin rezolvand ecuatia
f(x) = g(x),
adica 9 - x2 = x2 - 6x + 9 sau 2x2 - 6x = 0, de unde (tinand seama ca a < b) se obtine a = x1 = 0 si b = x2 = 3.

Asadar

7. Daca impartim polinomul P(x) = 2x3 - mx2 + nx-16 la x - 3 si la x + 1, obtinem in ambele cazuri restul -2. Ce rest vom obtine, daca vom imparti polinomul P(x) la x-1.

Solutie. Cum

P(3) = 2·33 - m·32 + 1·3 - 16 = -2,
P(-1) = 2(-1)3 - m·(-1)2 + n·(-1) - 16 = -2,
rezulta
-9m + 3n = -40,
-m - n = 16.
Rezolvand sistemul, se obtine m = -2/3 si n = -46/3. Asadar polinomul P(x) devine si restul la impartirea lui la (x - 1) este egal cu

8. Aria bazei unui con circular drept este 9pcm2, iar aria suprafetei totale este 24pcm2. Aflati volumul conului circular drept.

Solutie.

Cum aria bazei Sb = pR2 (R - raza bazei conului), aria suprafetei totale Slat = pRl (l - generatoarea conului), se obtine sistemul:

pR2 = 9p,
pRl = 24p - 9p,
de unde, R = 3 si l = 5. Din triunghiul dreptunghic SOA (a se vedea desenul), se determina inaltimea conului SO:
Prin urmare, volumul conului

9. Rezolvati inecuatia log2x(x2 - 5x + 6) £ 1.

Solutie.

log2x(x2 - 5x + 6) £ 1   Û   log2x(x2 - 5x + 6) £ log2x2x   Û
Û  
2x > 1,
x2 - 5x + 6 £ 2x,
x2 - 5x + 6 > 0,
0 < 2x < 1,
x2 - 5x + 6 ³ 2x,
2x > 0,
 Û
x > 1/2,
x2 - 7x + 6 £ 0,
x < 2,
x > 3,
0 < x < 1/2,
x2 - 7x + 6 ³ 0,
x > 0,
   Û  
1/2 < x < 2,
x > 3,
1 £ x £ 6,
0 < x < 1/2
x £ 1,
x ³ 6,
   Û
Û  
x Î (1/2;1]È(3;6],
x Î (0;1/2),
  Û   x Î (0;1/2)È(1/2;1]È(3;6].



| Pagina principala | Ghidul utilizatorului | Rubrica candidatului | Curriculumurile scolare |
| Matematica competitiva | Matematica distractiva| Formule, dictionare | Avizuri |
|Pagini din istorie | Examene, teste | Bibliografie | Link-uri | Site map |