Bacalaureat 1999, Profilul real

1. Sa se calculeze

(3 puncte)

Solutie. Nedeterminare de tipul Ľ-Ľ. Se aduce la numitor comun si se obtine

2. Dati exemplu de o functie definita si continue pe un interval deschis (a,b) dar care nu este marginita pe acest interval. (3 puncte)

Solutie.

In adevar,

3. Fie z = 1 + i. Sa se determine numerele reale a,b Î R, daca se stie ca z³ = az + b. (4 puncte)

Solutie. Se utilizeaza definitia egalitatii a doua numere complexe si se obtine:

(1 + i)³ = az + b Ű 1 + 3i + 3i² + i³ = a(1 + i) + b Ű 1 + 3i - 3 - i = a + b + ai Ű

Ű -2 - 2i = (a + b) + ai Ű

a+b = -2,

a = 2,

b = -4.

4. Calculati integrala

(5 puncte)

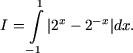
Solutie. Se tine seama ca integrantul reprezinta o functie para, deci 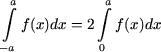si cum pentru x Î [0,1]: avem 2^x - 2^-x ł 0 se obtine:

5. Rezolvati ecuatia

3+4|cosx| = bcos2x, daca una din radacinile ei este

. (6 puncte)

Solutie. Cum x = verifica ecuatia, rezulta

Inlocuind valoarea lui b in ecuatia initiala se obtine 3 + 4|cosx| = -10 cos2x Ű 10(2cos² x - 1) + 4|cosx| + 3 = 0. Se efectueaza substitutia t = |cosx|, atunci cos²x = t² si tinand seama ca 0 Ł t Ł 1 se obtine ecuatia patrata 20t² + 4t - 7 = 0 cu solutiile t₁ = ¹/₂, t₂ = ^-7/₁₀. Cum t Î [0,1], ramane t = ¹/₂. Astfel:

6. Inaltimea unui con circular drept este egala cu 6cm, iar generatoarea conului formeaza cu planul bazei un unghi de 60^°. In con este asezata o piramida baza careia este un triughi dreptunghic isoscel inscris in baza conului, iar varful piramidei este mijlocul unei generatoare a conului. Aflati volumul piramidei. (5 puncte)

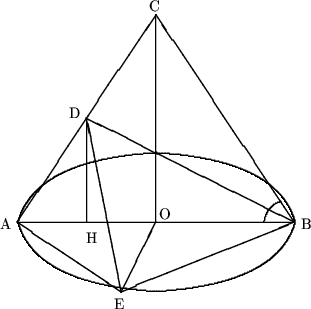
Solutie. Se considera triunghiul dreptunghic COB (CO^OB). Cum ĐCBO = 60^° (din enunt), si utilizand relatiile metrice in triunghi se obtine: Astfel ipotenuza triunghiului dreptunghic AEB, AB fiind si diametrul cercului de raza OB, este egala , iar aria AEB (aria bazei piramidei)

Inaltimea piramidei DH este linia mijlocie in triunghiul AOC, deci este egala cu o doime din OC,

Astfel,

7. Dreapta x + y - 4 = 0 este tangenta la elipsa

unde b Î (0,3). Sa se determine valoarea parametrului real b si coordonatele punctului de tangenta. (6 puncte)

Solutie. Ecuatia tangentei la elipsa in punctul (x₀,y₀) este

sau, in cazul dat,

de unde

Din enunt (y = -x + 4) rezulta:

de unde se obtine x₀ = ⁹/₄. Cum y₀ = 4 - x₀ Ţ y₀ = ⁷/₄, si utilizand ecuatia elipsei se determina b:

de unde 9b² + 49 = 16b² sau b² = 7,

si cum b Î (0,3), ramane

. Asadar

, si punctul de tangenta M(⁹/₄,⁷/₄).

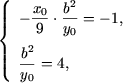
8. Sa se determine termenul care il contine pe b² din dezvoltarea binomului , stiind ca n este cel mai mare numar natural ce verifica inegalitatea

(7 puncte)

Solutie. Scriem inecuatia in n sub forma

Notam log₃n = t si obtinem

Tinand seama ca t > 0 din ultima inecuatie avem 1 < log₃x < 2 Ű 3 < n < 9. Cum n Î N si cel mai mare din intevalul (3;9), rezulta n = 8. Conform formulei lui Newton (binominale)

de unde ^k/₃ = 2 sau k = 6. Asadar

9. Se considera functia

f:DŽ R, D Ě R astfel incat

Sa se determine a, b astfel incat valorile in punctele de extrem sunt egale cu -1 si -2. (8 puncte)

Solutie. Se determina punctele critice:

Asadar f ˘(x) = 0 Ţ b² - x² = 0 Ţ x = ąb.

Se observa ca a š 0, b š 0 (altfel se incalca conditiile problemei) si in vecinatatile punctelor x = ąb derivata isi schimba semnul, prin urmare x = -b si x = b sunt puncte de extrem.

Se obtine urmatoarea totalitate de sisteme:

		f(b) = -1,
		f(-b) = -2,
		f(b) = -2,
		f(-b) = -1

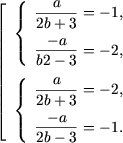
Din primul sistem se obtine a = -4, b = ¹/₂, iar din al doilea a = -4, b = -¹/₂, in ambele cazuri functia f fiind

10. Fie triunghiul dreptunghic ABC cu ĐC = 90^°. Mediana CP este perpendiculara pe mediana BQ si latura BC este a. Calculati lungimea medianei BQ. (8 puncte)

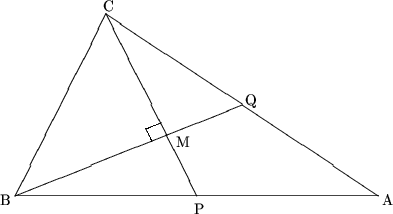
Solutie. Fie ĐCBA = a. Atunci ĐBAC = 90^°-a. Cum CP =¹/₂AB = BP = PA, rezulta ĐBCP = a si ĐACP = 90^°-a. Din triunghiul dreptunghic CMQ se obtine ĐCQB = a. Asadar triunghiul CBQ este asemenea cu triunghiul ABC de unde

Cum CQ = ¹/₂AC (BQ-mediana) rezulta

de unde

Utilizand teorema lui Pitagora se obtine AB² = a² + 2a² sau

Asadar