Agentia de Evaluare si Examinare
Examenul de bacalaureat la matematica, 14 iunie 2007
Profilul real
I. In itemii 1-4 scrie pe foaia de test in spatiul indicat numai rezultatele. Poti folosi maculatorul pentru efectuari de calcule.
1. Numarul 
este egal cu 
.
2. Daca A (x0, y0) este centrul cercului de ecuatie
x2 − 2x + y2 + 4y = 0, atunci
x0 = si
y0 = .
3. Timpul in care 30 de elevi au rezolvat o problema este prezentat in tabelul de mai jos:
| Timpul xi (min) | 15 | 5 | 11 | 6 | 16 | 9 | 12 | 7 | 13 | 8 |
| Nr. elevilor – ni | 3 | 1 | 5 | 2 | 1 | 3 | 4 | 2 | 6 | 3 |
.
4. Ecuatia asimptotei orizontale la +∞ a
graficului functiei f: R → R,
este
.
II. In itemii 5-8 raspunde la intrebari, scriind argumentarile si raspunsurile in spatiile rezervate.
5. Determina primitiva functiei f:
→ R, f(x) = tg x, graficul careia
contine punctul
.
6. Determina pentru care valori reale ale parametrului m
sistemul de ecuatii
este compatibil determinat.
7. In interiorul unui unghi XOY de 60o se gaseste un
punct M, care se afla la o distanta de 10 cm, respectiv 4 cm de
laturile OX, OY ale unghiului. Determina distanta de la punctul
M la varful O.
8. Determina cea mai mica solutie a ecuatiei 3lg x4 − 4⋅3lg x2 + 3 = 0.
III. Rezolva problemele 9-12 si scrie pe foaia de test rezolvarile complete.
9. Determina pentru cate valori intregi ale lui a numarul (a + i)4 este intreg.
10. In desenul alaturat EABC este o piramida
triunghiulara regulata, muchia laterala a careia formeaza cu planul
bazei un unghi de 60o. Determina raza sferei inscrise in aceasta
piramida, daca muchia laterala a piramidei este egala cu
a (in desen O1 este centrul sferei inscrise,
O1M = O1O –
raza sferei inscrise).
11. Determina toate valorile reale ale lui a, pentru care
tangenta la graficul functiei f: R →
R,
f(x) = x2 − 2x + 2 in punctul de abscisa x0 = a
intersecteaza axa absciselor in unul din punctele intervalului [0, 1].
12. In desenul alaturat AB reprezinta o cale ferata, iar
C un punct care se afla la distanta de 8 km de la aceasta cale
ferata si la distanta de 
km de la punctul A. Pentru
a transporta marfa din punctul A in punctul C se intentioneaza
sa se construiasca o sosea (rectilinie) din punctul C pana la un punct M al caii ferate. Se stie ca pretul pentru transportarea
unei tone de marfa pe calea ferata este de 30 de lei (pentru un kilometru), iar pe sosea de 50 de lei (pentru un kilometru).
Determina care trebuie sa fie distanta AM, astfel incat pretul
pentru transportarea unei tone de marfa din A in C (pe calea AMC) sa fie minim.
1. =
log3 9lg 10−1 + (−1) =
log3 9−1 − 1 =
log3 3−2 − 1 = −2 − 1 = −3.
2. Cum x2 − 2x + y2 + 4y = 0 ⇔
(x2 − 2x + 1) − 1 + (y2 − 4y + 4) − 4 = 0 ⇔
⇔ (x − 1)2 + (y − 2)2 = 5
si ecuatia cercului de raza R cu centrul in O (x0, y0) este
(x − x0)2 + (y − y0)2 = R2,
rezulta x0 = 1 si y0 = −2.
3. Aranjam seria statistica crescator, tinand seama de frecventele termenilor:
).
4. Dreapta y = b este asimptota orizontala la graficul
functiei f(x) cand x → +∞, daca
. Cum
,
.
5. Cum
Deoarece
,
cos x > 0 si |cos x| = cos x, prin urmare,
F(x) = − ln cos x. Cum graficul primitivei
contine punctul A se obtine
,
5 + ln 2 = C + ln 2,
de unde C = 5.
Raspuns: F(x) = ln cosx + 5.
6. Conform regulei Cramer, sistemul este compatibil
determinat, daca determinantul principal este diferit de zero. Cum
Δ =
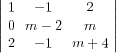= (m − 2)(m + 4) − 2m − 4(m − 2) + m =
= m2 + 2m − 8 − 2m − 4m + 8 + m
= m2 − 3m,
din conditia
m2 − 3m ≠ 0
se obtine
m ∈ R \ {0; 3}.
7. Fie MA⊥OX, MB⊥OY, A∈OX, B∈OY,
MA = 10 (cm), MB = 4 (cm). Prelungim AM pana la intersectie cu
OY, C – punctul de intersectie.
m(∠COA) = 60o, m(∠CAO) = 90o, rezulta
m(∠OCA) = 30o si CM = 2BM = 8 cm (cateta opusa unghiului de 30o).
Din ΔOAC avem
OA = ACtg 30o =
(cm); iar din
ΔOMA, conform teoremei Pitagora:
(cm).
8. DVA: x ∈ R\{0}. In DVA:
3lg x4 − 4⋅3lg x2 + 3 = 0
⇔
32lg x2 − 4⋅3lg x2 + 3 = 0
⇔
.
Toate solutiile sunt din DVA, prin urmare, multimea solutiilor
S = {−
, −1, 1, }
si cea mai mica solutie din S este x = −.
9. Utilizand formula binomului Newton, se obtine
z = a4 + 4a3i + 6a2i2 + 4ai3 + 1
= a4 + 4a3i − 6a2 − 4ai + 1
= (a4 − 6a2 + 1) + (4a3 − 4a)i.
Cum z ∈ Z, rezulta Im z = 0, adica 4a3 − 4a = 0, de unde
a ∈ {0; −1; 1}. Cum cardinalul acestei multimi este 3 si pentru
fiecare a din aceasta multime a4 − 6a2 + 1 ∈ Z, obtinem
raspunsul 3.
10. Deoarece piramida este regulata, rezulta ca inaltimea
EO se proiecteaza in centrul cercului circumscris bazei.
In ΔEOA dreptunghic OA = R = 
(cateta opusa unghilui de 30o). Conform teoremei Pitagora
r = O1O = MO1.
Din ΔEOD ∼ ΔEMO1 rezulta:
(*).
;
EO1 = EO − O1O = 
− r.
Din ΔEOD
dreptunghic, conform teoremei Pitagora, obtinem:
11. Ecuatia tangentei la graficul functiei f(x) in punctul (x0, f(x0)) este
,
a ∈ R \{1} (daca a = 1, ecuatia tangentei devine
y = 1 si nu intersecteaza axa OX).
Cum x∈[0, 1] se obtine sistemul de inecuatii
12.
Coboram CD⊥AB, D∈[AB]. Conform enuntului
AC = , CD = 8.
Fie AM = x, MC = y. Atunci pretul pentru
transportarea unei tone va fi C = 30x + 50y.
Din triunghiul dreptunghic ADC determinam AD:
.
.
Din C' = 0 rezulta
Verificam punctul x = 64 la extrema (semnul derivatei):
asadar, x = 64 este punct de minim, astfel distanta AM = 64 (km).
Nr. 1 – 2 puncte
Nr. 2 – 2 puncte
Nr. 3 – 2 puncte
Nr. 4 – 3 puncte
Nr. 5 – 4 puncte
Nr. 6 – 4 puncte
Nr. 7 – 5 puncte
Nr. 8 – 5 puncte
Nr. 9 – 6 puncte
Nr. 10 – 6 puncte
Nr. 11 – 7 puncte
Nr. 12 – 8 puncte
total: 54 puncte