Directia Invatamant Preuniversitar
Examenul de bacalaureat la matematica, iunie 2004
Profilul real
1. Functia f: [-4;4] ® R
este reprezentata grafic. Care propozitie este adevarata?
a) f '(0)=0 b) f '(0)>0 c) f '(0)<0 d) f '(0) nu exista.
2. Dreapta definita de ecuatia ax + by = 1 este paralela cu axa absciselor daca
a) a=0 si b=0 b) a=0 si b¹0
c) a¹0 si b=0 d) a¹0 si b¹0.
3. Care ecuatie admite o singura solutie pe intervalul (0; 2p]?
a) tgx = 1 b) cosx = 0 c) ctgx = −3 d) sinx = 1.
4. Completati caseta libera cu unul dintre semnele <, =, >, astfel incat propozitia sa fie adevarata.
0.
5. Calculati limita 
.
6. Determinati termenul din mujloc al dezvoltarii binomului 
.
7. Rezolvati in R inecuatia D(x) £ 0, unde 
.
8. Baza unei piramide triunghiulare este triunghiul dreptunghic ABC, unde
m(Ð A) = 90o,
m(Ð B) = 60o,
|AC| = 
cm. Determinati volumul piramidei,
daca muchiile laterale sunt congruente si au lungimea egala cu 13 cm.
9. Determinati extremele locale ale functiei f: R ® R, f(x) = x× e1−2x2.
10. Rezolvati in R ecuatia log3x2 − log32(−x) + 3 = 0.
11. Unul dintre zerourile unei primitive a functiei f: R ® R, f(x) = x2 − 4x + 1 este egal cu 2. Determinati celelalte zerouri ale acestei primitive.
12. Intr-un trapez isoscel bazele au lungimi egale cu 21 cm si 9 cm, iar lungimea inaltimii este egala cu 8 cm. Determinati raza cercului circumscris acestui trapez.
13. Fie polinomul P(X) = X 4 − X 3 − aX 2 + (b−2)X + a, unde a, bÎ R. Se stie ca a = 1 + i este radacina a polinomului P(X). Determinati valorile parametrilor reali a si b.
14. Rezolvati in R inecuatia 
.
1. Raspuns corect b) f '(0)>0.
2. Raspuns corect b) a=0 si b¹0.
3. Raspuns corect d) sinx = 1.
4. lg tg 40o + lg ctg 40o = lg (tg 40o × ctg 40o) = lg1 = 0.
5. 
Raspuns: 72.
6. Cum n=6, dezvoltarea binomului contine 7 termeni si termenul din mijloc este T4.
Raspuns: $T_4=20$.
7. Descompunem determinantul dupa linia a 4 si obtinem:
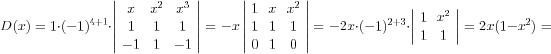
= 2x(1−x)(1+x).
Utilizand metoda intervalelor, pentru inecuatia D(x)£0
Û
2x(1−x)(1+x)£0, se obtine
Raspuns: xÎ[−1;0]È[1;+¥).
8. 
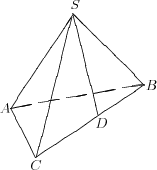
Cum muchiile laterale sunt congruente, piciorul D al inaltimii SD=h se afla in mijlocul ipotenuzei BC.
Determinam ipotenuza BC:
. Din
DSDB (dreptunghic in D) aflam inaltimea piramidei h:
cm3.
9. Aflam derivata functiei f:
f '(x) = x'e1−2x2 + xe1−2x2(1−2x2)' =
e1−2x2 + xe1−2x2(−4x) =
e1−2x2(1−4x2).
Aflam punctele critice, rezolvand ecuatia f '(x) = 0:
f '(x) = 0 Û
e1−2x2(1−4x2) = 0
Û
x1= −
si
x2= .
Determinam semnul functiei f ' pe intervale
si
si obtinem extremele locale:
x = − punct de minim,
si
.
Raspuns: fmin = −
,
fmax = .
10. DVA: x<0.
log3x2 − log32(−x) + 3 = 0
Û
2log3|x| − log32(−x) + 3 = 0
Û
Raspuns: x Î {−
; −27}.
11. F(x) = 
=
− 2x2 + x + C.
Cum F(2)=0, rezulta: 
− 8 + 2 + C = 0,
de unde
C = 
.
Prin urmare,
F(x) = − 2x2 + x +
. Determinam, celelalte radacini:
F(x)=0
Û
x3 − 6x2 + 3x + 10 = 0
Û
x3 − 2x2 − 4x2 + 8x − 5x + 10 = 0
Û
Û
x2(x−2) − 4x(x−2) − 5(x−2) = 0
Û
(x−2)(x2−4x−5) = 0
Û
(x−2)(x+1)(x−5) = 0,
de unde x2 = −1, x3 = 5.
Raspuns: x2 = −1, x3 = 5.
12. 
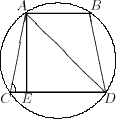
Fie AB = 9 cm, CD = 21 cm, AE^DC, AE = 8 cm.
Cum trapezul ABCD este isoscel
(cm), atunci
(cm) (din D AED
dreptuinghic in E). Din D AEC (dreptunghic in E) aflam AC:
(cm). Atunci
, de unde
Raspuns: R =
cm.
13. Cum a = 1 + i radacina a polinomului P(X), rezulta
P(a) = 0 si
(1+i)4 − (1+i)3 − a(1+i)2 + (b−2)(1+i) + a = 0
Û
Û
1 + 4i3 + 6i2 + 4i3 + i4 − 1 − 3i − 3i2 − i3 − a(1+2i+i2) + (b−2) + i(b−2) + a = 0
Û
Û
1 + 4i − 6 − 4i + 1 − 1 − 3i + 3 + i − 2ai + (b−2) + i(b−2) + a = 0
Û
Û
a − 2 + b − 2 + i(b−2−2−2a) = 0
Û
a + b − 4 + i(b−2a−4) = 0.
Utilizand definitia egalitatii a doua numere complexe, obtinem
de unde
Raspuns: a = 0, b = 4.
14.
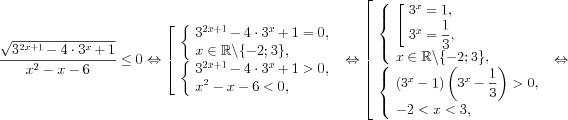
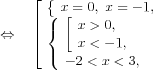Û
xÎ(−2;−1]È[0;3).
Raspuns: xÎ(−2;−1]È[0;3).