Bacalaureat 2001, Profilul real

Ministerul Educatiei si Stiintei
Examenul de bacalaureat la matematica, 2001
Profilul real

Timp alocat: 180 minute.

1. Intre care numere intregi consecutive se afla numarul ?

2. Dati exemplu de o functie care nu este definita in punctul de abcisa x = 3, dar are limita finita in acest punct.

3. Determinanti termenul al patrulea al dezvoltarii binomului .

4. Cercurile de ecuatii x² + y² = -4x si x² + y² = 4y au o coarda comuna. Scrieti ecuatia dreptei ce contine aceasta coarda.

5. Fie polinomul P(x) = x³ - 2x² - 7x - 3. Calculati restul impartirii plinomului P(x) la binomul x - a, daca a = 3 - i.

6. Rezolvati inecuatia .

7. Calculati volumul corpului de rotatie determinat de functia f(x) = -x² + 4x, daca x Î [0;2].

8. Determinati raza cercului circumscris triunghiului dreptunghic cu lungimea unei catete egale cu 5cm si raza cercului inscris egala cu 2cm.

9. Rezolvati ecuatia

10. Pentru ce valori ale parametrului real m functia f : R® R, f(x) = 2(m²x + 3) - x(21 - mx) admite un minim de abcisa x = 0,5.

11. Rezolvati sistemul de ecuatii in multimea numerelor reale

12. Aria sectiunii diagonale a unei piramide patrulaterale regulate este egala cu aria bazei. Determinati volumul piramidei, daca lungimea muchiei laterale a piramidei este egala cu 5cm.

Solutii

1. Cum 49 < 143 < 343, rezulta (functia logaritmica f(x) = log_ax pentru a Î (0;1) este strict descrescatoare) sau

adica numarul

se afla intre numerele intregi -3 si -2.

2. De exemplu, f : R \ {3} ® R, . In adevar,

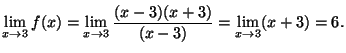
3. Se aplica formula termenii de rangul (k + 1) in dezvoltarea binomului (a + b)ⁿ

unde n = 6, k + 1 = 4, de unde k = 3,

. Rezulta

4. Se rezolva sistemul de ecuatii

si se obtin punctele de intersectie ale cercurilor date: A(0;0) si B(-2;2). Se scrie ecuatia dreptei ce trece prin aceste puncte:

de unde y = -x. Asadar ecuatia dreptei ce contine coarda data este y = -x.

5. Cum P(3 - i) = (3 - i)³ - 2(3 - i) - 7(3 - i) - 3 = 27 - 27i + 9i² - i³ - 18 + 12i - 2i² - 21 +
+ 7i - 3 = -22 - 7i, rezulta ca restul impartirii polinomului data la x - a, unde a = 3 - i este egal cu -22 - 7i.

7. Se aplica formula pentru determinarea volumului corpului de rotatie generat de rotatia in jurul axei Ox a subgraficului functiei f : [a,b] ® R

si se obtine

Fie ABC - triunghi dreptunghic (AC^BC) cu AC = 5cm si OD = OE = OF = r = 2cm. (O - centrul cercului inscris in triunghiul ABC). Fie BF = x. Atunci BD = x si cum CE = 2cm, (OECD - patrat) rezulta AE = AF = 3cm si AB = 3 + x. Se aplica teorema lui Pitagora

5² + (2 + x)² = (3 + x)²,

si se obtine x = 10cm. Prin urmare ipotenuza AB = 3 + 10 = 13(cm), iar raza cercului circumscris acestui triunghi

(cm) (centrul cercului circumscris triunghiului dreptunghic se afla in mijlocul ipotenuzei).

9. Domeniul valorilor admisibile (DVA) se determina din sistemul de inecuatii

de unde x Î (¥;-3) È (-3;3) È (5;+¥).

In DVA ecuatia este echivalenta cu

de unde se obtine ecuatia

Se tine seama de DVA si se considera doua cazuri:

x Î (¥;-3). Atunci |x + 3| = -(x + 3) si ecuatia devine 5(x - 3) = -(x - 5)(x + 3). Se rezolva ecuatia patrata obisnuita x² + 3x - 30 = 0 si se obtine si (nu verifica conditia x < -3).
x Î (-3;3) È (5;+¥). Atunci |x + 3| = x + 3 si ecuatia devine
5(x - 3) = (x - 5)(x + 3)
sau x² - 7x = 0, de unde x₁ = 0 si x₂ = 7.

Asadar, multimea solutiilor ecuatiei date este .

10. Functia data, f(x) = mx² + (2m² - 21)x + 6 pentru m ¹ 0, reprezinta un trinom patrat, ce admite minim in , daca

(parabola este cu ramurile in sus si varful ei se afla in

). Se rezolva sistemul si se obtine m = 3.

Pentru m = 0 functia f devine liniara si nu poate admite minim. Asadar m = 3.

11. Se aduna primele doua ecuatii si se obtine . Se multiplica prima ecuatie cu 2 si se aduna cu a treia ecuatie: . Din sistemul obtinut rezulta sau y = 16. In plus, sinx = 1 sau . Se substituie x si y in prima ecuatie (de exemplu) si se obtine z² = 9, de unde z = ±3. Asadar:

12.

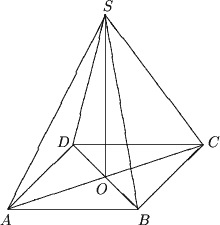
Fie SABCD - piramida patrulatera regulata cu SB = SC = SD = SA = 5cm, AB = a (latura patratului din baza), SO^AC (h = SO - inaltimea piramidei). Atunci , . S_ABCD = a². Conform ipotezei , de unde . Se considera triunghiul dreptunghic SOC si se obtine

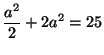, de unde a² = 10 si

(cm).

Asadar,