a 46-Olimpiada de Matematica a Republicii Moldova
Chisinau, 10-13 martie 2002
Prima zi, 11 martie 2002
Clasa a VII-a
7.1 La plecarea in vacanta 7 elevi au decis ca fiecare dintre ei va trimite exact la 3 colegi cate o carte postala fiecaruia. E posibil oare ca fiecare elev sa primeasca carti postale anume de la acei colegi carora el le-a scris? Argumentati raspunsul.
7.2 Numerele reale a, b si c satisfac relatia a + b + c = 1. Sa se demonstreze ca este adevarata inegalitatea a2 + b2 + c2 ≥ 4 (ab + ac + bc) – 1.
7.3 Fie unghiul ascutit Ð DEF, punctele fixe B si C pe
semidreapta (EF si punctul variabil A pe semidreapta (ED. Sa se determine pozitia punctului A pe
semidreapta (ED astfel incat suma
7.4 La un campionat de fotbal fara retur au participat 12 echipe. Conform regulamentului, pentru victorie
echipa obtine 2 puncte, pentru infrangere echipa nu obtine nici un punct, iar in caz de egalitate fiecare echipa obtine cate
un punct. Se stie ca la finele campionatului echipele au acumulat punctaje diferite, iar echipa clasata pe locul 2 a
acumulat un punctaj egal cu suma punctajelor acumulate de echipele clasate pe ultimele cinci locuri. A cui a fost victoria
in meciul dintre echipa clasata pe locul 4 si echipa clasata pe locul 8? Argumentati raspunsul.
Clasa a VIII-a
8.1 Sa se determine multimea tuturor solutiilor reale ale ecuatiei
| [x] + | é ç ë |
x + |
|
ù ÷ û |
+ | é ç ë |
x + |
|
ù ÷ û |
= 2002, |
8.2 Numarul natural nenul n poseda urmatoarea proprietate: pentru un careva numar natural nenul k exista k cifre care, fiind alipite la dreapta numarului n, formeaza impreuna cu acesta un numar egal cu suma primelor n numere naturale nenule. Sa se afle restul impartirii numarului n la 9.
8.3 Punctul P este interior cercului C(O,R). Pentru orice coarda [AB] a
cercului, care trece prin punctul P, sunt duse tangentele t1 si t2 la cerc
respectiv in punctele A si B. Punctele M si N sunt picioarele perpendicularelor duse din P
respectiv la t1 si t2. Sa se demonstreze ca marimea
8.4 Intr-o firma se instaleaza o statie interna de telefoane, fiecare numar telefonic fiind alcatuit din 4
cifre. Directorul firmei cere ca in birourile administrative ale firmei numerele de telefon sa contina doar cifrele 1, 2, 3
si oricare doua numere din acestea sa aiba cel mult o pozitie in care cifrele ar coincide. Care este numarul maxim de
telefoane ce pot fi instalate in birourile administrative ale acestei firme, respectand cerintele directorului?
Clasa a IX-a
9.1 Fie functia f : R ® R, f (x) = ax2 + bx + c, a ¹ 0 astfel ca (") xÎ[0,1] | f (x) | ≤ 1. Sa se determine cea mai mare valoare posibila a expresiei | a | + | b | + | c |.
9.2 Exista oare o putere cu exponent natural nenul a numarului 2 astfel incat prin permutarea cifrelor ei in scrierea zecimala sa se obtina un numar care ar fi o putere cu exponent natural a numarului 3? Argumentati raspunsul.
9.3 Sa se demonstreze ca pentru orice numar natural n ≥ 1 numarul
![]() nu este intreg.
nu este intreg.
9.4 Fie ABCD un patrulater convex, NÎ(AD) si
MÎ(BC) astfel incat ![]() Daca
Daca
Clasa a X-a
10.1 Trei aliage de metale pretioase contin aur in proportii diferite si au masele egale cu 1 kg, 2 kg si 3 kg. Este necesar de taiat fiecare aliaj in doua parti astfel incat din partile obtinute sa se obtina prin topire doua lingouri de mase 1 kg si 5 kg care contin aur in proportii identice. Explicati cum trebuie de procedat?
10.2 In plan sunt date n (n ≥ 3) puncte distincte necoliniare. Sa se arate cum poate fi construita o linie poligonala inchisa care trece prin fiecare punct.
10.3 Laturile [AB], [BC] si [AC] ale triunghiului ABC sunt tangente la cercul inscris de centru I in punctele C1, A1 si, respectiv, B1. Daca punctul B2 este mijlocul laturii [AC], sa se demonstreze ca dreptele B1I, A1C1 si BB2 sunt concurente.
10.4 In fiecare linie si fiecare coloana ale unui tabel de dimensiuni (2n+1) ´ (2n+1)
sunt scrise in mod arbitrar numerele 1, 2, ..., 2n, 2n+1. S-a constatat ca repartizarea numerelor in tabel
este simetrica in raport cu diagonala principala. Sa se demonstreze ca toate numerele de pe diagonala principala sunt distincte.
Clasa a XI-a
11.1 Sirul (an)n Î N*
este definit recurent a1Î(0,1),
an+1 = an (1 – an). Sa
se demonstreze ca ![]()
11.2 Pentru orice numar natural n si orice numar real x sa se demonstreze ca este adevarata
inegalitatea ![]()
11.3 Fie P un poliedru cu toate muchiile congruente si tangente la o sfera. Se stie ca una din fetele poliedrului P are un numar impar de laturi. Sa se demonstreze ca exista o sfera circumscrisa poliedrului P.
11.4 Printre numerele reale nenegative
a1, a2, ..., an exista cel putin doua nenule. Sa se compare
numerele
![]() si
si
![]()
Clasa a XII-a
12.1 Fie n Î N* si functia
f : [1, + ¥) ® R,
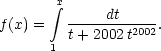 Sa se demonstreze ca pentru orice numere reale xi ≥ 1, i = 1, 2, ..., n,
este adevarata inegalitatea
Sa se demonstreze ca pentru orice numere reale xi ≥ 1, i = 1, 2, ..., n,
este adevarata inegalitatea
|
≤ ln |
|
. |
|
+ |
|
+ |
|
= 0 . |
12.3 Sa se rezolve in C ecuatia x5 – 20 x3 + 80 x – 80 = 0.
12.4 Pe tabla se scriu consecutiv numerele naturale dupa urmatoarea regula: primul numar scris pa tabla este
egal cu 4, iar fiecare numar ulterior scris pe tabla, insepand cu al doilea, se obtine prin inmultirea numarului scris precedent cu
3 si adunarea la produsul obtinut a numarului 4. Cate numere divizibile cu 2002 vor fi printre primele 2002 numere consecutive
scrise pe tabla?