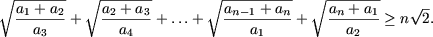Inegalitati

Inegalitati

In acest compartiment vor fi prezentate diverse metode de demonstrare a inegalitatilor, utilizand metodele propuse vor fi demonstrate atat inegalitati clasice precum si inegalitati propuse la diferite concursuri de matematica.

I. Monotonia functiilor

Se presupune ca cititorul este familiarizat cu notiunea de monotonie a functiilor si proprietatile (criteriile) functiilor monotone.

Problema 1. Sa se compare numerele e^p si p^e.

Solutie. Se considera functia

Deoarece derivata functiei f,

obtine valori negative pentru orice x Î (e;+Ľ) si f este continua pe [e;+Ľ) rezulta ca functia f este strict descrescatoare pe [e;+Ľ). Prin urmare, cum e < p se obtine

si deci e^p > p^e.

Problema 2. Sa se studieze marginirea sirului numeric

Solutie. Initial vom demonstra inegalitatea

ln(1 + x) Ł x (x ł 0). (1)

In acest scop, consideram functia

f:[0;+Ľ)Ž R; f(x) = x - ln(1 + x). Functia f este continue pe domeniul de definitie, si pentru orice x Î (0;+Ľ) are loc egalitatea

de unde conchidem ca f ˘(x) > 0 (x Î (0;+Ľ)). Prin urmare functia f este o functie strict crescatoare pe domeniul de definitie D(f), si deci f(x) ł f(0) ("x ł 0), de unde si rezulta inegalitatea (1).

In inegalitatea (1) se considera x = ¹/_n (n = 1,2,...) si se obtine

(2)

Din inegalitatile (2) deducem

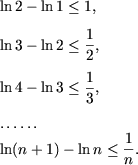(3)

Se sumeaza parte cu parte a inegalitatile (3) si se obtine inegalitatea

Cum

din ultima inegalitate rezulta ca sirul numeric x_n = 1 + ¹/₂ + ... + ¹/_n este nemarginit.

Consecinta: Seria este o serie divergenta.

Problema 3. (inegalitatea J.Bernoulli) Pentru orice x > -1; a > 1 are loc inegalitatea

(1 + x)^a ł 1 + ax. (4)

In plus, egalitatea are loc numai pentru x = 0.

Solutie. Consideram functia

f(x) = (1 + x)^a - 1 - ax, (x Î [-1;+Ľ)), unde a > 1 si a fixat in continuare.

Calculam derivata acestei functii:

f ˘(x) = a(1 + x)^a-1 - a = a((1 + x)^a-1 - 1) (x > -1). Deoarece a > 1, rezulta ca f ˘(x) < 0 pentru x Î (-1;0) si f ˘(x) > 0 pentru x Î (0;+Ľ) si prin urmare functia f este descrescatoare pe [-1;0] si crescatoare pe [0;+Ľ).

De aici, conchidem ca pentru orice x Î [-1;+Ľ)\{0} are loc inegalitatea f(x) > f(0), adica

(1 + x)^a - 1 - ax > 1 - 1 sau (1 + x)^a > 1 + ax (x Î [-1;0)Č(0;+Ľ), a > 1). Ramane de observat ca pentru x = 0 se obtine (1 + x)^a = 1 + ax.

Nota. Similar se demonstreaza si inegalitatile

(1 + x)^a Ł 1 + ax	(x ł -1; 0 < a < 1),
(1 + x)^a ł 1 + ax	(x ł -1; a < 0).

Problema 4. (inegalitatea W.Young) Daca p, q Î R\{0,1} poseda proprietatea ¹/_p + ¹/_q = 1; a, b sunt numere pozitive, atunci sunt adevarate inegalitatile

(5)

si

(6)

Mai mult, egalitate se atinge daca si numai daca a^p = b^q.

Solutie. Consideram cazul p > 1. Fixam un numar pozitiv a (a > 0) si examinam functia

Derivata acestei functii este f ˘(b) = b^q-1 - a, si prin calcule elementare se determina ca punctul

este un punct de minim local. Astfel

(7)

Din inegalitatea (7) tinand seama ca ¹/_p + ¹/_q = 1 se obtine

si deci inegalitatea (5) este demonstrata. Mai mult, din (7) rezulta ca egalitatea are loc numai in cazul in care

adica daca a^p = b^q.

Inegalitatea (6) se demonstreaza in mod similar.

Problema 5. Sa se demonstreze inegalitatea

|sinx| Ł |x| (x Î R). (8)

In acest scop, consideram functia

f:[0;1]Ž R, f(x) = x - sinx. Derivata functiei f are forma f ˘(x) = 1 - cosx (x Î [0;1]). In baza marginirii functiei cosinus (|cosx| Ł 1; x Î R), deducem ca f ˘(x) ł 0, care la randul sau implica ca functia f este monoton crescatoare pe domeniul sau de definitie, si deci are loc inegalitatea f(x) ł f(0) (x Î [0;1]), sau x - sinx ł 0, (x Î [0;1]) de unde rezulta inegalitatea initiala.

Problema 6. Sa se arate ca

a²(b - c) + b²(c - a) + c²(a - b) > 0, daca a > b > c.

Solutie. Examinam functia f:[0;+Ľ)ŽR de forma

f(t) = (b + t)²(b - c) + b²(c - (b + t)) + c²((b + t) - b), unde a, b, c sunt parametri reali ce verifica inegalitatea a > b > c. Similar problemelor precedente, se demonstreaza ca functia f este strict crescatoare pe [0;+Ľ), si deci are loc inegalitatea f(a - b) > f(0). Ultima inegalitate este echivalenta cu inegalitatea din enunt.

II. Convexitatea

Definitie: Functia f : IŽR (I un interval al axei reale) se numeste convexa pe I daca pentru orice x₁, x₂ Î I si orice l₁ l₂ cu proprietatea l₁ ł 0, l₂ ł 0, si l₁ + l₂ = 1, are loc inegalitatea

f(l₁x₁ + l₂x₂) Ł l₁f(x₁) + l₂f(x₂). (9)

In cazul in care pentru orice x₁ š x₂, l₁·l₂ š 0 semnul inegalitatii (9) este strict vom spune ca functia f este strict convexa pe I.

Similar se defineste si notiunea de functie concava (strict concava), schimband semnul inegalitatii in (9).

Inegalitatea J. Jensen. Fie functia f : IŽR convexa pe I. Atunci pentru orice x_j Î I (j = 1,...,n) si orice l_j ł 0 (j = 1,...,n); l₁ + ... + l_n = 1 are loc inegalitatea

Criteriu de convexitate

Fie f : IŽR, f continue pe I si poseda derivata de ordinul doi pe int(I), unde int(I) este interiorul intervalului I, adica int(I) = {x Î R | $e > 0 (x - e, x + e Ě I)}. Functia f este convexa pe I daca si numai daca f ˘˘(x) ł 0 (x Î int(I)). Mai mult daca f ˘˘(x) > 0 (x Î int(I)) atunci functia f este strict convexa pe I.

Nota. Afirmatiile similare cu inegalitatea Jensen si criteriul anterior sunt adevarate si pentru functiile concave (convexe in jos).

Problema 7. (Inegalitatea Cauchy despre medii). Pentru orice numere nenegative x₁, x₂, ..., x_n este adevarata inegalitatea

(10)

Altfel, media geometrica nu intrece media aritmetica.

Solutie. Daca unul dintre numerele a_j este 0 (a_j = 0 pentru un j Î {1,...,n}), atunci inegalitatea (10) este evidenta.

Fie a_j > 0 (j = 1,...,n). Consideram functia f(x) = lnx (x > 0). Cum rezulta ca functia f este concava pe multimea (0;+Ľ). In baza inegalitatii Jensen deducem

care implica inegalitatea (10).

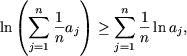
Problema 8. Fie x₁, ..., x_n numere nenegative. Sa se arate ca functia

este monoton crescatoare.

Solutie. Fie 0 < a < b. Consideram functia (x ł 0). Deoarece (x > 0), rezulta ca h este convexa pe [0;+Ľ). Conform inegalitatii Jensen conchidem

de unde rezulta f(a) Ł f(b).

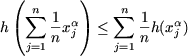
Problema 9. Sa se arate ca

, unde a, b, g sunt unghiurile interioare a unui triunghi.

Solutie. Consideram functia f : [0;p]ŽR; f(x) = sinx. Cum f ˘˘(x) = -sinx si f ˘˘(x) < 0 pentru x Î (0;p), rezulta ca f este o functie concava pe [0;p]. In baza inegalitatii Jensen se obtine

adica

Problema 10. Sa se arate ca pentru orice numere pozitive a_j, b_j (j = 1,...,n) are loc inegalitatea

Solutie. Consideram functia f : [0;+Ľ)ŽR, f(x) = lnx. Aceasta functie este concava (a se vedea Problema 7) si in baza inegalitatii Jensen

si deci

Problema 11. (Inegalitatea Göughens) Sa se demonstreze ca este adevarata inegalitatea

unde a_j ł 0 (j = 1,...,n).

Solutie. Fie f : RŽR, f(x) = ln(1 + e^x). Sa cercetam convexitatea acestei functii. In acest scop, calculam a doua derivata a functiei f: (x Î R). Cum f ˘˘(x) > 0 pentru orice x Î R, aplicand inegalitatea Jensen, obtinem

III. Ordonarea

Afirmatia 1. Fie date doua cortegii de cate n numere, astfel incat

a₁ ł a₂ ł ... ł a_n,

b₁ ł b₂ ł ... ł b_n.

Desemnam prin s o suma de forma

s = a₁b_i₁ + ... + a_nb_{i_n}, unde (i₁,...,i_n) este o permutare a numerelor 1,2,...,n. Atunci

S = max s = a₁b₁ + ... + a_nb_n,

s = min s = a₁b_n + ... + a_nb₁.

Problema 12. Sa se arate ca

daca a, b, c sunt numere pozitive.

Solutie. Deoarece inegalitatea este simetrica, fara restrictia generalitatii vom presupune ca a ł b ł c. Atunci

Prin urmare

Sumand parte cu parte ultimele doua inegalitati se obtine

Problema 13. Sa se arate ca pentru orice numere pozitive a, b, c, cu proprietatea a·b·c = 1 are loc inegalitatea

Solutie. Similar Problemei 12 vom presupune a ł b ł c. Atunci,

Prin urmare

si cum ab ł ac ł bc, in baza Afirmatiei 1 se obtine

Sumand parte cu parte ultimele doua inegalitati deducem

(11)

Conform inegalitatii Cauchy despre medii (a se vedea Problema 7) avem

(12)

Astfel, din (11) si (12) tinand seama ca a·b·c = 1, rezulta inegalitatea

Problema 14. Fie a, b, c numere pozitive. Sa se demonstreze ca

(a^ab^bc^c)² ł a^b+cb^c+ac^a+b.

Solutie. Fara restrictia generalitatii presupunem ca a ł b ł c. Atunci lna ł lnb ł lnc. Prin urmare, conform Afirmatiei 1,

alna + blnb + clnc ł blna + clnb + alnc si alna + blnb + clnc ł clna + alnb + blnc. Sumam parte cu parte, inegalitatile si obtinem 2(alna + blnb + clnc) ł (b + c)lna + (c + a)lna + (c + a)lnb + (a + b)lnc sau, echivalent, ln(a^ab^bc^c)² ł ln(a^b+cb^c+ac^a+b), de unde rezulta (a^ab^bc^c)² ł a^b+cb^c+ac^a+b.

Problema 15. Sa se arate ca pentru orice numere pozitive a, b, c este adevarata inegalitatea

a³b + b³c + c³a ł a²bc + b²ca + c²ab.

Solutie. Fie a ł b ł c. Atunci

a² ł b² ł c² si

in baza Afirmatiei 1 conchidem,

Ultima inegalitate este echivalenta cu cea din enunt.

Problema 16. Fie {a₁, a₂, ..., a_n} Ě N. Sa se arate ca pentru orice n Î N are loc inegalitatea

Solutie. Fie a_i₁ < a_i₂ < ... < a_{i_n}, unde (i₁,i₂,...,i_n) este o permutare a numerelor 1,2,...,n. Cum

rezulta

IV. Inegalitati clasice si aplicatii

Problema 17. (Inegalitatea Hölder) Sa se arate ca pentru orice numere pozitive p, q cu proprietatea ¹/_p + ¹/_q = 1 si orice numere reale a_j, b_j (j = 1,...,n) are loc inegalitatea

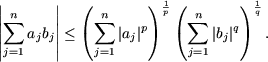
(13)

Solutie. Presupunem ca si (in caz contrar inegalitatea (13) este evidenta). Din inegalitatea Young (a se vedea Problema 5), se obtine

de unde nemijlocit rezulta inegalitatea (13).

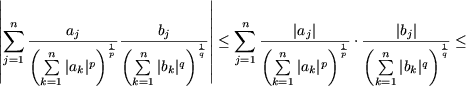
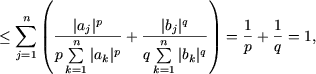
Problema 18. Sa se arate ca sirul

este crescator.

Solutie. Conform inegalitatii Cauchy despre medii (a se vedea Problema 7) au loc inegalitatile

de unde rezulta

adica x_n Ł x_n+1.

Problema 19. Sa se demonstreze ca

(14)

pentru orice x_k Î R; x_k > 0 (k = 1,...,n).

Solutie. Inegalitatea (14) rezulta imediat din inegalitatea Cauchy:

Problema 20. Sa se arate ca pentru orice numere pozitive a₁, a₂, ..., a_n are loc inegalitatea

Solutie. Conform inegalitatii Cauchy-Buneacovski (cazul particular al inegalitatii Hölder, p = q = 2) obtinem

Problema 21. Sa se arate ca

unde a_k ł 0 (k = 1,2,...,n).

Solutie. Conform inegalitatii Cauchy-Buneacovski (inegalitatea Hölder in cazul p = q = 2) deducem

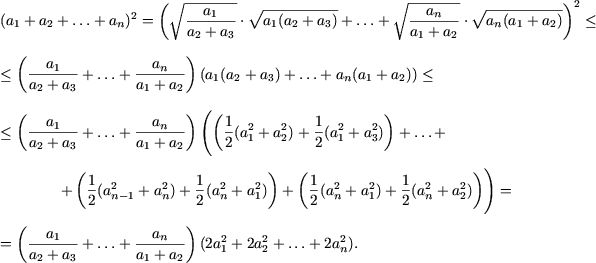
Problema 22. Sa se arate ca pentru orice numere pozitive a_j, b_j (j = 1,...,n) are loc inegalitatea

Solutie. In baza inegalitatii Göughens obtinem

de unde rezulta ca

Exercitii pentru autoevaluare

Sa se demonstreze inegalitatea
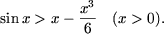
Sa se compare numerele
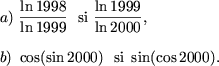
Sa se arate ca pentru x > 0 are loc inegalitatea 1 + 2lnx Ł x².
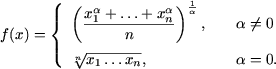
Fie x₁, x₂, ..., x_n numere pozitive. Sa se demonstreze ca functia f : RŽR, este monoton crescatoare. Mai mult, functia f este strict crescatoare daca si numai daca x₁ = x₂ = ... = x_n.
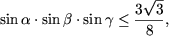
Sa se demonstreze inegalitatea unde a, b, g sunt unghiurile interioare ale unui triunghi.
Fie a₁, a₂, ..., a_n numere reale cu proprietatile a_k Î (0;¹/₂) (k = 1,...,n) si a₁ + ... + a_n = 1. Sa se arate ca
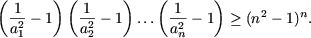
Sa se demonstreze inegalitatile unde a, b, c sunt numere pozitive.
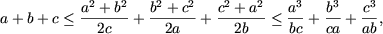
(Inegalitatea Cebasev) Daca a₁ ł a₂ ł ... ł a_n; b₁ ł b₂ ł ... ł b_n, atunci (a₁ + a₂ + ... + a_n)(b₁ + b₂ + ... + b_n) Ł n(a₁b₁ + a₂b₂ + ... + a_nb_n).
Daca 1 < a Ł b Ł c, atunci
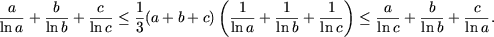
Sa se arate ca
Sa se arate ca pentru orice numere nenegative a, b, c are loc inegalitatea (a + b)(b + c)(c + a) ł 8abc.
Sa se arate ca pentru orice numere reale x₁, ..., x_n are loc inegalitatea
Sa se demonstreze ca sirul este monoton descrescator.
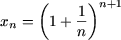
Sa se arate ca
Sa se demonstreze ca pentru orice numere pozitive a₁, a₂, ..., a_n are loc inegalitatea