Principiul inductiei matematice constituie un mijloc important de demonstratie in matematica a propozitiilor (afirmatiilor) ce depind de argument natural.
Metoda inductiei matematice consta in urmatoarele:
O propozitie (afirmatie) oarecare P(n), ce depinde de un numar natural n, este adevarata pentru orice n natural, daca:
- P(1) este o propozitie (afirmatie) adevarata;
- P(n) ramane o propozitie (afirmatie) adevarata, cand n se majoreaza cu o unitate, adica P(n + 1) este adevarata.
Asadar, metoda inductiei presupune doua etape:
- Etapa de verificare: se verifica daca propozitia P(1) este adevarata;
- Etapa de demonstrare: se presupune ca propozitia P(n) este adevarata si se demonstreaza justetea afirmatiei P(n + 1) (n a fost majorat cu o unutate).
Nota 1. In unele cazuri metoda inductiei matematice se utilizeaza in urmatoarea forma:
Fie m un numar natural, m > 1 si P(n) o propozitie ce depinde de n, n ³ m.
Daca
- P(m) este adevarata;
- P(n) fiind o propozitie justa implica P(n + 1) adevarata pentru n ³ m, atunci P(n) este o propozitie adevarata pentru orice numar natural n ³ m.
In continuare sa ilustram metoda inductiei matematice prin exemple.
Exemplul 1. Sa se demonstreze urmatoarele egalitati
Rezolvare. a) Pentru n = 1 egalitatea devine
1=1,
prin urmare P(1) este adevarata.
Presupunem ca egalitatea din enunt este adevarata, adica are loc
egalitatea
,
Asadar, conform principiului inductiei matematice egalitatea din enunt este justa pentru orice n natural.
Nota 2. Mentionam ca acest exemplu poate fi rezolvat si fara
utilizarea inductiei matematice. Intr-adevar, suma 1 + 2 + 3 + ... + n
reprezinta suma primilor n termeni ai progresiei aritmetice cu primul
termen a1 = 1 si ratia d = 1. In baza formulei cunoscute
se obtine
b) Pentru n = 1 egalitatea devine 2·1 - 1 = 12 sau 1=1, astfel P(1) este justa. Presupunem justa egalitatea
Se tine seama de egalitatea din enunt si se obtine
Asadar P(n + 1) este adevarata si, prin urmare, egalitatea din enunt este adevarata.
Nota 3. Similar exemplului precedent, se rezolva si fara a aplica metoda inductiei matematice.
c) Pentru n = 1 egalitatea este justa
1=1. Se presupune justa egalitatea
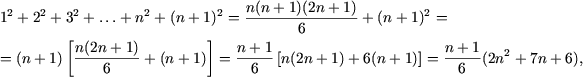
si cum 2n2 + 7n + 6 = (2n + 3)(n + 2) se obtine
d) Pentru n = 1 egalitatea este justa:
1=1.
Se presupune ca are loc egalitatea
In adevar, tinand seama de ipoteza
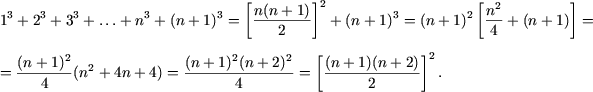
e) Propozitia P(1) este justa
2=2. Se presupune ca egalitatea
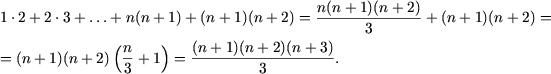
Asadar, egalitatea enuntata este justa pentru orice n natural.
f) P(1) este adevarata:
1/3 = 1/3. Se presupune
ca are loc P(n):
In adevar, tinand seama de justetea afirmatiei P(n), se obtine
Prin urmare, egalitatea este demonstrata.
g) Pentru n = 1 egalitatea devine a + b = b + a, si deci este adevarata.
Fie formula binomului Newton este justa pentru n = k, adica
se obtine
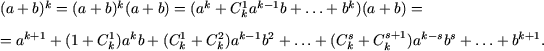
Exemplul 2. Sa se demonstreze inegalitatile
| a) inegalitatea Bernuolli: (1 + a)n ³ 1 + na, a > -1, n Î N. |
b) x1 + x2 + ...
+ xn ³ n,
daca
x1x2·
... ·xn = 1
si xi > 0,
 .
|
c) inegalitatea Cauchy relativa la media aritmetica si geometrica
unde xi > 0,
,
n ³ 2.
|
| d) sin2na + cos2na £ 1, n Î N. |
e) 
|
| f) 2n > n3, n Î N, n ³ 10. |
Rezolvare. a) Pentru n = 1 inegalitatea este adevarata
|
|
(1) |
In adevar, cum a > -1 implica a + 1 > 0, multiplicand ambii membri ai inegalitatii (1) cu (a + 1) se obtine
Asadar P(n) adevarata implica P(n + 1) adevarata, prin urmare, conform principiului inductiei matematice inegalitatea Bernoulli este adevarata.
b) Pentru n = 1, se obtine x1 = 1, si, prin urmare x1 ³ 1, adica P(1) este o afirmatie justa. Se presupune ca P(n) este adevarata, adica, x1,x2,...,xn sunt n numere pozitive, prodususul carora este egal cu unu, x1x2·...·xn = 1, si x1 + x2 + ... + xn ³ n.
Sa aratam, ca aceasta ipoteza implica justetea urmatoarei afirmatii: daca x1,x2,...,xn,xn+1 sunt (n + 1) numere pozitive cu x1x2·...·xn·xn+1 = 1 atunci x1 + x2 + ... + xn + xn + 1 ³ n + 1.
Se disting urmatoarele doua cazuri:
1) x1 = x2 = ... = xn = xn+1 = 1 si atunci suma lor este (n + 1), inegalitatea fiind justa,
2) cel putin un numar este diferit de unu, fie mai mare ca unu. Atunci, dat fiind x1x2· ... ·xn·xn + 1 = 1, rezulta ca exista cel putin inca un numar diferit de unu, mai exact, mai mic ca unu. Fie xn + 1 > 1 si xn < 1. Consideram n numere pozitive
Cum
= n + 1 + xn+1(1 - xn) - (1 - xn) = n + 1 + (1 - xn)(xn+1 - 1) ³ n + 1
Nota 4. Se observa, ca semnul egalitatii are loc daca si numai daca x1 = x2 = ... = xn = 1.
c) Fie x1,x2,...,xn numere pozitive arbitrare. Se considera n numere
Nota 5. Semnul egalitatii are loc daca si numai daca
x1 = x2 = ... = xn.
d) P(1) este o afirmatie justa: sin2a + cos2a = 1. Se presupune ca P(n) este o afirmatie adevarata:
e) Pentru n = 1 afirmatia este justa:
1 < 3/2.
Se presupune ca
si urmeaza de a demonstra ca
f) Se tine seama de nota 1 si se verifica P(10): 210 > 103, 1024 > 1000, asadar pentru n = 10 inegalitatea este justa. Se presupune ca 2n > n3 (n > 10) si trebuie de demonstrat P(n + 1), adica 2n+1 > (n + 1)3.
Cum pentru n > 10 avem
sau
rezulta
Asadar conform principiului inductiei pentru orice n Î N, n ³ 10 avem 2n > n3.
Exemplul 3. Sa se demonstreze ca pentru orice n Î N
| a) n(2n2 - 3n + 1) se divide cu 6, |
| b) 62n-2 + 3n+1 + 3n-1 se divide cu 11. |
Rezolvare. a) P(1) este o propozitie adevarata ( 0 se divide cu 6). Fie P(n) are loc, adica n(2n2 - 3n + 1) = n(n - 1)(2n - 1) se divide cu 6. Se arata, ca are loc P(n + 1) adica (n + 1)n(2n + 1) se divide cu 6. In adevar, cum
| n(n + 1)(2n + 1) = n(n - 1 + 2)(2n - 1 + 2) = (n(n - 1) + 2n)(2n - 1 + 2) = |
| = n(n - 1)(2n - 1) + 2n(n - 1) + 2n(2n + 1) = n(n - 1)(2n - 1) + 2n·3n = |
| = n(n - 1)(2n - 1) + 6n2 |
Asadar P(n + 1) este o afirmatie justa, si n(2n2 - 3n + 1) se divide cu 6 pentru orice n Î N.
b) Se verifica P(1): 60 + 32 + 30 = 11, prin urmare P(1) este justa. Urmeaza sa se arate, ca daca 62n-2 + 3n+1 + 3n-1 se divide cu 11 (P(n)), atunci 62n + 3n+2 + 3n de asemenea se divide cu 11 (P(n + 1)). In adevar, cum
Exemplul 1. Sa se calculeze latura
a unui poligon regulat
cu 2n laturi inscris intr-o circumferinta de raza R.
Rezolvare. Pentru n = 2 poligonul regulat cu 22 laturi reprezinta
un patrat, si in acest caz a4 =
R
.
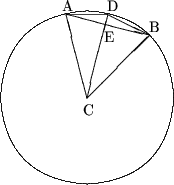
Fie 
si sa determinam
.
Daca AB = a¢, atunci
AE = a¢/2;
BD = a¢¢.
Din triunghiul DEB, conform teoremei Pitagora
si deci,
|
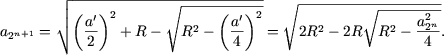
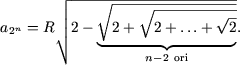
(2) |
Cum a fost arata anterior, pentru n = 1 aceasta formula este adevarata.
Fie (2) adevarata pentru n = k.
Sa calculam
. Conform
formulei de trecere se obtine
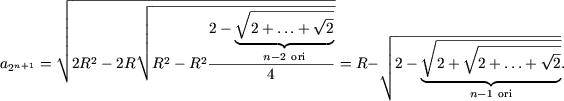
Nota. Din (2) rezulta ca lungimea circumferintei este egala cu
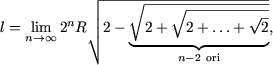
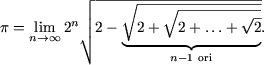
I. Sa se demonstreze egalitatile:
|
|
|
|
|
|
|
|
|
|
|
|
|
II. Sa se demonstreze inegalitatile
III. Sa se demonstreze, ca pentru orice numar natural, numarul an se divide cu b
| a) an = 5n+3 + 113n+1, b = 17, |
| b) an = 11n+2 + 122n+1, b = 133, |
| c) an = 2n3 + 3n2 + 7n, b = 6, |
| d) an = 10n + 18n - 28, b = 27, |
| e) an = n5 - n, b = 30. |
IV. Sa se arate, ca
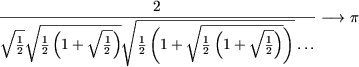(Formula lui Viete).
V. Sa se calculeze razele rn, Rn a circumferintelor inscrise si circumscrise poligonului regulat cu 2n laturi de perimetru p.
VI. Sa se determine in cate triughiuri poate fi divizat un poligon cu n laturi de diagonalele sale neconcurente.
VII. Fie date n patrate arbitrare. Sa se arate ca aceste patrate pot
fi taiate in asa mod incat din partile obtinute se poate de format
un patrat.