| Pagina principala | Ghidul utilizatorului | Rubrica candidatului | Curriculumurile scolare |
| Matematica competitiva | Matematica distractiva| Formule, dictionare | Avizuri |
|Pagini din istorie | Examene, teste | Bibliografie | Link-uri | Site map |


Numere Fibonacci

Problema iepurilor

Fie data o pereche de iepuri. Se stie ca fiecare pereche de iepuri produce in fiecare luna o noua pereche de iepuri, care la randul sau devine productiva la varsta de o luna. Sa se determine cate perechi de iepuri vor fi dupa n luni.

Initial vom remarca istoria acestei probleme si apoi solutia ei, precum si alte probleme ce tin de ea.

Vorbind de matematica din antichitate fiecare ar numi asa matematicieini ca Euclide, Pytagoras, Heron s.a. Unul dintre cei mai ilustri matematicieni a Evului Mediu, de rand cu Viete, ar fi Leonardo din Pisa, cunoscut sub numele Fibonacci (prescurtare de la filus Bonacci, adica fiul lui Bonacci).

Fibonacci, nascut in Italia, in 1175, a fost educat in Nordul Africii, unde tatal sau detine un post diplomatic. Revenind in Italia, in 1202 publica un tratat de matematica cu titlul "Liber abaci". Acest tratat contine aproape toata informatia acelui timp, referitoare la aritmetica si algebra, si care a avut un rol important pe parcursul urmatoarelor secole in dezvoltarea matematicii in Europa. In particular, in baza acestui tratat, europenii au luat cunostinta de scrierea arabica a numerelor, adica de sistemul de numeratie pozitional arab. La fel, in 1220 publica "Practica geometrica", in 1225 "Liber quadratorum". Tratatul "Liber abaci" a fost reeditat in 1228. Una din problemele discutate in "Liber abaci" este anume "problema iepurilor", (p. 123-124 in editia anului 1228) prezentata la inceputul acestui material.

Sa trecem la rezolvarea acestei probleme.

Fie fn numarul de perechi de iepuri dupa n luni. Numarul de perechi de iepuri dupa n + 1, notat prin fn+1, va fi numarul de perechi la luna n, adica fn, plus numarul de iepuri nou-nascuti. Cum iepuri se nasc din pereche de iepuri cu varsta mai mare de o luna, iepuri nou-nascuti vor fi fn-1 perechi.

Prin urmare se obtine relatia
fn+1 = fn + fn-1. (1)

In plus,
f0 = 0     si     f1 = 1. (2)

Asadar am obtinut un sir numeric definit in mod recurent. Scriind termenii acestui sir, determinam
0, 1, 1, 2, 3, 5, 8, ... (3)
numit sirul Fibonacci. Fiecare termen al sirului, incepand cu al treilea, este egal cu suma precedentilor doi termeni. Primii doi termeni se considera fiind dati, f0 = 0, f1 = 1.

Astfel "problema iepurilor" s-a redus la rezolvarea ecuatiei functionale (1), adica la determinarea termenului general fn a sirului, care verifica relatia (1) in conditiile (2).

Presupunem ca sirul fn are forma
fn = ln, (4)
unde l un parametru real.

Substituim fn in (1), si obtinem

ln+1 = ln + ln-1,
sau echivalent
ln-1(l2 - l - 1) = 0.
Cum fn ¹ 0     ("n Î N*), ultima egalitate devine
l2 - l - 1, (5)
care reprezinta o ecuatie patrata in raport cu parametrul real l. Din (5) deducem
Asadar, sirurile
verifica egalitatea (1). De aici, conchidem ca ecuatia (1) poseda mai multe solutii. In general exista o infinitate de siruri care verifica (1). Usor de observat ca sirul de forma
(6)
unde c1, c2 - constante reale fixate, la fel verifica (1). Mai mult, se poate arata ca orice sir ce verifica egalitatea (1) are forma (6). Avand alte scopuri, nu vom demonstra acest fapt in cadrul acestei lucrari. Pentru cei interesanti in teoria generala de solutionare a ecuatiilor de forma (1), numite ecuatii cu diferente finite, recomandam sa consulte [1]-[4].

Revenind la sirul Fibonacci, constatam ca acest sir se determina univoc, si unicitatea este dictata de primii doi termeni, adica de conditiile initiale (2). Sunstituind n = 0 si n = 1 in (6), se obtine sistemul liniar

cu solutia

In final, termenul de rang n al sirului Fibonacci are forma
(7)

Proprietati ale sirului Fibonacci.

1°. f1 + f2 + ... + fn = fn+2 - 1. (8)

Demonstratie.

f1 = f3 - f2
f2 = f4 - f3
...
fn-1 = fn+1 - fn
fn = fn+2 - fn+1.

Sumand parte cu parte egalitatile anterioare se obtine

f1 + f2 + ... + fn = fn+2 - f2,
si cum f2 = 1 se obtine egalitatea (8).

2°. f1 + f3 + f5 + ... + f2n-1 = f2n.

3°. f2 + f4 + ... + f2n = f2n+1 - 1.

Proprietatile 2° - 3° se demonstreaza similar cu 1°.

4°. f12 + f22 + ... + fn2 = fn·fn+1. (9)

Demonstratie. Se observa cu usurinta ca are loc relatia

fn·fn+1 - fn-1fn = fn(fn+1 - fn-1) = fn2     (n Î N).

Din aceasta relatie, deducem egalitatile

f12 = f1·f2,
f22 = f2·f3 - f1·f2,
f32 = f3·f4 - f2·f3,
...
fn2 = fn·fn+1 - fn-1·fn.
Sumand parte cu parte egalitatile precedente se obtine egalitatea (9).

5°. Sa se arate ca   fn+m = fn-1·fm + fn·fm+1, (10)
unde fn desemneaza termenul de rang n al sirului Fibonacci.

Demonstratie. Desigur, cunoscand forma generala a termenului fn (a se vedea (9) se poate de substituit in (10) si de aratat ca are loc egalitatea. Cu toate acestea, vom demonstra (10) utilizand metoda inductiei matematice. Vom face inductia dupa m Î N.

Pentru m = 1, egalitatea (10) devine

fn+1 = fn-1·f1 + fn·f2,
care este evidenta. Pentru m = 2 formula (10) la fel este evidenta. Intr-adevar,
fn+2 = fn-1f2 + fnf3 = fn-1 + 2fn = fn-1 + fn + fn = fn+1 + fn.

Astfel baza inductiei este verificata (m = 1; m = 2). Fie (10) este adevarata pentru m = k si m = k + 1 si vom demonstra ca este adevarata si pentru m = k + 2.

Asadar, fie sunt adevarate egalitatile

fn+k = fn-1fk + fnfk+1,
fn+k+1 = fn-1fk+1 + fnfk+2.
Sumand parte cu parte ultimele egalitati, se obtine
fn+k+2 = fn-1·fk+2 + fn·fk+3,
care si reprezinta egalitatea (10) pentru m = k + 2.

6°. f2n = fn-1fn + fn·fn+1.

Demonstratia rezulta din (10) punand m = n.

7°. Termenul f2n se divide prin fn.

Demonstratie. Din 6° rezulta

f2n = fn(fn-1 + fn+1),
de unde rezulta ca f2n fn.

8°.

9°.

Proprietatile 8° - 9° fiind consecinte directe din 6°, raman sa fie demonstrate independent.

10°. fn2 = fn-1fn+1 + (-1)n+1 (11)

Demonstratie. Vom demonstra egalitatea (11) prin inductie dupa n. Pentru n = 2 egalitatea (11) devine

f22 = f1·f3 - 1,
care este adevarata.

Fie (11) este adevarata pentru n si vom demonstra ca este adevarata si pentru n + 1. Asadar fie are loc egalitatea

fn2 = fn-1·fn+1 + (-1)n+1.
Adunam la ambele parti ale ultimei egalitati fn·fn+1. Ca rezultat se obtine
fn2 + fn·fn+1 = fn-1·fn+1 + fn·fn+1 + (-1)n+1,
sau echivalent
fn(fn + fn+1) = fn+1(fn-1 + fn) + (-1)n+1,
si cum fn+2 = fn + fn+1 (a se vedea definitia sirului Fibonacci) deducem
fnfn+2 = fn+12 + (-1)n+1,
sau
fn+12 = fn·fn+2 + (-1)n+2.
Deci (11) este adevarata si pentru n + 1.

11. Sa se arate ca daca n este divizibil prin m atunci fn este divizibil prin fm.

Demonstratie. Fie n m, adica n = mk. Vom demonstra proprietatea (11) prin inductie dupa k. Pentru k = 1, n = m, si deci, fn evident este divizibil prin fm. Presupunem ca fmk este divizibil prin fm. Sa examinam fm(k+1). Cum fm(k+1) = fmk+m si utilizand egalitatea (10) se obtine

fm(k+1)2 = fmk-1fm + fmk·fm+1.
Primul termen al sumei din dreapta evident este divizibil prin fm. Termenul al doilea este divizibil prin fm conform presupunerii inductive. Prin urmare suma acestor termeni este divizibila prin fm, si deci, fm(k+1) fm. Proprietatea 11° este demonstrata.

Alte proprietati ce tin de divizibilitate, geometrie, teoria algoritmilor etc. pot fi consultate in Bibliografia indicata la sfarsitul acestei lucrari.

Exercitii pentru lucrul individual

  1. Fie (fn)n Î N sirul Fibonacci. Sa se demonstreze ca

    1. f1f2 + f2f3 + f3f4 + ... + f2n-1·f2n = f2n2
    2. f1f2 + f2f3 + ... + f2nf2n+1 = f2n+12 - 1
    3. nf1 + (n - 1)f2 + ... + 2fn-1 + fn = fn+4 - (n + 3)
    4. f1 + 2f2 + 3f3 + ... + nfn = nfn+2 - fn+3 + 2

  2. Sa se arate ca pentru orice m Î N, printre primele m2 - 1 numere Fibonacci exista unul divizibil prin m.
  3. Sa se demonstreze ca:

    1. Numarul Fibonacci fn este par daca si numai daca n este divizibil prin 3;
    2. Numarul Fibonacci fn este divizibil prin 3 daca si numai daca rangul lui este divizibil prin 4;
    3. fn 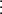4 daca si numai daca n 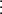6;
    4. fn 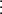5 daca si numai daca n 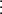5;
    5. fn 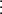7 daca si numai daca n 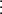8;
    6. fn 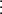16 daca si numai daca n 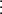12.

Bibliografie


| Pagina principala | Ghidul utilizatorului | Rubrica candidatului | Curriculumurile scolare |
| Matematica competitiva | Matematica distractiva| Formule, dictionare | Avizuri |
|Pagini din istorie | Examene, teste | Bibliografie | Link-uri | Site map |