Principiul extremal

Ideea-cheie a solutionarii unui sir de probleme consta in studierea unei marimi (element, caracteristica) extremale. Aceasta metoda de rezolvare se numeste pricipiul extremal. Sa analizam cateva exemple.

Exemplul 1. Sa se demonstreze ca multimea numerelor prime de forma 4m + 3, m Î N, este infinita.

Rezolvare. Admitem contrariul, adica presupunem ca multimea numerelor prime de forma 4m + 3 este finita. Fie p₁, ¼,p_n elementele acestei multimi. Daca n este numar par, atunci

p₁·p₂·¼·p_n + 2 ≡ (-1)ⁿ + 2 ≡ 3 (mod 4), adica p₁·p₂·¼·p_n + 2 = 4m + 3 pentru un oarecare m Î N. Prin urmare acest numar are un divizor prim de forma p = 4k + 3 (in adevar, daca toti divizorii primi ai numarului 4m + 3 au forma 4k + 1, atunci si produsul lor va avea forma 4k + 1). Pe de alta parte, este usor de observat ca nici unul din numerele p₁,p₂,¼,p_n nu sunt divizori ai numarului p₁·p₂·¼·p_n + 2. Prin urmare, p Ï {p₁,p₂,¼, p_n}. Contradictie cu ipoteza ca toate numerele prime de forma 4m+3 se contin in multimea {p₁,p₂,¼,p_n}.

Daca n este un numar impar, atunci

p₁·p₂·¼·p_n + 4 ≡ (-1)ⁿ + 4 ≡ 3 ( mod 4). Similar cazului precedent se arata existenta unui numar prim p de forma p = 4k + 3, astfel incat p Ï {p₁,p₂,¼,p_n}. Aceeasi contradictie.

Exemplul 2. Sa se demonstreze ca pentru orice n natural, numarul

(1)

nu este natural.

Rezolvare. Fie puterea maximala a lui trei, ce divide numarul 2j + 1 (j = 0,1,¼,n) si 3^r = max{ | j = 0,1,¼,n}. Vom arata ca numai pentru un j Î {0,1,¼,n} are loc egalitatea r = r_j. Admitem contrariul. Fie j,k Î {0,1,¼,n}, j ≠ k astel incat

2j + 1 = 3^r·s_j, 2k + 1 = 3^r·s_k. Din forma numarului 3^r, rezulta 3^r+1 > 2n+1. Prin urmare 1 ≤ 3^r·s_j < 3^r+1, 1 ≤ 3^r·s_k < 3^r+1, de unde rezulta, 1 ≤ s_j ≤ 2, 1 ≤ s_k ≤ 2. Cum s_j ≠ s_k, unul din aceste numere este par. Contradictie cu ipoteza.

Aducand expresia (1) la numitor comun se obtine

(2)

unde (2n + 1)!! = 1·3·¼·(2n + 1).

Fie r = r_j si 3^m - puterea maximala a numarului trei ce divide numarul (2n+1)!!. Atunci pentru fiecare k ≠ j din relatia rezulta ca . Pe de alta parte . Asadar

si, prin urmare, numarul (2) nu este natural.

Exemplul 3. Sa se demonstreze ca ecuatia

x² + y² = 3(z² + t²) (3)
nu are solutii in numere intregi pozitive.

Rezolvare. Presupunem contrariul, adica exista solutiile x, y, z, t a ecuatiei (3) in numere intregi pozitive. Din (3) rezulta ca 3|x² + y² si, prin urmare, 3|x si 3|y (rezulta din faptul ca restul impartirii patratului oricarui numar intreg la 3 este egal cu zero sau unu). Asadar, x = 3x₁, y = 3y₁. Prin urmare

In acelas timp, z² + t² < x² + y². Contradictia obtinuta demonstreaza justetea afirmatiei initiale.

Exemplul 4. In plan este data multimea de puncte M. Fiecare punct din M este mijlocul unui segment, ce uneste alte doua puncte din M. Sa se demonstreze ca multimea M este infinita.

Rezolvare. Admitem contrariul - multimea M este finita. Consideram in plan un sistem cartezian de coordonate. Fie un punct din M cu abscisa maximala (daca asa puncte sunt mai multe - alegem acel punct care are ordonata maximala). Notam acest punct prin A(x,y), el este mijlocul unui segment ce uneste punctele B(x₁,y₁) si C(x₂,y₂) din M. Din realatiile , x₁ ≤ x, x₂ ≤ x rezulta x₁ = x₂ = x, adica punctele A, B, C au aceeasi abscisa. Prin urmare y₁ ≤ y, y₂ ≤ y. ceea ce este imposibil, deoarece , iar punctele A, B, C sunt distincte. Contrazicerea cu ipoteza, prin urmare multimea M este infinita.

Exemplul 5. Fiecare latura a unui patrulater este diametrul unui cerc. Sa se arate ca cercurile construite acopera patrulaterul.

Rezolvare.

Notam patrulaterul dat ABCD (pe desen el este convex, dar rezolvarea ramane valabila si in cazul unui patrulater neconvex). Fie M un punct arbitrar din interiorul patrulaterului. Consideram unghiul maximal dintre unghiurile ÐAMB, ÐBMC, ÐCMD, ÐDMA. Fie, de exemplu, acest unghi ÐAMB. Atunci ÐAMB ≥ 90° (in caz contrar ÐAMB + ÐBMC + ÐCMD + ÐDMA < 4·90° = 360°). Prin urmare, punctul M va fi acoperit de cercul, construit pe latura AB ca diametru.

Exemplul 6. Sa se arate, ca daca lungimile tuturor laturilor triunghiului sunt mai mici ca 1, atunci aria lui este mai mica decat .

Rezolvare.

Fie in triunghiul ABC ÐA este cel mai mic unghi. Atunci ÐA ≤ 60° si aria triunghiului se estimeaza astfel:

Exemplul 7. In plan sunt date n (n ≥ 3) drepte, neparalele doua cate doua, astfel incat, prin punctul de intersectie a oricaror doua drepte dintre acestea, trece inca o dreapta. Sa se arate, ca toate dreptele trec printr-un punct.

Rezolvare. Admitem contrariul, adica exista asa o dreapta din familia data si exista asa punct de intersectie a altor doua drepte, ce nu apartin ei. Consideram distanta minimala (nenula) de la punctele de intersectie a dreptelor pana la drepte. Fie aceasta distanta este cea de la punctul A pana la dreapta l. Prin punctul A trec cel putin trei drepte.

Vom nota punctele de intersectie ale acestor drepte cu dreapta l prin B, C, D si vom cobora perpendiculara AP pe dreapta l. Cel putin doua dintre punctele B,C,D se afla de o parte in raport cu punctul P. Fie aceste puncte C si D, si PC < PD. Din punctele P si C coboram perpendicularele PQ si CR pe dreapta AD. Deoarece AP > PQ (ipotenuza triunghiului dreptunghic APQ este mai mare decat cateta) si PQ ≥ CR, rezulta AP > CR. Contradictie.

Exemplul 8. In plan sunt situate n (n ≥ 3) puncte astfel incat aria oricarui triunghi cu varfurile in aceste puncte nu intrece 1. Sa se arate ca toate punctele pot fi inchise intr-un triunghi de aria 4.

Rezolvare.

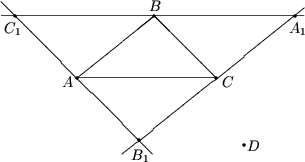
Consideram triunghiul de arie maxima cu varfurile in punctele date, fie acest triunghi - ABC. Prin punctele A, B, C ducem dreptele l_A, l_B, l_C, paralele cu laturile BC, CA, AB respectiv. Notam triunghiul format de dreptele l_A, l_B, l_C prin A₁B₁C₁. Aria acestui triunghi este de 4 ori mai mare decat aria triunghiului ABC, deci ea nu intrece 4.

Vom arata ca fiecare din punctele date se contine in triunghiul A₁B₁C₁. Admitem contrariul, adica exista un punct D din multimea data de puncte, ce se afla de parti diferite cu unul din varfurile A₁B₁C₁ relativ la latura opusa acestui varf. Fie, de exemplu, punctele C₁ si D se afla de parti diferite relativ la latura B₁A₁. Atunci distanta de la punctul D pana la AB este mai mare decat distanta de la punctul C pana la AB. Prin urmare, aria triunghiului ABD intrece aria triunghiului ABC, ceea ce contrazice alegeriea triunghiului ABC.

Exemplul 9. Sa se demonstreze, ca orice poligon convex de aria unu, poate fi inclus intr-un dreptunghi de aria doi.

Rezolvare.

Fie AB diagonala maximala a poligonului. Prin punctele A si B ducem perpendiculare la segmentul AB. Din alegerea segmentului AB rezulta ca tot poligonul se contine in fasia formata de aceste perpendiculare. Ducem dreptele CD, EF, paralele la AB prin unele varfuri ale poligonului in conditie ca poligonul se afla de o singura parte in raport cu fiecare dintre aceste drepte. Din punctele P si Q coboram perpendicularele PP₁ si QQ₁ pe AB. Aria poligonului initial este mai mare sau egala ca suma ariilor triunghiurilor APB si AQB, adica este nu mai mica decat

De aici rezulta, ca aria dreptunghiului EFDC, ce contine poligonul dat, nu intrece 2 (un.arie).

Exemplul 10. In plan sunt date patru puncte necoliniare. Sa se arate, ca cel putin un triunghi cu varfurile in aceste puncte nu este ascutitunghic.

Rezolvare.

Consideram un triunghi arbitrar cu varfurile in aceste puncte. Dreptele, construite pe laturile acestui triunghi impart planul in 7 parti. Apar urmatoarele cazuri:

I caz

Al patrulea punct este situat pe una din aceste drepte. In asa caz trei, fie punctele A, B, C, formeaza triunghiul, iar al patrulea punct, fie D, se afla pe una din laturi. Evident, cel mai mare dintre unghiurile ÐADB, ÐCDB nu este ascutit. Prin urmare, cel putin unul dintre triunghiurile ADB, CDB nu este ascutiunghic.

Cazul II.

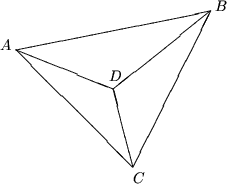
Al patrulea punct se afla in una din partile 2,4,6,7. In asa caz exista asa un triunghi ABC cu varfurile in punctele date si care contine in interiorul sau punctul D. Cel mai mare dintre unghiurile ÐADC, ÐCDB, ÐBDA, este nu mai mic de 120°, prin urmare cel putin unul dintre triunghiurile ADC, CDB, BDA, nu este ascutitunghic.

Cazul III.

Al patrulea punct se afla in una din partile 1,3,5. In asa caz cele patru puncte sunt varfurile unui patrulater convex ABCD. Cel mai mare dintre unghiurile ÐABC, ÐBCD, ÐCDA, ÐDAB este mai mare sau egal cu 90°. Prin urmare cel putin unul dintre triunghiurile ABC, BCD, CDA, DAB nu este ascutitunghic.

Exemplul 11. Sapte ciupercari au strans impreuna 100 de ciuperci, dar oricare doi din ei n-a strans acelasi numar de ciuperci. Sa se demonstreze, ca sunt trei ciupercari, ce au cules impreuna nu mai putin de 50 ciuperci.

Rezolvare. Consideram trei ciuperci ce au strans impreuna numarul maximal de ciuperci (dintre toate tripletele posibile de ciupercari). Daca numarul minimal de ciuperci stranse (dintre acesti trei ciupercari alesi) este 16, atunci impreuna ei au strans cel putin 16+17+18=51 ciuperci.

Daca numarul minimal indicat este mai mare decat 15, atunci cei patru ciupercari ramasi au strans cel mult 14+13+12+11=50. Prin urmare, si in acest caz primii trei au strans nu mai putin de 50 de ciuperci.

Exemplul 12. Elementele unui tabel n×n sunt zerouri si unitati. Tabelul este completat astfel incat daca la intersectia unei linii si coloane se afla un zerou, atunci suma elementelor de pe linia si coloana ce contin acest zerou este nu mai mica decat n. Sa se demonstreze ca suma celor n² numere din tabel nu este mai mica decat .

Rezolvare. Consideram coloana (linia) ce contine suma minimala a elementelor ei. Fie aceasta suma egala cu k. Daca , atunci sumele elementelor celorlalte coloane (linii) nu este mai mica ca si, prin urmare, suma tuturor elementelor nu este mai mica ca . Fie . Atunci in aceasta coloana (linie) sunt n - k zerouri. Prin urmare, suma elementelor fiecarei linii (coloane), ce contine un zerou din cele indicate este nu mai mica decat n - k. Asa coloane sunt n - k, prin urmare suma elementelor lor este nu mica decat (n - k)². Suma elementelor in cele k linii (coloane) ramase nu este mai mica decat k, si prin urmare, suma elementelor lor este mai mare sau egala cu k². Asadar, suma tuturor elementelor este nu mai mica decat

Exercitii pentru recapitulare

Sa se demonstreze ca multimea numerelor simple de forma 6m + 5, m Î N, este infinita.
Sa se arate, ca pentru orice numar natural n, n > 1, numarul nu este intreg.
Sa se demonstreze, ca ecuatia x² + y² + z² = 2¹⁹⁹⁹ nu are solutii in numere intregi.
Intr-o tara sunt 100 de aeroporturi si distanta dintre oricare doua din ele este diferita. Din fiecare port decoleaza un avion si zboara spre cel mai apropiat de el port. Sa se demonstreze ca nici intr-un port nu pot ateriza mai mult de 5 avioane.
In plan este data o multime finita de puncte. Orice dreapta ce trece prin doua din punctele date, contine inca un punct din multimea data. Sa se arate, ca toate punctele date se afla pe o dreapta.
Lungimile bisectoarelor unui triughi nu intrece 1cm. Demonstrati ca aria lui nu intrece .
Sa se demonstreze ca intr-un pentagon convex exista trei diagonale, din care se poate forma un triunghi.