Sa consideram urmatoarea problema.
Problema 1. Intr-o padure de conifere cresc 800000 de brazi. Fiecare brad are cel mult 500000 de ace. Sa se demonstreze, ca exista cel putin doi brazi cu acelasi numar de ace.
Solutie. Presupunem contrariul, adica presupunem ca nu exista doi brazi din aceasta padure cu un numar egal de ace. Atunci cel mult un brad (un brad sau nici unul) va avea un ac. La fel, cel mult un brad va avea doua ace, s.a.m.d, cel mult un brad va avea 499999, cel mult un brad va avea 500000 ace. Deci, cel mult 500000 au un numar de ace intre 1 si 500000. Cum in total sunt 800000 brazi, si deoarece fiecare brad are cel mult 500000 ace, rezulta ca vor fi cel putin doi brazi cu acelasi numar de ace.
Observatie. Se observa cu usurinta, ca solutia nu tine esential de numerele concrete 800000 (numarul de copaci) si 500000 (numarul maximal de ace). Principial a fost utilizat faptul, ca 800000 este strict mai mare decat 500000. In demonstratie s-a presupus ca nu exista brad fara ace, desi problema si demonstratia este adevarata si in acest caz.
Acum sa formulam principiul Dirichlet.
Fie in n cutii sunt plasate k obiecte. Daca obiecte sunt mai multe decat cutii (k > n), atunci exista cel putin o cutie care contine cel putin doua obiecte.
Nota. Mentionam, ca nu tinem cont de faptul care cutie contine cel putin doua obiecte. La fel nu este important cate obiecte sunt in aceasta cutie, precum si cate asa cutii avem. Este important ca exista cel putin o cutie cu cel putin doua obiecte (doua sau mai multe).
In literatura acest principiu poate fi intalnit si cu denumirile: "principiul sertarelor si obiectelor", "principiul iepurilor si custilor" etc.
Revenim din nou la problema 1. Sa rezolvam aceasta problema utilizand principiul Dirichlet. Fie avem 500000 cutii numerotate respectiv 1,2,3,...,500000. Plasam (virtual) in aceste cutii 800000 brazi in modul urmator: in cutia cu indicile s se repartizeaza brazii cu s ace. Deoarece brazi, adica "obiecte", sunt mai multe decat cutii, rezulta ca cel putin o cutie va contine cel putin doua obiecte, adica cel putin doi brazi. Deoarece in una si aceeasi cutie sunt brazi cu numar egal de ace, deducem ca exista cel putin doi brazi cu acelasi numar de ace.
Desigur problema 1 fiind evidenta, dupa cum s-a vazut, usor poate fi rezolvata si fara principiul Dirichlet. Astfel, natural apare intrebarea: "Pentru ce mai este nevoie de principiul Dirichlet?" In cele ce urmeaza vom vedea ca unele probleme nu sunt atat de evidente la solutionarea directa, si totodata suficient de simplu se rezolva utilizand principiul Dirichlet. Simplitatea rezolvarii in mare masura depinde de faptul pe cat de reusit vor fi alese "cutiile" si "obiectele". Deci, pentru aplicarea principiului Dirichlet este necesar de indicat cine (ce) sunt "cutiile" si cine (ce) sunt "obiectele".
Pentru consolidarea cunostintelor in continuare vom da rezolvarii o serie de probleme.
Problema 2. Sa se demonstreze, ca printre orice sase numere intregi exista doua numere diferenta carora este divizibila prin 5.
Solutie. Consideram 5 cutii etichetate cu numerele 0,1,2,3,4, care reprezinta resturile impartirii la 5. Repatizam in aceste cutii sase numere intrgi arbitrare, in dependenta de restul impartirii la 5, adica in aceasi cutie se plaseaza numerele cu acelasi rest de impartire la 5. Cum numere ("obiecte") sunt mai multe decat cutii, conform principiului Dirichlet, exista o cutie ce contine mai mult decat un obiect. Deci, exista (cel putin) doua numere plasate in aceeasi cutie. Prin urmare, exista doua numere cu acelasi rest de impartire prin 5. Atunci, diferenta lor este divizibila prin 5.
Problema 3. Sa se demonstreze ca pentru orice numar natural n ³ 1, exista un numar natural format din cifrele 0 si 5, divizibil prin n.
Solutie. Consideram numerele naturale
Daca in cutia cu indicile 0 este un "obiect" (adica un numar), atunci problema este rezolvata. In caz contrar n "obiecte" sunt plasate in n-1 "cutii". In baza principiului Dirichlet exista doua "obiecte" (numere) plasate in aceeasi cutue. Deci, exista doua numere cu acelasi rest la impartirea prin n. Diferenta lor va fi divizibila prin n si, cum usor se observa diferenta numerelor formate din cifrele 0 si 5 la fel va fi un numar format din cifrele 0 si 5.
Problema 4. Intr-o sala sunt n persoane (n ³ 2). Sa se demonstreze ca printre ei se vor gasi doi oameni cu acelasi numar de cunoscuti (se presupune ca daca persoana A este cunoscut al lui B, atunci si B este cunoscut al lui A; nimeni nu este considerat fiind cunoscut al lui insusi).
Solutie. Desemnam prin m numarul persoanelor ce au cel putin o cunostinta in sala (acestea si vor fi "obiectele"). Fiecare dintre aceste m persoane poate avea 1,2,...,m-1 cunoscuti ("cutiile" vor fi numarul de cunostinte).
Conform principiului Dirichlet exista doua persoane cu acelasi numar
de cunoscuti.
La rezolvarea unor probleme este util de aplicat principiul Dirichlet generalizat.
Daca plasam pn+1 obiecte in n cutii, atunci cel putin
o cutie va contine cel putin "p+1" obiecte.
Problema 5. Intr-o clasa sunt 40 elevi. Exista oare asa o luna a anului, in care cel putin 4 elevi sarbatoresc ziua sa de nastere.
Solutie. Fie "cutiile" sunt lunile anului si "obiectele" sunt elevii. Repartizam "obiectele" in "cutii" in dependenta de luna de nastere. Asa cum luni, adica cutii, sunt 12, iar elevi, adica obiecte 40 = 12·3+4, conform criteriului Dirichlet exista o cutie (o luna) cu cel putin 3+1=4 obiecte.
Problema 6. Fie M o multime formata din n numere intregi. Sa se demonstreze, ca exista o submultime a lui M, astfel incat suma elementelor sale este divizibila prin n.
Solutie. Fie M = {a1,a2,...,an}. Consideram urmatoarele sume:
| S1 = a1, |
| S2 = a1 + a2, |
| ... |
| Sn = a1 + a2 + ... + an. |
Daca unul din numerele Sk (k = 1,...,n) este divizibil prin n, atunci problema este rezolvata.
Daca nici unul din numerele Sk (k = 1,...,n) nu este divizibil prin n, atunci resturile lor la impartirea prin n vor fi 1,2,...,n - 1. Cum sunt n numere si n - 1 resturi, atunci cel putin doua vor da la impartirea prin n acelasi rest. Fie Sk si Sm (1 £ k < m £ n) doua dintre acestea. Atunci Sm - Sk se divide prin n si multimea cautata este {ak+1, ... ,am}.
Problema 7. Sa se demonstreze ca dintre n+1 numere naturale diferite mai mici ca 2n, pot fi extrase 3 numere, astfel incat un numar este egal cu suma celorlalte doua.
Solutie. Fie a1 < a2 < ... < an+1 sunt numerele date. Consideram diferentele
| a2 - a1, |
| a3 - a1, |
| ... |
| an+1 - a1. |
Aceste numere sunt pozitive, diferite si mai mici ca 2n. Astfel avem 2n + 1 numere naturale (a1,a2, ... ,an+1,a2 - a1, ... ,an+1 - a1), fiecare fiind mai mic ca 2n. Conform principiului Dirichlet cel putin doua numere coincid. Mai mult, unul dintre aceste doua numere apartine multimii a1,a2, ... ,an+1, si celalalt multimii a2 - a1, ... ,an+1 - a1. Fie aceste numere ak si am - a1. De aici ak = am - a1 si, deci am = ak + a1.
Problema 8. Fie a1,a2, ... ,an o permutare a numerelor 1,2,3,...,n. Sa se demonstreze, ca produsul (a1 - 1)(a2 - 2)...(an - n) este par daca n este impar.
Solutie. Fie n = 2k + 1. In multimea de numere considerate vor fi k + 1 numere impare. In produsul dat printre descazuti si scazatori vor fi (k + 1) + (k + 1) = 2(k + 1) = n + 1 numere prime. Cum in produs sunt n factori, unul din ei (cel putin) contine numai numere impare (si descazutul si scazatorul sunt numere impare). Astfel, acel factor este par, deci si produsul este par.
Problema 9. In 500 cutii se afla mere. Se stie ca in fiecare cutie se afla cel mult 240 mere. Sa se demonstreze ca exista cel putin 3 cutii ce contin acelasi numar de mere.
Solutie. Fie ca in primele 240 cutii se afla un numar diferit de mere (1,2,...,240) si in urmatoarele 240 de cutii la fel (adica se examineaza cazul extremal; despre aceasta metoda mai detaliat a se vedea tema "Principiul extremal"). Astfel au ramas 500 - 2·240 = 20 cutii, in care trebuie de plasat mere de la 1 la 240.
Problema 10. Intr-o cutie sunt 10 creioane de culoare rosie, 8 de culoare albastra, 8 de culoare verde si 4 de culoare galbena. La intamplare (aleator) din cutie se extrag n creioane. Sa se determine numarul minimal de creioane care trebuie de extras, astfel incat sa fie:
- a)
- nu mai putin de 4 creioane de aceeasi culoare;
- b)
- cate un creion de fiecare culoare;
- c)
- cel putin 6 creioane sunt de culoare albastra
Solutie. a) Fie ca sunt extrase 13 creioane. Deoarece culori sunt 4, conform principiului Dirichlet (creioanele sunt "obiectele", culorile sunt "cutiile") cel putin 4 creioane sunt de aceasi culoare. Sa demonstram ca n = 13 este numarul minimal. In acest scop, vom arata situatia in care conditiile problemei nu se realizeaza. De exemplu, atunci cand sunt extrase cate 3 creioane de fiecare culoare (12 creioane). Mentionam, ca aceasta situatie este posibila, deoarece exista cel putin 3 creioane de fiecare culoare.
Punctele b) si c) se rezolva similar.
Problema 11. La o intrunire internationala participa 17 persoane. Fiecare cunoaste cel mult trei limbi si oricare doi participanti pot conversa intre ei. Sa se demonstreze ca exista cel putin trei participanti care cunosc aceeasi limba.
Solutie. Fie A unul din participanti. El poate vorbi cu oricare din cei 16 participanti in cel mult o limba din cele trei. Atunci exista o limba, in care A vorbeste cu nu mai putin de 6 participanti. Printre acestea fie B unul oarecare. Este clar ca printre alti 5 participanti sunt 3 cu care B poate vorbi in aceeasi limba (o vom numi a doua limba). Daca printre acesti trei, cel putin doi, sa spunem C si D, pot vorbi cu oricare in a doua limba, atunci B, C si D sunt cei trei participanti ce vorbesc aceeasi limba.
Unele probleme (in special ce tin de geometrie) se rezolva, utilizand principiul Dirichlet in urmatoarele enunturi:
- a)
- Daca pe un segment de lungime l sunt situate cateva segmente cu suma lungimilor mai mare ca l, atunci cel putin doua segmente au un punct comun;
- b)
- Daca in interiorul unei figuri de arie S sunt plasate figuri cu suma ariilor mai mare decat S, atunci exista cel putin doua dintre aceste figuri cu un punct comun;
- c)
- Daca figurile F1,F2, ... ,Fn cu ariile S1,S2, ... ,Sn respectiv sunt incluse in figura F cu arie S si S1 + S2 + ... + Sn > kS, atunci k + 1 din figurile F1,F2, ... ,Fn au un punct comun.
Problema 12. Punctele planului sunt colorate in doua culori. Sa se arate ca exista doua puncte de aceeasi culoare situate la distanta 1m.
Solutie. Consideram un triunghi echilateral cu lungimea laturii de 1m. Varfurile triunghiului vor desemna "obiectele" si culorile vor fi "cutiile". Cum "obiecte" sunt mai multe decat "cutii" rezulta, ca exista doua varfuri de aceeasi culoare. Intrucat triunghiul este echilateral, distanta dintre varfuri este 1m.
Tinem sa mentionam ca aceasta problema poate fi rezolvata si prin alta metoda, si anume de la contrariu. Fie A un punct in plan si presupunem, ca toate punctele din plan situate la distanta de 1m de A sunt de culoare diferita de culoarea punctului A. Atunci avem o circumferinta de raza 1 din puncte de aceeasi culoare. Evident exista o coarda a acestei circumferinte de lungime 1m. Prin urmare, extremitatile coardei sunt puncte de aceeasi culoare situate la distanta de 1m.
Problema 13. Se considera in plan n puncte distincte. Cate doua puncte determina un segment. Sa se demonstreze ca exista doua puncte din care pleaca acelasi numar de segmente.
Solutie. Dintr-un punct pleaca maximum n - 1 segmente si minim 1. Cum avem n puncte, vor exista doua din care pleaca acelasi numar de segmente.
Problema 14. In interiorul patratului de latura 1 sunt asezate cateva cercuri, avand suma lungimilor egala cu 10. Sa se arate ca exista o dreapta, care sa intersecteze cel putin patru din aceste cercuri.
Solutie. Se proiecteaza cercurile pe una din laturile patratului.
Proiectia fiecarui cerc este un segment cu lungimea egala cu lungimea
diametrului cercului respectiv. Suma tuturor acestor segmente este
![]() Conform principiului Dirichlet, exista cel putin patru segmente ce au in
comun un punct. Perpendiculara ridicata in acest punct, pe latura patratului,
va intersecta cel putin patru cercuri.
Conform principiului Dirichlet, exista cel putin patru segmente ce au in
comun un punct. Perpendiculara ridicata in acest punct, pe latura patratului,
va intersecta cel putin patru cercuri.
Problema 15. In interiorul unui triunghi echilateral cu lungimea laturii 1 sunt plasate 5 puncte. Sa se demonstreze ca exista doua puncte din cele 5 cu distanta intre ele mai mica decat 0,5.
Solutie. Divizam triunghiul echilateral cu latura 1 in patru triunghiuri echilaterale cu lungimea laturii de 0,5 (fig. 1).

In unul dintre aceste patru triunghiuri sunt cel putin doua puncte din cele date. Distanta dintre aceste doua puncte este mai mica decat 0,5.
Problema 16. In plan sunt date 25 puncte, astfel incat dintre orice trei puncte doua puncte sunt situate la distanta mai mica ca 1. Sa se demonstreze ca exista un cerc de raza 1 ce contine nu mai putin de 13 din aceste puncte.
Solutie. Fie A unul din punctele date. Daca celelalte puncte sunt in interiorul cercului S1 de raza 1 si centrul in A, atunci problema este solutionata. Fie B unul dintre punctele situate in exteriorul cercului S1. Examinam cercul S2 de raza 1 si centrul B. Printre punctele A, B, C, unde C un punct arbitrar dintre cele date, exista doua cu distanta intre ele mai mica decat 1. Mai mult aceste puncte nu pot fi A si B. Astfel cercurile S1 si S2 contin toate punctele initiale. Deci, unul dintre aceste cercuri contine cel putin 13 puncte.
Problema 17. In plan se considera n drepte neparalele doua cate
doua. Sa se arate ca exista drepte cu unghiul intre ele mai mic decat
![]()
Solutie. Se alege un punct in plan prin care se duc drepte paralele
la cele n drepte. Aceste drepte impart planul in 2n unghiuri cu suma
masurilor egale cu 360°. Deci cel, putin unul din unghiuri este
mai mic decat ![]()
Problema 18. Pe o retea infinita este plasata o figura de arie mai mica decat aria unui patratel al retelei. Sa se demonstreze, ca aceasta figura poate fi plasata pe retea astfel incat nu va acoperi un nod al retelei.
Solutie. Plasam figura data in mod arbitrar peste retea si taiem reteaua de-a lungul laturilor. Aranjam toate patratele unul peste altul formand un fisic, efectuand numai translatii paralele (fara a intoarce). Proiectam fisicul pe un patratel. Proiectiile figurii nu pot acoperi intregul patratel, deoarece aria figurii este mai mica decat aria patratulului. Revenim la pozitia initiala a figurii si translam paralel reteaua, astfel incat proiectiile varfurilor sa fie in puncte neacoperite de proiectiile figurii. Ca rezultat vom obtine pozitia figurii.
- Sa se demonstreze ca din 11 cifre pot fi selectate doua cifre identice.
- Sa se arate ca din 3 numere nenule 2 sunt de acelasi semn.
- Sa se demonstreze, ca intr-o scoala cu 400 elevi exista doi elevi cu ziua de nastere in aceasi zi a anului.
- Sa se demonstreze, ca exista un numar de forma
1999 1999... 1999 00... 00, divizibil prin 1999. - Sa se demonstreze, ca orice multime formata din 2n+1 - 1 numere intregi contine o submultime formata din 2n numere, suma carora este divizibila prin 2n.
- Sa se arate ca exista un numar natural cu ultimele patru cifre 1998 si divizibil prin 1997.
- In campionatul national de fotbal participa 30 echipe. Sa se demonstreze, ca in orice moment exista doua echipe cu numar egal de jocuri jucate in campionat.
- Sa se arate, ca printre orice (n + 2) numere naturale exista doua numere cu suma sau diferenta divizibila prin 2n.
- Sa se arate, ca printre n + 1 numere naturale mai mici decat 2n, exista doua avand raportul o putere a lui 2.
- Sa se arate, ca din orice trei numere prime, mai mari decat 3, se pot alege doua cu proprietatea ca suma sau diferenta lor se divide cu 12.
- Sa se arate, ca orice ar fi numerele intregi a, b, c, d numarul
abcd(a2 - b2)(a2 - d2)(b2 - c2)(b2 - d2)(c2 - d2) este multiplu de sapte. - Sa se demonstreze, ca pentru orice numar natural exista un multiplu al lui scris numai cu cifrele 0 si 1.
- Fie n Î N, n > 1. Sa se arate ca oricum am alege n + 2 numere din multimea {1,2,...,3n}, printre ele exista doua cu diferenta situata in intervalul (n,2n).
- Nodurile unei retele infinite sunt vopsite in doua culori. Sa se demonstreze, ca exista doua drepte verticale si doua drepte orizontale, intersectia carora contine puncte de aceeasi culoare.
- In dreptunghiul 3×4 sunt plasate 6 puncte. Sa se demonstreze,
ca printre aceste puncte exista doua cu distanta dintre ele mai mica
decat
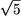 .
.
- Intr-un patrat cu lungimea laturii 1 sunt plasate 51 puncte. Sa se demonstreze ca trei din aceste puncte pot fi acoperite cu un cerc de raza 1/7.
- Sa se arate ca in orice poligon convex cu 2n laturi, exista o diagonala neparalela cu nici una din laturi.
- Sa se determine numarul minimal de puncte necesare de marcat in interiorul unui poligon convex cu n laturi, astfel incat orice triunghi cu varfurile in varfurile poligonului sa contina cel putin un punct marcat.
- Intr-un cerc de raza 1 sunt trasate cateva coarde. Sa se demonstreze, ca daca fiecare diametru intersecteaza nu mai mult de S coarde, atunci suma lungimilor coardelor este mai mica decat pS.
- Intr-un cerc de raza 16 sunt plasate 650 puncte. Sa se arate, ca exista un inel cu raza mare 3 si raza mica 2, care contine mai mult de 10 puncte de cele date.
- Sa se arate ca nu se pot vopsi fetele unui cub, folosind numai doua culori, astfel incat oricare doua fete vecine sa aiba culori diferite.
- Fie m3 + 1 puncte plasate intr-un cub cu latura de lungimea 1. Sa se
arate ca exista cel putin doua puncte astfel incat distanta intre ele
sa fie mai mica decat

- Sa se arate, ca in fiecare poligon cu noua laturi exista o pereche de diagonale cu unghiul intre ele mai mic decat 7°.
- Sunt date doua cercuri fiecare de lungime 100cm. Pe un cerc (circumferinta) sunt marcate 100 puncte, iar pe celalalt sunt marcate cateva arcuri cu suma lungimilor mai mica decat 1. Sa se demonstreze, ca aceste cercuri pot fi suprapuse astfel incat nici unul dintre punctele marcate nu va nimeri pe arcurile marcate.
- Mircea Ganga, Teme si probleme de matematica, Ed. Tehnica, Bucuresti, 1991, 331p.
- V.A.Ufnarovski, Acvariu Matematic, "Stiinta", Chisinau, 1988, 237p.
- V.V.Prasolov, Zadaci po planimetrii, c.2, Moskva, Nauka, 1991, 139str. (rus.)
- I.L.Babinskaya, Zadaci matematiceskih olimpiad, Nauka, Moskva, 1975, 112str. (rus.)
- V.A.Gusev, A.I.Orlov, A.L.Rozental, Lucrul in afara orelor de curs la matematica in clasele VI-VIII, Chisinau, Lumina, 1980, 293p.